数据结构——矩阵压缩
特殊矩阵的压缩
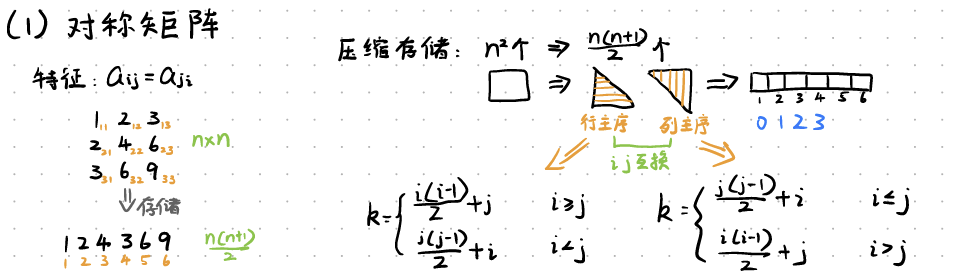
对称矩阵
关键点:
是选择上三角行主序存储还是下三角列主序存储
组的下标是从1开始还是0开始存储
image-20241019163345497
image-20241019163357393
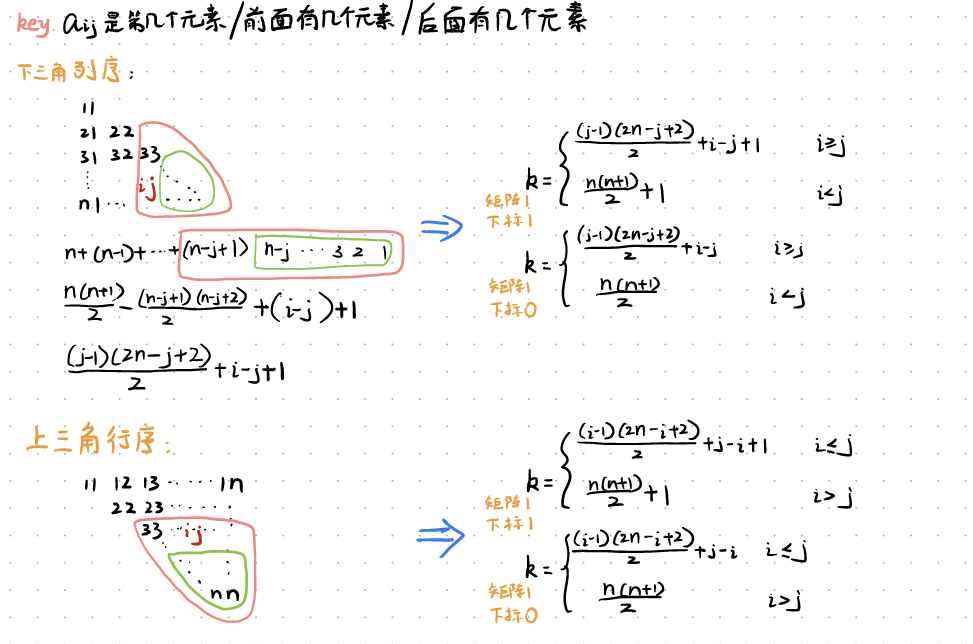
三件矩阵
注意点:
image-20241019162703259
image-20241019162719970
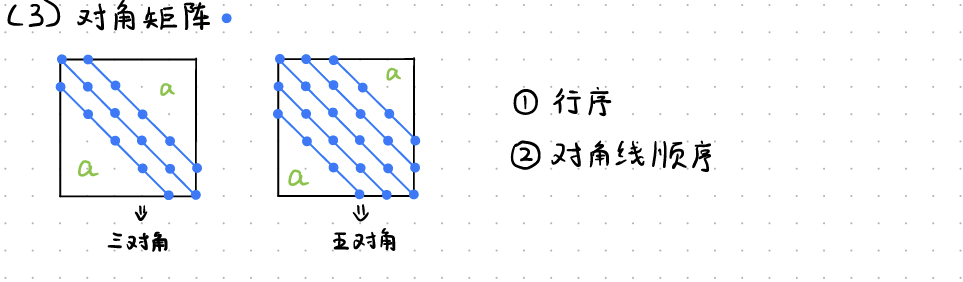
对角矩阵
image-20241019163805806
稀疏矩阵的压缩存储
三元组表
IMG_20241019_164539
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 struct Triplet { int row; int col; int value; }; class SparseMatrix {private : int rows; int cols; vector<Triplet> triplets; public : SparseMatrix (int rows, int cols) : rows (rows), cols (cols) {} void add_element (int row, int col, int value) if (value != 0 ) { triplets.push_back ({ row, col, value }); } } void display () const for (const auto & triplet : triplets) { cout << "行: " << triplet.row << ", 列: " << triplet.col << ", 值: " << triplet.value << endl; } } vector<vector<int >> to_dense () const { vector<vector<int >> dense_matrix (rows, vector <int >(cols, 0 )); for (const auto & triplet : triplets) { dense_matrix[triplet.row][triplet.col] = triplet.value; } return dense_matrix; } };
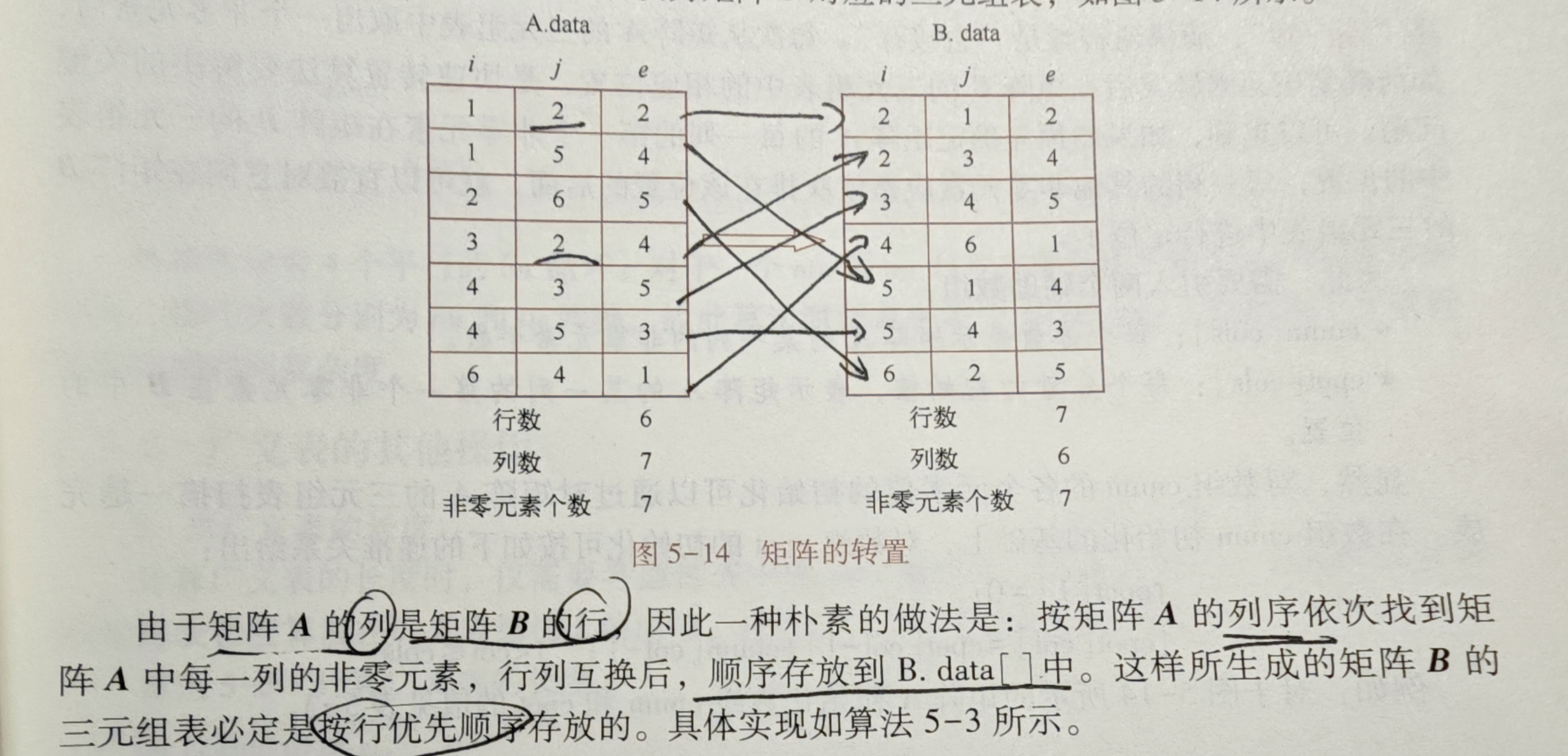
朴素转置
IMG_20241019_181951
因为矩阵A的列是矩阵B的行,所以以此遍历A的列,将其存入新的三元组顺序表
不能直接交换i和j的值的原因:因为三元组表是行优先顺序,如果直接交换就是列优先
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 vector<Triplet> transposeTripletMatrix (const vector<Triplet>& tripletMatrix) { int rows = tripletMatrix[0 ].row; int cols = tripletMatrix[0 ].col; int numNonZero = tripletMatrix[0 ].value; vector<Triplet> transposedMatrix; transposedMatrix.push_back ({cols, rows, numNonZero}); if (numNonZero > 0 ) { for (int col = 0 ; col < cols; ++col) { for (int i = 1 ; i <= numNonZero; ++i) { if (tripletMatrix[i].col == col) { transposedMatrix.push_back ({tripletMatrix[i].col, tripletMatrix[i].row, tripletMatrix[i].value}); } } } } return transposedMatrix; }
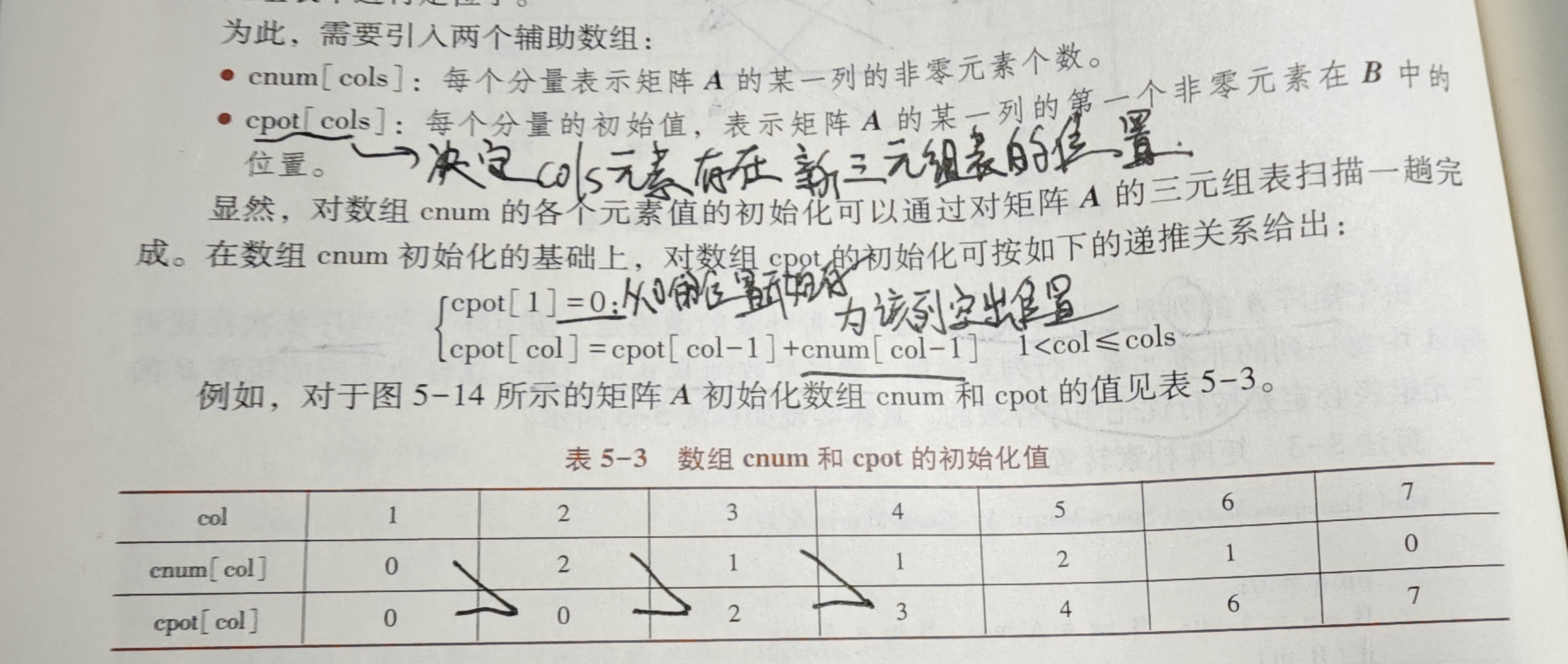
快速转置
IMG_20241019_235512
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 vector<Triplet> fastTransposeTripletMatrix (const vector<Triplet>& tripletMatrix) { int rows = tripletMatrix[0 ].row; int cols = tripletMatrix[0 ].col; int numNonZero = tripletMatrix[0 ].value; vector<Triplet> transposedMatrix (numNonZero + 1 ) ; transposedMatrix[0 ] = {cols, rows, numNonZero}; if (numNonZero > 0 ) { vector<int > count (cols, 0 ) ; vector<int > index (cols + 1 , 2 ) ; for (int i = 1 ; i <= numNonZero; ++i) { count[tripletMatrix[i].col]++; } for (int i = 1 ; i < cols; ++i) { index[i + 1 ] = index[i] + count[i - 1 ]; } for (int i = 1 ; i <= numNonZero; ++i) { int col = tripletMatrix[i].col; int pos = index[col]; transposedMatrix[pos] = {tripletMatrix[i].col, tripletMatrix[i].row, tripletMatrix[i].value}; index[col]++; } } return transposedMatrix; }
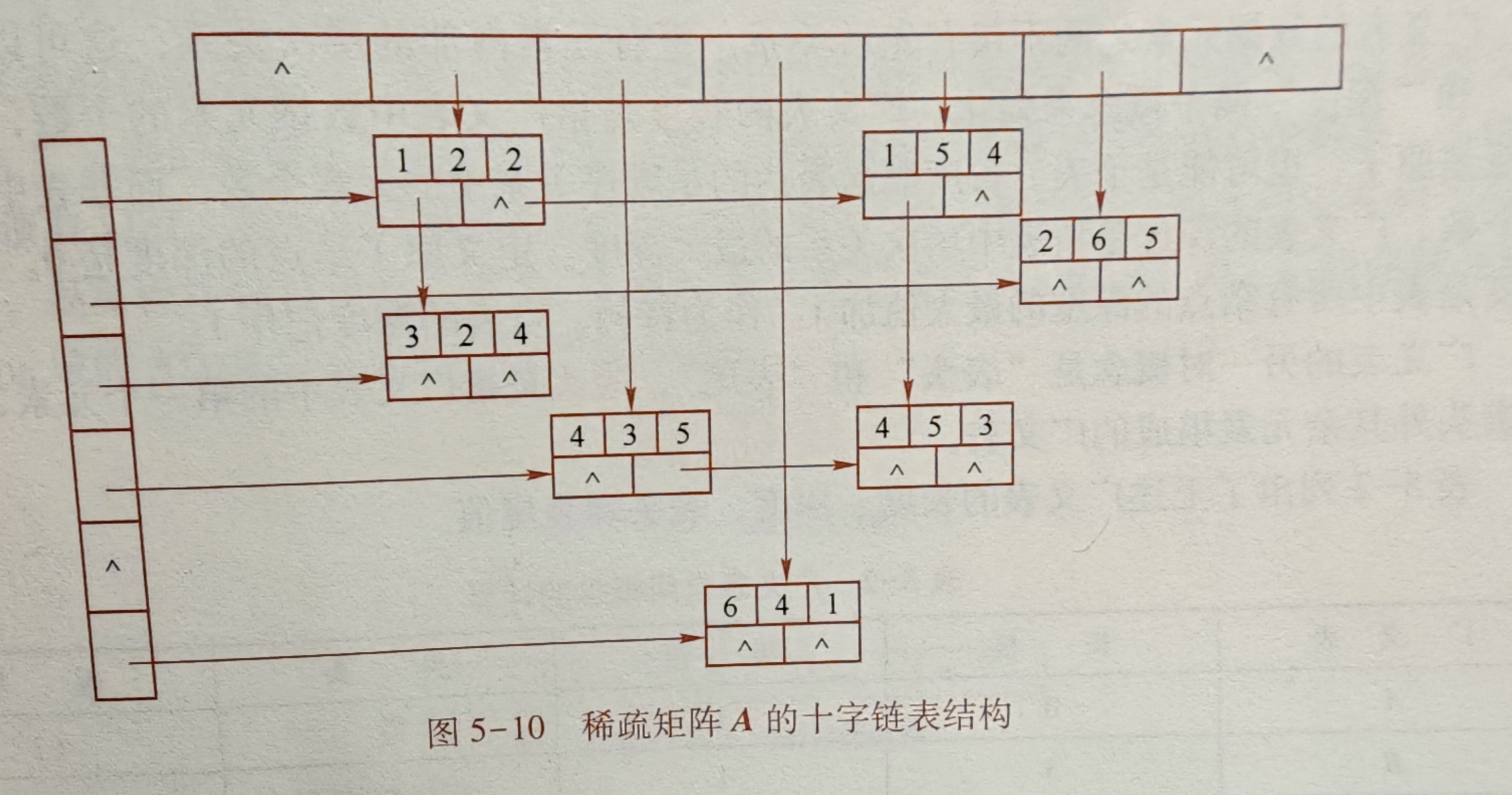
十字链表
IMG_20241019_170755
定义
类中定义了两个链表数组,用于存储每一行和每一列的头节点指针
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 struct OLNode { int row; int col; int value; OLNode* right; OLNode* down; OLNode (int r, int c, int val) : row (r), col (c), value (val), right (nullptr ), down (nullptr ) {} }; class OrthogonalList {private : int rows, cols; vector<OLNode*> row_heads; vector<OLNode*> col_heads; }
构造函数
row_heads.resize(rows, nullptr); 是用于调整
row_heads 向量的大小,使其包含 rows
个元素,并将每个元素初始化为 nullptr。
1 2 3 4 OrthogonalList (int rows, int cols) : rows (rows), cols (cols) { row_heads.resize (rows, nullptr ); col_heads.resize (cols, nullptr ); }
插入函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 void insert (int r, int c, int value) if (value == 0 ) return ; OLNode* current = row_heads[r]; while (current && current->col < c) { current = current->right; } if (current && current->col == c) { current->value = value; return ; } OLNode* newNode = new OLNode (r, c, value); if (!row_heads[r]) { row_heads[r] = newNode; } else { current = row_heads[r]; OLNode* prev = nullptr ; while (current && current->col < c) { prev = current; current = current->right; } if (prev) { prev->right = newNode; } else { row_heads[r] = newNode; } newNode->right = current; } if (!col_heads[c]) { col_heads[c] = newNode; } else { current = col_heads[c]; OLNode* prev = nullptr ; while (current && current->row < r) { prev = current; current = current->down; } if (prev) { prev->down = newNode; } else { col_heads[c] = newNode; } newNode->down = current; } }
打印函数
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void print () for (int i = 0 ; i < rows; ++i) { OLNode* current = row_heads[i]; for (int j = 0 ; j < cols; ++j) { if (current && current->col == j) { cout << current->value << " " ; current = current->right; } else { cout << "0 " ; } } cout << endl; } } };
参考文献
【数据结构】特殊矩阵的压缩存储/对称矩阵/三角矩阵/对角矩阵(含经典题讲解)_哔哩哔哩_bilibili
【每个人都听得懂的】稀疏矩阵的快速转置算法_哔哩哔哩_bilibili