数据结构——线性表

发表于 更新于 分类于 ， 阅读次数：

数据结构——线性表

线性表的定义

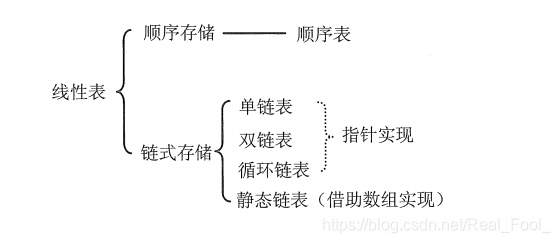
线性表（List）：零个或多个数据元素的有限序列。

c8b3abeb72098a922a9ac4f6ff62f563

顺序存储结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#ifndef SEQLIST_H
#define SEQLIST_H

#include <iostream>
using namespace std;

// 模板类定义，表示顺序表
template <class T, int MaxSize>
class SeqList {
    T data[MaxSize];  // 存储顺序表数据的数组
    int length;       // 顺序表的长度
public:
    
};

#endif

链式存储结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#ifndef LINKLIST_H
#define LINKLIST_H

#include <iostream>
using namespace std;

template <class T>
struct Node {
    T data;
    Node<T>* next;
};

template <class T>
class LinkList {
    Node<T>* head;

public:

};
#endif // LINKLIST_H

归并排序

[归并排序 | 菜鸟教程](https://www.runoob.com/data-structures/merge-sort.html#:~:text=归并排序（Merge sort）是建立在归并操作上的一种有效、稳定的排序算法，该算法是采用分治法 (Divide,and Conquer）的一个非常典型的应用。 将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。 若将两个有序表合并成一个有序表，称为二路归并。)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
// 友元函数：合并两个有序顺序表
template <class T, int MaxSize1, int MaxSize2>
SeqList<T, MaxSize1 + MaxSize2> Merge(const SeqList<T, MaxSize1>& list1, const SeqList<T, MaxSize2>& list2) {
    SeqList<T, MaxSize1 + MaxSize2> MergedList;  // 创建一个新的顺序表
    int i = 0, j = 0, n = 0;                    // 定义三个指针，分别表示 list1、list2 和合并表的当前索引

    // 获取两个顺序表的长度
    int length1 = list1.length;
    int length2 = list2.length;

    // 合并两个有序顺序表
    while (i < length1 && j < length2) {
        if (list1.data[i] <= list2.data[j]) {
            MergedList.data[n++] = list1.data[i++];
        }
        else {
            MergedList.data[n++] = list2.data[j++];
        }
    }

    // 将 list1 中剩余的元素插入到 MergedList 中
    while (i < length1) {
        MergedList.data[n++] = list1.data[i++];
    }

    // 将 list2 中剩余的元素插入到 MergedList 中
    while (j < length2) {
        MergedList.data[n++] = list2.data[j++];
    }

    MergedList.length = n;  // 设置合并后的顺序表长度
    return MergedList;
}