数据结构——树和二叉树

发表于 更新于 分类于 ， 阅读次数：

树

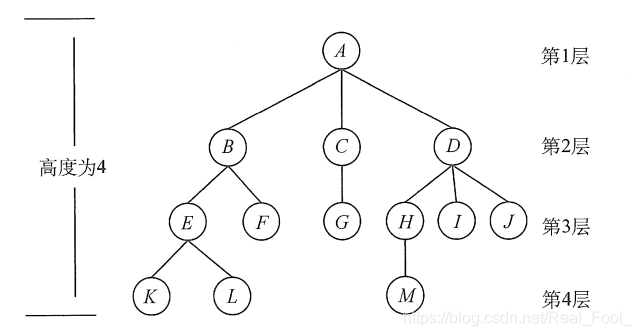
树的基本术语

d72517fa6b39dc28ff37c0942cda4df1

  1. 结点的度和树的度

    树中结点的最大度数称为树的度。如结点B的度为2,结点D的度为3,树的度为3。

  2. 孩子，双亲，兄弟结点

  3. 路径和路径长度

    树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的,而路径长度是路径上所经过的边的个数。 注意:由于树中的分支是有向的,即从双亲指向孩子,所以树中的路径是从上向下的,同一双亲的两个孩子之间不存在路径。

  4. 子孙结点和祖先结点

    根A到结点K的唯一路径上的任意结点,称为结点K的祖先。如结点B是结点K的祖先,而结点K是结点B的子孙。

  5. 结点的层次和树的高度

    结点的层次从树根开始定义,根结点为第1层,它的子结点为第2层,以此类推。

  6. 有序树和无序树

    树中结点的各子树从左到右是有次序的,不能互换,称该树为有序树,否则称为无序树。

  7. 森林

    森林是m (m≥0)棵互不相交的树的集合。

树的存储结构

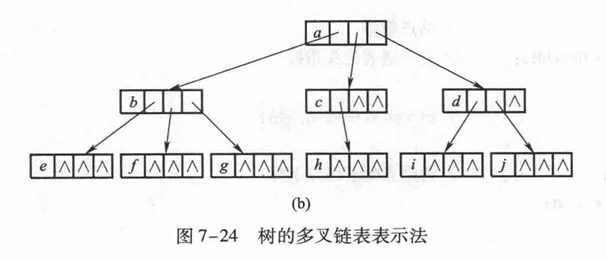
多叉链表表示法

fasdfa

采用多叉链表表示法存储树，许多算法设计可以直接参照二叉树的二叉链表结构的算法。其优点是简单易学，缺点是存在许多指针域的浪费。设树中结点数是n，树的度是k，则共使用了n×k个指针域，而这其中只有n -1个非空指针城。

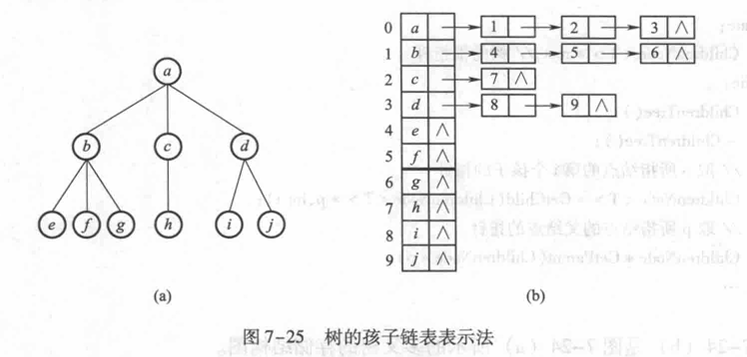
孩子链表表示法

safsafsxcx

当树的度较大时，CTree类可以减少多叉链表表示法的空间浪费。但是，当插入、删除结点时，却会涉及多个孩子链表的调整,还有可能造成存储空间的再分配，因此时间复杂度较大。在CTree类中，利用孩子链表可以方便、快捷地查找指定结点的孩子结点。但是，查找双亲结点则需遍历所有的孩子链表,因此效率就低得多了。

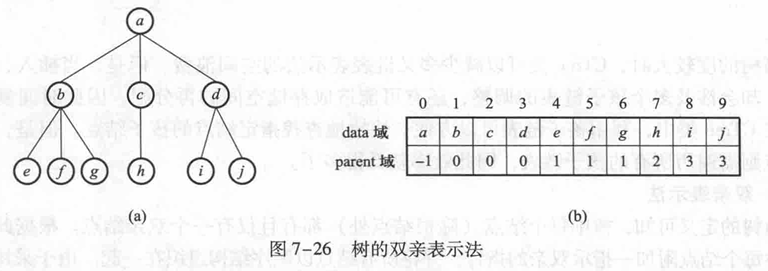
双亲表示法

sadfas

在PTree类中，不仅利用结点的双亲指针域很容易找到其双亲结点，而且查找其所有祖先结点也非常便利、高效。若需要查找指定结点的孩子或子孙结点，则需遍历整个树的存储空间，效率就低得多了。

孩子兄弟表示法

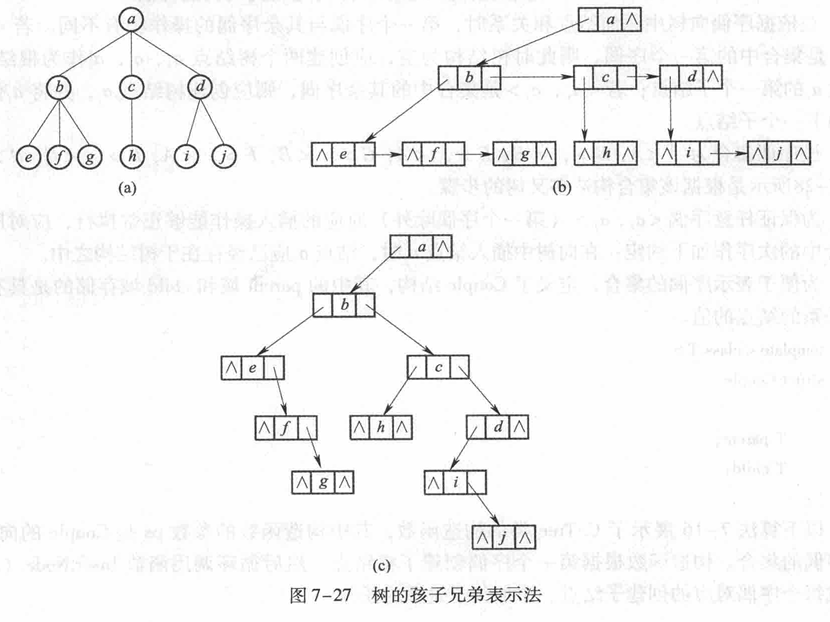dasfgae

因为孩子兄弟表示法建立起了树和二叉树之间的对应关系，所以常常将其称为树的二叉树表示法。相比树的其他存储结构，孩子兄弟表示法既简化了结构，又可以将许多二叉树的优秀算法移植到树结构的应用中来，因此具有很好的学习、应用价值。

树的操作算法

构造算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
// 构造函数
    CSTree(vector<pair<T, T>>& ps) {
        if (ps.empty()) {
            root = nullptr;
            return;
        }
        // 创建根节点
        root = new CSNode<T>(ps[0].first);
        root->firstchild = nullptr;
        root->nextsibling = nullptr;

        // 插入其他节点
        for (size_t i = 0; i < ps.size(); i++) {
            InsertNode(ps[i]);
        }
    }
// 插入节点
    void InsertNode(pair<T, T>& p) {
        // 创建新节点
        CSNode<T>* child = new CSNode<T>(p.second);
        child->firstchild = nullptr;
        child->nextsibling = nullptr;

        // 找到父节点
        CSNode<T>* parent = Search(root, p.first);
        if (!parent) {
            cout << "Parent node " << p.first << " not found!" << endl;
            return;
        }

        // 若父节点无子节点，将新节点作为第一个子节点
        if (parent->firstchild == nullptr) {
            parent->firstchild = child;
        } else {
            // 若父节点已有子节点，将新节点作为最后一个子节点
            CSNode<T>* temp = parent->firstchild;
            while (temp->nextsibling != nullptr) {
                temp = temp->nextsibling;
            }
            temp->nextsibling = child;
        }
    }

计算树的高度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 计算指定节点子树的高度
template <class T>
int CSTree<T>::Height(CSNode<T>* p) {
    if (p == nullptr)  // 如果节点为空，返回高度 0
        return 0;

    int maxheight = 0;  // 初始化子树的最大高度为 0

    // 遍历所有子节点
    for (CSNode<T>* child = p->firstchild; child != nullptr; child = child->nextsibling) {
        int height = Height(child);  // 递归计算子节点的高度
        if (height > maxheight)      // 更新最大高度
            maxheight = height;
    }

    return maxheight + 1;  // 当前节点的高度为子树最大高度 + 1
}

// 外部接口：计算整棵树的高度
template <class T>
int CSTree<T>::Height() {
    return Height(root);  // 从根节点开始计算高度
}

计算所有结点的度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 计算指定节点的度并递归处理其子树
template <class T>
void CSTree<T>::Degree(CSNode<T>* p) {
    if (p == nullptr)  // 如果节点为空，直接返回
        return;

    p->degree = 0;  // 初始化节点的度为 0

    // 遍历所有子节点，统计度
    for (CSNode<T>* child = p->firstchild; child != nullptr; child = child->nextsibling) {
        p->degree++;  // 子节点存在则度加 1
    }

    Degree(p->firstchild);    // 递归处理子节点的度
    Degree(p->nextsibling);   // 递归处理兄弟节点的度
}

// 外部接口：计算整棵树的所有节点的度
template <class T>
void CSTree<T>::Degree() {
    Degree(root);  // 从根节点开始计算度
}

二叉树

特殊的二叉树

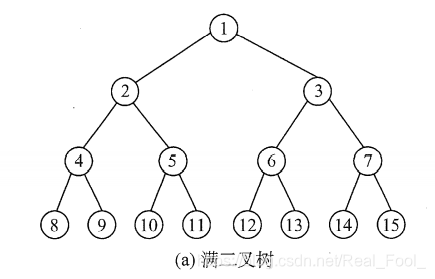3ca44306b6c5f97c3544f5d091be9ac4
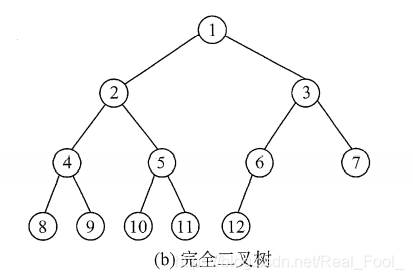a99ebdd407f8c2508597d85c610c44a7

二叉树的性质

非空二叉树上的叶子结点数等于度为2的结点数加1，即 n0 = n1 + 1

因为二叉树中所有节点的度只能是 0、1、2，所以节点总数  n = n0 + n1 + n2

其次考虑二叉树的分支总数。将二叉树的分支总数记作 m。 因为所有的分支是由度为 1 和度为 2 的节点发出的，所以m = n1 + 2 × n2

最后，由树的性质 1，可得 n = m + 1，即n0 + n1 + n2 = n1 + 2 × n2 + 1

二叉树的存储结构

顺序结构

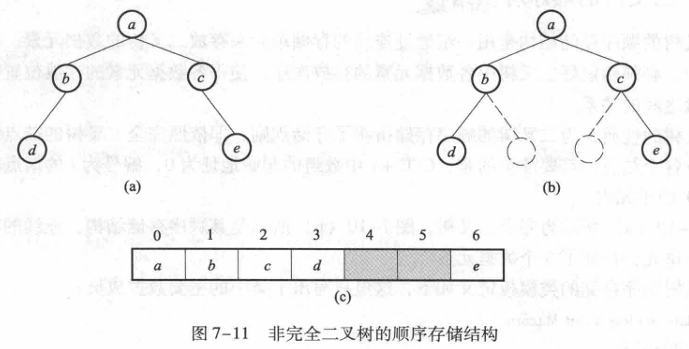afdfa

当二叉树单分支节点较多，高度变化较大时，空间浪费现象惊人

链式结构

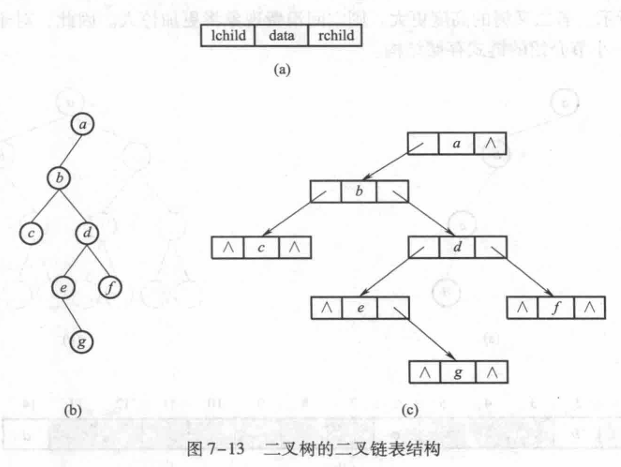adsfgad

二叉树的遍历

前序遍历：根左右

中序遍历：左根右

后序遍历：左右根

先序遍历算法如下

1
2
3
4
5
6
7
8
9
10
11
12
13
template <class T>
void BiTree<T>::PreOrder(BiNode<T>* p) {
    if (p == NULL)
        return;             // ① 若二叉树为空，则遍历结束
    cout << p->data;        // ② 访问当前结点
    PreOrder(p->lchild);    // ③ 先序遍历当前结点的左子树
    PreOrder(p->rchild);    // ④ 先序遍历当前结点的右子树
}

template <class T>
void BiTree<T>::PreOrder() {
    PreOrder(root);
}

层序遍历：利用队列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
template <class T>
void BiTree<T>::LevelOrder() {
    if (root == NULL)
        return;             // ① 若二叉树为空，则遍历结束

    LinkQueue<BiNode<T>*> Q;    // 定义一个队列存储节点指针
    Q.EnQueue(root);            // ② 将根指针加入指针队列

    while (!Q.Empty()) {        // ③ 若指针队列不空，则循环
        BiNode<T>* p = Q.DeQueue();   // ④ 出队列，得到当前指针 p
        cout << p->data;              // ④ 访问当前结点

        // ⑤ 若当前结点有左孩子，则左孩子地址进指针队列
        if (p->lchild != NULL)
            Q.EnQueue(p->lchild);

        // ⑤ 若当前结点有右孩子，则右孩子地址进指针队列
        if (p->rchild != NULL)
            Q.EnQueue(p->rchild);
    }
}

二叉树的构造算法

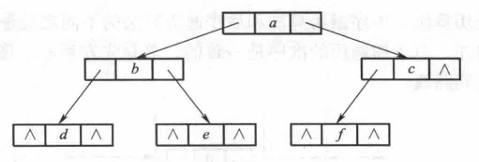sADF

先序序列是abdecf，带空指针标记的先序序列是abd**e**cf ***

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
template <class T>
BinNode<T>* BinTree<T>::CreateByPre(vector<T>& pre, int& i) {
    T e = pre[i]; // 提取当前数据
    i++;
    if (e == '*') // 若是特殊数据，返回空指针
        return NULL;

    // 创建新结点
    BinNode<T>* p = new BinNode<T>;
    p->data = e;
    // 创建左子树
    p->lchild = CreateByPre(pre, i);
    // 创建右子树
    p->rchild = CreateByPre(pre, i);

    return p;
}

template <class T>
BinTree<T>::BinTree(vector<T>& pre) {
    int i = 0; // 向量 pre 的下标变量
    root = CreateByPre(pre, i); // 从先序序列构造二叉树
}

二叉树的其他操作算法

计算结点数

1
2
3
4
5
6
7
8
9
10
11
12
13
template <class T>
int BiTree<T>::Count(BiNode<T>* p) {
    if (p == NULL)
        return 0;  // 当前节点为空，返回 0
    int left = Count(p->lchild);  // 统计左子树节点数
    int right = Count(p->rchild); // 统计右子树节点数
    return 1 + left + right;      // 当前节点总数 = 左子树 + 右子树 + 当前节点
}

template <class T>
int BiTree<T>::Count() {
    return Count(root); // 从根节点开始统计
}

计算高度

1
2
3
4
5
6
7
8
9
10
11
12
13
template <class T>
int BiTree<T>::Height(BiNode<T>* p) {
    if (p == NULL)
        return 0;  // 空节点高度为 0
    int left = Height(p->lchild);  // 左子树高度
    int right = Height(p->rchild); // 右子树高度
    return (left > right ? left : right) + 1; // 树高度为左右子树最大高度 + 1
}

template <class T>
int BiTree<T>::Height() {
    return Height(root); // 从根节点开始计算树高度
}

查找结点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
template <class T>
BinNode<T>* BiTree<T>::Search(BinNode<T>* p, T e) {
    if (p == NULL)
        return NULL;  // 查找失败
    if (p->data == e)
        return p;     // 查找成功，返回节点指针

    // 在左子树中递归查找
    BinNode<T>* q = Search(p->lchild, e);
    if (q != NULL)
        return q; // 若在左子树中找到，返回结果

    // 在右子树中递归查找
    return Search(p->rchild, e);
}

template <class T>
BinNode<T>* BiTree<T>::Search(T e) {
    return Search(root, e); // 从根节点开始查找
}

线索二叉树

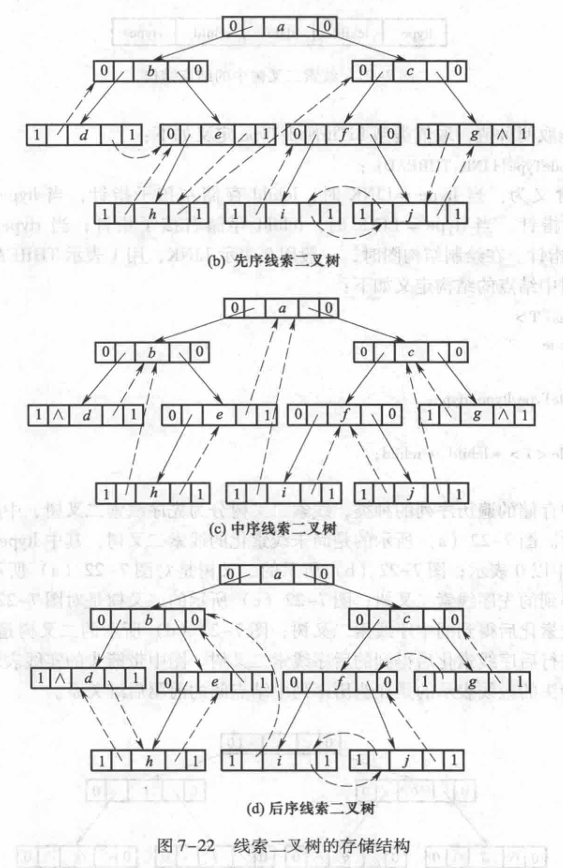asfafs

哈夫曼树

wqqwr
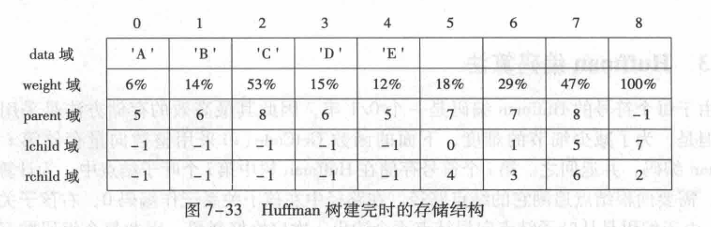qetqt

参考文献

数据结构：树(Tree)【详解】_数据结构 树-CSDN博客