2024小美赛
论文阅读:Jupiter: friend or foe? An answer
奥尔特云:
长周期彗星:这些天体来自奥尔特云,周期超过200年,具有完整的轨道倾角范围,由 1012-1013 个冰体组成,其中绝大多数的直径小于 10 公里,并占据一个距离太阳约 103-105 天文单位的厚球形壳
短周期彗星:一般认为来自于柯伊伯带或离散盘。周期在200年以下
短周期彗星有两大类:木星族彗星(半长轴小于5天文单位)及哈雷类彗星
木星族:木星有时会缩短一颗彗星的运动周期,有时会延长一颗彗星的运动周期,有时会改变彗星轨道,从而使得周期彗星变成非周期彗星,反过来也一样。周期3-10年,远日点在木星轨道附近的彗 星称为木星族彗星。
改变木星轨道上巨星的质量Y来 自小行星带的轰击
我们研究了改变“木星”质量对地球从小行星带向内抛出的物体所经历的撞击率的影响。我们在模拟冲击通量时遇到了一些问题。小行星被认为构成了最大的威胁。然而,在创建一群可能进化到撞击地球轨道的测试小行星时,我们面临着巨大的不确定性,特别是与整合开始时小行星的分布有关的不确定性。
因为自木星形成以来,它一直在扰乱目前在小行星带中观察到的物体的轨道。因此,尝试为这颗小行星构建一个受干扰程度要小得多的初始种群是很重要的
我们 2008 年的论文详细介绍了我们如何确定小行星分布,$\ N_{0}(a)=k(a-a_{min})^\frac{1}{2}$,其中 N(a) 是距离太阳 a 的小行星数量,k 是常数, amin 是小行星分布的内部边界。 amin的值为1.558AU,相当于火星的轨道半长轴,1.52 AU,加上三个 希尔半径
归一化常数 k 的确定 为了使总的小行星数量 Ntotal, 为一个固定值,我们需要对 N(a)进行归一化。通过对 N(a)在范 围[amin,amax]内积分,可以得到归一化常数 k
$\ k=\frac{3N_{total}}{2(a_{max}-a_{min})^\frac{2}{3}}$
希尔半径$\ R_{H}=a_p(\frac{M_{planet}}{3M_{Sun}})^\frac{1}{3}$,ap 是行星轨道的半长轴,M 表示质量。希尔球半径是一个天体对其周围物体产生重力影响的范围
以这种方式创建的物体代表一个碎片圆盘,在行星形成过程中受到了适度但不过度的搅拌(例如 Ward 2002)。
然后,在地球、火星、木星、土星、天星和海王星的影响下,使用 MERCURY 包中包含的混合积分器对测试粒子进行了 1000 万年的跟踪。进行了简单的测试积分,以检查地球横截面积对所经历的冲击通量的影响。正如预期的那样,发现撞击率与地球的横截面积成正比,引力聚焦的影响可以忽略不计。为了提高撞击率以获得合理的撞击统计数据,因此我们将地球膨胀到 106 公里的半径。在我们的整合中,小行星与行星和太阳发生引力相互作用,但彼此之间没有相互作用
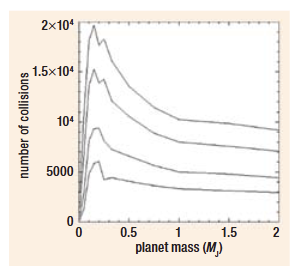
我们运行中使用的 “Jupiter” 经过修改,因此我们运行了 12 个单独的质量。在木星质量 MJ 的倍数中,这些是:0.01、0.05、0.10、0.15、0.20、0.25、0.33、0.50、0.75、1.00、1.50 和 2.00。每个“木星”的轨道元素与今天的木星相同。同样,模拟中其他行星的元素与今天相同:一次运行和下一次运行之间行星设置的唯一区别是木星质量的变化——所有其他变量都是恒定的。
显示了我们的模拟中 通量与质量关系的形式,其中小行星是 源群体。这些结果令人惊讶。在 1.00 M J 时,对地球的撞击次数约为 0.01 M J 时的撞击次数的 3.5 倍Y几乎没 有屏蔽!在这两个”木星”质量之间, 在 0.2 M J 左右存在一个峰值,其中撞 击次数几乎是 1.00 M J 时的两倍。
我们随机生成了 100 000 个测试群体粒子,近日点位于 0.1– 10 AU 范围内,远日点位于 10 000 和100 000 个AU。人口的结构是为 了模仿观察到的长周期彗星的远日点 分布。近日点距离 q 确定如下$\ q=0.1+[(q_{max}-q_{min})^\frac{2}{3}*random]^\frac{2}{3}$其中 qmax 和 qmin分别是 0.1 和 10 AU 的最大和最小可能近日点 距离,而 random 是在克隆程序中 生成的 0 到 1 之间的随机数。这导 致大约 3% 的初始样本具有与地球 轨道交叉的轨道(地球交叉轨 道),大约 38% 位于最初与木星 交叉的轨道(q 小于或等于 5.203 AU 的轨道)。这个分布是一个简 单但有效的尝试,试图拟合新奥尔 特云彗星的已知分布
我们计算了奥尔特云 彗星在(膨胀的)地球上的碰撞次 数。需要采取不同的方法。奥尔特 云彗星的轨道周期是如此之大,以 至于即使在 100 Myr 的模拟中,即 使地球严重膨胀,也很少会与地球 近距离接触。因此,为了直接确定 对地球的撞击率,我们必须模拟大 量的测试粒子,其数量级比所使用 的粒子高出许多数量级
我们模拟中使用的”木 星”的质量被修改了从一个场景到 下一个场景。总共考虑了五种不同 的场景。研究了质量为木星质量 0.25、0.50、1.00 和 2.00 倍 的”木星”系统,以及不存在木星 的系统。和以前一样,场景之间的 唯一区别是木星的质量Y所有其 他参数都是恒定的。
大质量情况下彗星的消失速度 明显快于低质量木星的情况。即使 仅在 1 Myr 后,木星质量较高的喷 射率就很明显,并且一直持续到我 们模拟的最后,到那时,在所有情 况下,仅保留了初始彗星种群的一 小部分。
值得注意的是,即使没有 木星存在,到运行结束时,长周期 彗星的数量仍然会显着减少。由于 木星不存在(“木星”质量为 零)
。当考虑基于喷射率的初始代理 的结果时,重要的是要确保该措施 是实际上是冲击通量的合适代理。 例如,地球上的碰撞率似乎可能并 不简单地与幸存的奥尔特云彗星的 数量成正比。特别是,另外两种可 能性似乎值得进一步研究,以确保 我们最初的假设是正确的:考虑到 所研究的彗星轨道的扩展,重要的 是要检查是否存在穿过地球轨道的 奥尔特云彗星的优先生存( q < 1 AU),或那些不存在的 (q > 1 AU)。
换句话说,当考虑到长周期彗星通量(与我们之前 的发现相反),一颗质量更大的木星 肯定会在不存在这样的行星的情况下 为地球提供一些可测量的屏蔽。
事实上,只有在来自奥尔特 云的彗星的情况下,我们的结果表 明木星确实是长期以来所假设的地 球的朋友!
然而,应该指出的 是,在长周期轨道上运动的物体平 均而言通常比在短周期或星状轨道 上运动的物体具有更大的碰撞速度 (这是由于它们较高的倾角[包括逆 行轨道]和更大的轨道)速度为 1 天 文单位),这增加了奥尔特云彗星 作为轰炸机群体的相对重要性。
作 为一个整体,我们的工作表明,而 不是充当作为地球的盾牌,木星反 而增加了我们星球所经历的冲击通 量,超过了如果这颗行星以某种方 式神奇地从我们的太阳系中移走时 所受到的冲击通量。然而,如果木 星的质量减少到土星的质量,地球 的情况会更糟
事实上,只有在来自奥尔特 云的彗星的情况下,我们的结果表 明木星确实是长期以来所假设的地 球的朋友!
我们的结果令人震惊。对于当前时代威胁地球的两个主要种群(近地小行星 和短周期彗星),我们发现木星质量与撞击率之间的关系相当复杂。在”木星”质量 较低的情况下,两颗行星的撞击率都非常低,因为这些小行星很难在地球交叉轨道上 放置物体。同样,在高”木星”质量(类似于或大于我们的木星)时,两个种群的撞 击率都相对较低,尽管略高于质量最小的”木星”。然而,在这两个极端之间,我们 在模拟中发现地球上的撞击通量出现了显着的峰值。对于近地小行星(Horner & Jones, ̚ ̘ ̘ ̠ b)和短周期彗星(Horner & Jones, 2009),我们发现当模拟中的”木 星”在0.2到0.3倍之间时,撞击通量最大。和我们的木星一样大。换句话说,与质量 小得多的情况相比(例如,当它的质量与海王星相当时),我们的木星仅提供适度的 屏蔽,但如果它围绕土星的质量,那么地球上的撞击通量将是远远大于我们观察到 的。
当我们研究木星质量对第三种潜在危险天体M长周期彗星M的撞击率的影响时 (例如 Wiegert & Tremaine, 1999, Levison, Dones &Duncan, 2001, Horner & Evans, 2002),我们发现”木星”质量越大,对地球的撞击率就越低(Horner,Jones &钱伯斯, 2010)。那么,对于长周期彗星来说,木星似乎确实起到了盾牌的作用。然而,长周期彗星 被认为只对小行星和彗星对地球的影响贡献了一小部分(
这是否也在确定其宿主系统中潜在宜居行星的撞击通量中 发挥作用?在这项工作中,我们通过检查木星轨道偏心率和倾角的影响,建立在早期结果 的基础上。在这项工作中,我们只考虑两个主要的撞击星群M近地小行星和短周期彗星。 由于长周期彗星在轨道倾角基本上各向同性分布的轨道上运行,并且几乎不受太阳系引力 约束,因此可以合理地假设木星轨道的微小变化对彗星通量几乎没有影响或没有影响。
总体而言,很明显,巨行星轨道偏心率的增加会导致近地小行星和短周期彗星对地球的 撞击通量增加。