图的基本概念和术语
定义:一个图可以利用两个集合进行定义。第一个集合是点的集合,这些点在图术语中一般被称(Vertex);第二个集合是连接两个顶点的边(Edge)的集合。图的具体定义如下。
图是由顶点集合及顶点间的关系集合组成的一种数据结构:Graph = (V, E)
基本术语
有向图
无向图
邻接点
顶点的度,入度与出度
权和网:
权 :
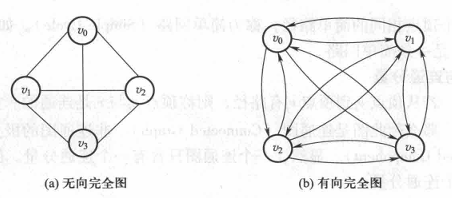
某些图的每条边都可能赋予一个数值,这个数值称为权。网 : 带有权的图称为网。 无向完全图:
任意两个顶点之间都有一条边的无向图。
有向完全图:
任意两个顶点之间都有方向相反的两条边的有向图。
image-20241202190122603
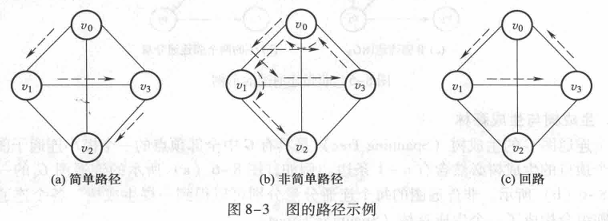
路径与路径长度
简单路径 :若路径上经过的各顶点均不重复,则称这样的路径为简单路径。
回路或环 :若路径上的第一个顶点与最后一个顶点相同,则称这样的路径为回路或环。
image-20241202190704319
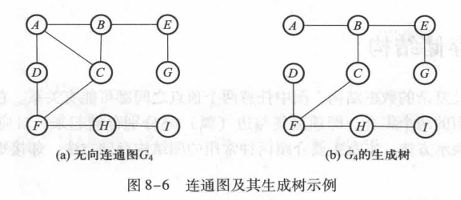
连通图:
在无向图中,若任意两个顶点之间都存在路径,则称该图为连通图。
连通分量:
非连通图的极大连通子图称为连通分量。也就是说,一个连通分量是一个连通的子图,且不能再扩大。
强连通图: 在有向图中,若对于任意一对顶点 u 和
v,都存在一条从 u 到 v 和从 v 到 u 的路径,则称该图为强连通图。
强连通分量:
非强连通图的极大强连通子图称为强连通分量。
生成树:
一个连通图的生成树是包含图中所有顶点的极小连通子图。也就是说,生成树是一棵树,且包含图中的所有顶点。
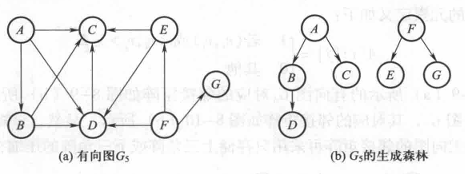
生成森林:
非连通图的每个连通分量分别可以得到一棵生成树,这些生成树的集合称为生成森林。
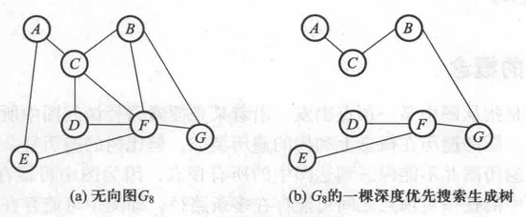
image-20241202191533963
image-20241202191543162
图的储存结构
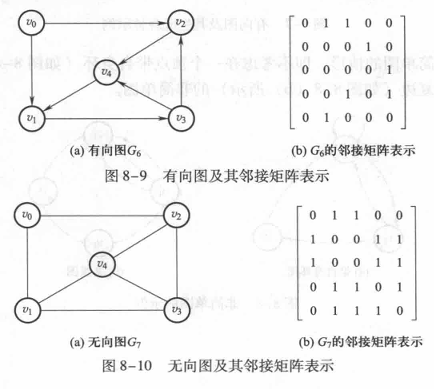
邻接矩阵
邻接矩阵表示法的基本思想是引入两个数组:
一个用于记录图中各个顶点信息的—维数组,称为顶点表;
另一个用于表示图中各个顶点之间关系的二维数组,称为邻接矩阵。
设图G=(V,
E)是具有n(n>0)个顶点的图,则图G所对应的邻接矩阵A是一个n阶方阵
image-20241202192441396
image-20241202192456777
无向图的邻接矩阵可采用只存储上三角阵或下三角阵的压缩存储方法
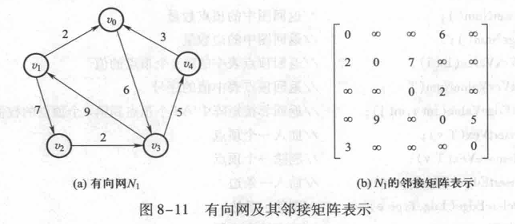
对于带权图,需要对邻接矩阵的元素值定义进行修改,让元素值表示相应顶点的权值
image-20241202192636345
其中,∞可用计算机中的一个足够大的数代替,以与权重区分
image-20241202193146935
算法
图类MGraph的定义
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 enum GraphType { undigraph, digraph, undinetwork, dinetwork };template <class T >struct EdgeType { T head, tail; int cost; EdgeType (T h, T t, int c) { head = h; tail = t; cost = c; } }; template <class T >class MGraph {private : int vexnum, edgenum; GraphType kind; vector<vector<int >> edges; vector<T> vexs; };
无向有权图的邻接矩阵构建
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 void createAdjMatrix (vector<vector<int >>& adjMatrix, const vector<tuple<int , int , int >>& edges, int numVertices) for (int i = 0 ; i < numVertices; ++i) { for (int j = 0 ; j < numVertices; ++j) { if (i != j) adjMatrix[i][j] = INT_MAX; } } for (const auto & edge : edges) { int u = get <0 >(edge); int v = get <1 >(edge); int weight = get <2 >(edge); adjMatrix[u][v] = weight; adjMatrix[v][u] = weight; } }
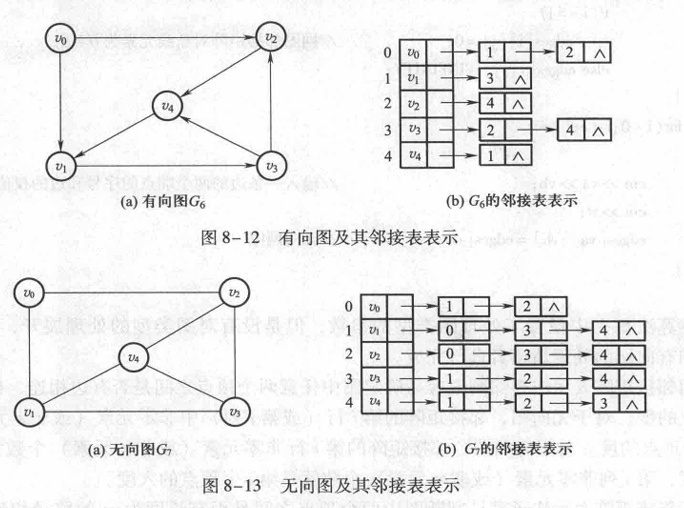
邻接表
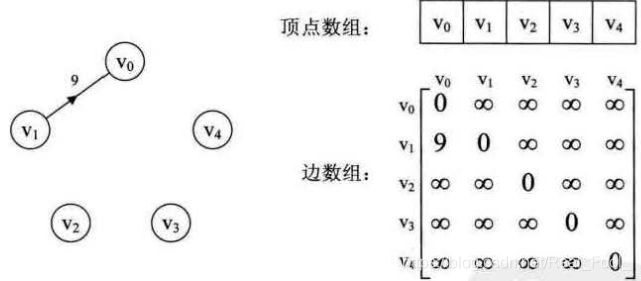
当一个图为稀疏图时(边数相对顶点较少),使用邻接矩阵法显然要浪费大量的存储空间,如下图所示:
dc28a71607451fd5adeb57fadf14659b
邻接表中存在两种结点:顶点表结点和边表结点,如下图所示。
5257342f8b24df2a6af18a35e74af60b
顶点表结点由顶点域(data)和指向第一条邻接边的指针(firstarc)
构成,边表(邻接表)结点由邻接点域(adjvex)和指向下一条邻接边的指针域(nextarc)
构成。
image-20241205203225293
算法
基于邻接表存储表示的图类ALGraph定义
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 struct EdgeNode { int adjvex; EdgeNode* next; }; template <class T >struct VexNode { T data; EdgeNode* firstEdge; }; template <class T >class ALGraph { vector<VexNode<T>> vex; int vexnum, edgenum; GraphType kind; };
无向图的构建
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 template <class T >ALGraph<T>::ALGraph (GraphType t, T vexs[], int n, int e) { vexnum = n; edgenum = e; kind = t; adjlist.resize (vexnum); for (int i = 0 ; i < vexnum; ++i) { adjlist[i].data = vexs[i]; adjlist[i].firstEdge = 0 ; } for (int j = 0 ; j < edgenum; j++) { int va, vb; cin >> va >> vb; EdgeNode* p = new EdgeNode; p->adjvex = vb; p->nextedge = adjlist[va].firstEdge; adjlist[va].firstEdge = p; p = new EdgeNode; p->adjvex = va; p->nextedge = adjlist[vb].firstEdge; adjlist[vb].firstEdge = p; } }
图的遍历
为了防止已经访问过的结点重复访问的问题,提出了辅助数组
visited[]
深度优先遍历
深度优先搜索类似于树的先序遍历。
image-20241205210048064
算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 bool visited[MAX_VERTEX_NUM]; void DFS (Graph G, int v) int w; visit (v); visited[v] = TRUE; for (w = FirstNeighbor (G, v); w>=0 ; w=NextNeighor (G, v, w)){ if (!visited[w]){ DFS (G, w); } } } void DFSTraverse (MGraph G) int v; for (v=0 ; v<G.vexnum; ++v){ visited[v] = FALSE; } for (v=0 ; v<G.vexnum; ++v){ if (!visited[v]){ DFS (G, v); } } }
DFS算法是一个递归算法,需要借助一个递归工作栈,故其空间复杂度为O(V)。
对于n个顶点e条边的图来说,邻接矩阵由于是二维数组,要查找每个顶点的邻接点需要访问矩阵中的所有元素,因此都需要O(V^2)的时间。而邻接表做存储结构时,找邻接点所需的时间取决于顶点和边的数量,所以是O(V+E)。
广度优先遍历
图的广度优先遍历就类似于树的层序遍历
算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 void BFSTraverse (MGraph G) int i, j; Queue Q; for (i = 0 ; i<G,numVertexes; i++){ visited[i] = FALSE; } InitQueue (&Q); for (i=0 ; i<G.numVertexes; i++){ if (!visited[i]){ vivited[i] = TRUE; visit (i); EnQueue (&Q, i); while (!QueueEmpty (Q)){ DeQueue (&Q, &i); for (j=FirstNeighbor (G, i); j>=0 ; j=NextNeighbor (G, i, j)){ if (!visited[j]){ visit (j); visited[j] = TRUE; EnQueue (Q, j); } } } } } }
无论是邻接表还是邻接矩阵的存储方式,BFS算法都需要借助一个辅助队列Q,
n个顶点均需入队一次,在最坏的情况下,空间复杂度为O(V)。
采用邻接表存储方式时,每个顶点均需搜索一次(或入队一次),在搜索任一顶点的邻接点时,每条边至少访问一次,算法总的时间复杂度为O(V+E)。采用邻接矩阵存储方式时,查找每个顶点的邻接点所需的时间为O(V),故算法总的时间复杂度为O(V^2)。
注意:图的邻接矩阵表示是唯一的,但对于邻接表来说,若边的输入次序不同,生成的邻接表也不同。因此,对于同样一个图,基于邻接矩阵的遍历所得到的DFS序列和BFS序列是唯一的,基于邻接表的遍历所得到的DFS序列和BFS序列是不唯一的。
应用
简单路径的搜索算法 dfs
二部图的判定算法
最小生成树
生成树变成非连通图;若给它增加一条边,则会形成图中的一条回路。对于一个带权连通无向图G=(V,E),生成树不同,其中边的权值之和最小的那棵生成树(构造连通网的最小代价生成树),称为G的最小生成树(Minimum-Spanning-Tree,MST) 。
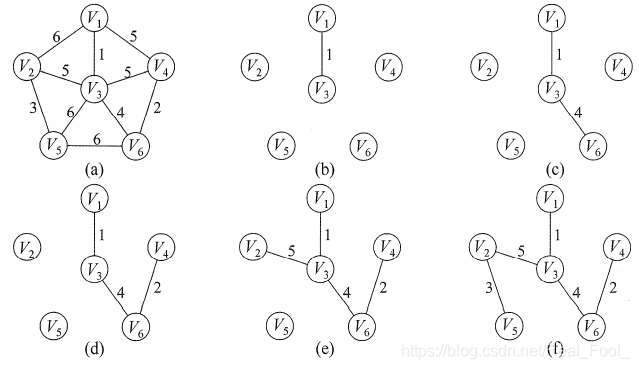
普里姆(Prim)算法
从一个顶点出发,在保证不形成回路的前提下,每找到并添加一条最短的边,就把当前形成的连通分量当做一个整体或者一个点看待,然后重复“找最短的边并添加”的操作。
d0daac1cd8df11a443697ee6bc3fcf03
引入辅助数组miniedges[],用于存放每个节点到节点v的边的权值,并每次挑选出权值最小的那个边所对应的节点加入生成树,辅助数组miniedges[]的数据类型如下
1 2 3 4 struct Edge { int adjvex; int lowcost; };
若将某个数组元素miniedges[i]的
lowcost成员值设为0,则表示相应的顶点v,已加入到最小生成树中。
为便于算法在执行过程中读取任意两个顶点之间边的权值,对图宜采用邻接矩阵存储结构 。
算法思路:
初始化辅助数组,从节点v开始,将v的lowcost设为0,说明已经加入生成树
循环vexnum-1次,利用函数MiniNum找到权值最小的节点并输出
函数MiniNum循环vexnum次,找到当前所有节点中,未加入生成树的 ,lowcost最小的节点
更新辅助数组miniedges[]的每个节点的lowcost:循环vexnum次,如果通过当前节点k能找到比原先更小的边,更新该节点的lowcost;如果大,则保留原lowcost的值,更新后代表生成树节点的集合到未加入节点的集合的权值最小的vexnum条边
时间复杂度:O(n^2)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 void Prim (const vector<vector<int >>& graph, int v, int vexnum) Edge* miniedges = new Edge[vexnum]; for (int i = 0 ; i < vexnum; i++) { miniedges[i].adjvex = GetVexValue (v); miniedges[i].lowcost = GetEdgeValue (graph, v, i); } miniedges[v].lowcost = 0 ; for (int i = 1 ; i < vexnum; i++) { int k = MiniNum (miniedges, vexnum); cout << miniedges[k].adjvex << " --> " << GetVexValue (k) << endl; miniedges[k].lowcost = 0 ; for (int j = 0 ; j < vexnum; j++) { if (GetEdgeValue (graph, k, j) < miniedges[j].lowcost) { miniedges[j].adjvex = GetVexValue (k); miniedges[j].lowcost = GetEdgeValue (graph, k, j); } } } delete [] miniedges; }
函数MiniNum用于在数组miniedges中查找集合V-U中的具有最小权值的顶点,可以将它定义为私有成员函数
1 2 3 4 5 6 7 8 9 10 11 12 int MiniNum (Edge miniedges[], int vexnum) int min = INT_MAX; int k = -1 ; for (int i = 0 ; i < vexnum; i++) { if (miniedges[i].lowcost != 0 && miniedges[i].lowcost < min) { min = miniedges[i].lowcost; k = i; } } return k; }
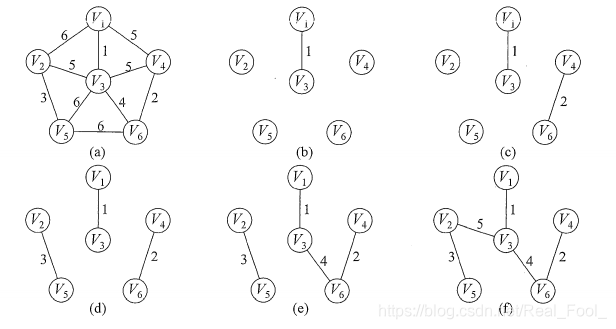
克鲁斯卡尔(Kruskal)算法
与Prim算法从顶点开始扩展最小生成树不同,Kruskal
算法是一种按权值的递增次序选择合适的边来构造最小生成树的方法。
每次挑选为加入生成树的最小边,若不构成回路,则加入生成树,若构成则挑选下一个
6b95ef2bc34f407c122e931cf06b11e6
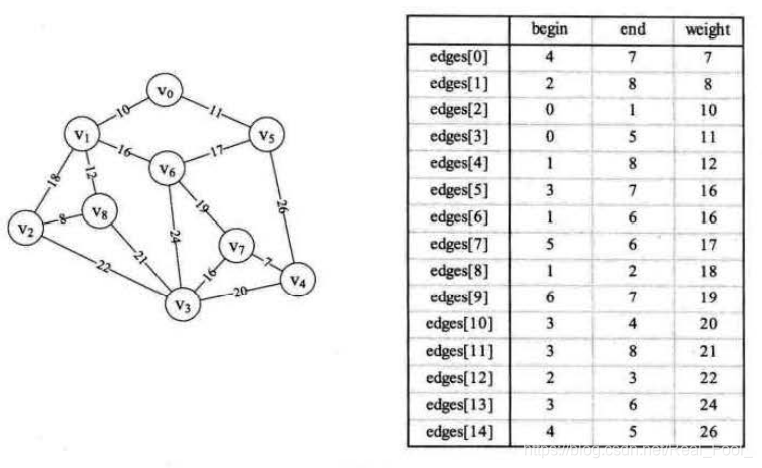
为提高算法执行过程中查找最小权值边的速度 ,可以采用一种排序算法(如堆排序算法)对边集数组中的边按权值进行排序。
接下来,Kruskal算法的关键问题就是如何判断所选取的边加入T中是否会产生回路 ,这里通过引入称为并查集 的数据结构来解决
fb9515df040633c09b3c136601c8dbd7
在下面描述的Kruskal 算法实现中,首先利用私有成员
GetGraph()函数将图的边按权值排好序后存入边集数组graph中 ,而边集数组tree则用于保存和返回算法所构造的最小生成树T 。
算法思路:
初始话数组graph,用于存放所有的边,并对其排序
并查集的使用利用数组components,先进行初始化,每个节点的祖先都是自己,也可以理解成每个节点都构成一个集合,后续并查集的过程即为集合合并的过程
循环直到找到最小生成树的所有边(vexnum -
1条),对于每条边,查找他的起点和终点节点的祖先,若是一个祖先则说明在同一集合,不能加入到生成树;若不是一个,则可以加入到生成树数组tree,并要修改节点的祖先,使他们集合合并
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 template <class T >void MGraph<T>::Kruskal (vector<EdgeType> &tree) { vector<EdgeType> graph; GetGraph (graph); tree.resize (vexnum - 1 ); int *components = new int [vexnum]; for (int i = 0 ; i < vexnum; i++) { components[i] = i; } int k = 0 , j = 0 ; while (k < vexnum - 1 ) { int h1 = graph[j].head; int t1 = graph[j].tail; int h2 = components[h1]; int t2 = components[t1]; if (h2 != t2) { tree[k].head = h1; tree[k].tail = t1; tree[k].cost = graph[j].cost; k++; for (int i = 0 ; i < vexnum; i++) { if (components[i] == t2) { components[i] = h2; } } } j++; } delete [] components; }
显然,Kruskal算法的效率与所选择的排序算法的效率 以及并查集数据结构的实现效率 有关。若采用第10章介绍的比较高效的堆排序算法 排序,并查集采用树结构 实现,则Kruskal算法的时间复杂度可达到O( e l o g 2 e )。相比
Prim
算法而言,Kruskal算法更适用于求解稀疏网(指边数较少的网)的最小生成树。
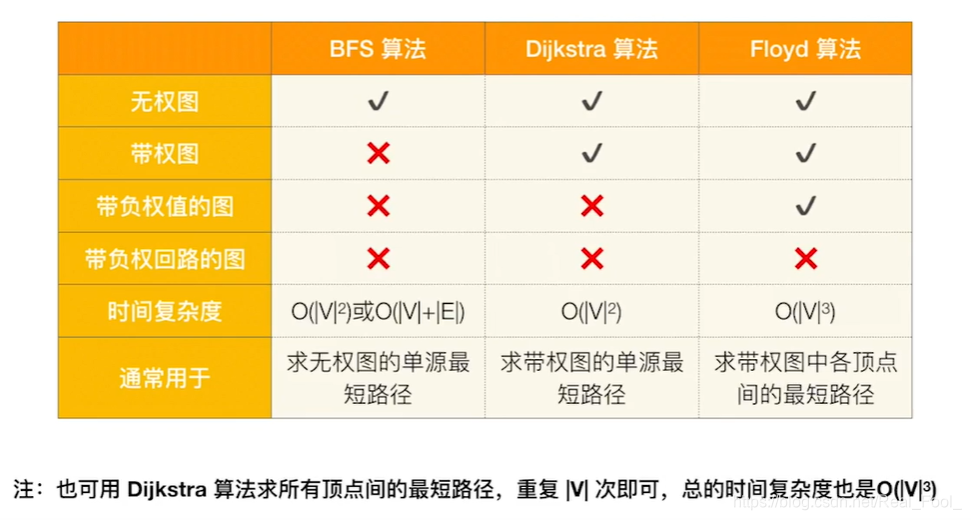
最短路径
在网图和非网图中,最短路径的含义是不同的。由于非网图它没有边上的权值,所谓的最短路径,其实就是指两顶点之间经过的边数最少的路径;而对于网图来说,最短路径,是指两顶点之间经过的边上权值之和最少的路径,并且我们称路径上的第一个顶点是源点,最后一个顶点是终点。
求图的最短路径问题通常可分为两类。一类是求图中某顶点到其余各顶点的最短路径问题,也称为单源最短路径问题 ;另一类是求图中每对顶点之间的最短路径问题。
迪杰斯特拉( Dijkstra )算法
Dijkstra算法用于构建单源点的最短路径—,即图中某个点到任何其他点的距离都是最短的。例如,构建地图应用时查找自己的坐标离某个地标的最短距离。可以用于有向图,但是不能存在负权值。
通俗点说,迪杰斯特拉(Dijkstra)算法,它并不是一下子求出了 v i 到 v j 的最短路径,而是一步步求出它们之间顶点的最短路径,过程中都是基于已经求出的最短路径的基础上,求得更远顶点的最短路径,最终得到你要的结果。
下面介绍
Dijkstra算法的具体实现。为便于在算法执行过程中快速地求得任意两个顶点之间边的权值,图的存储结构宜采用邻接矩阵方式。
为标识图中各顶点在算法执行过程中是否已求出最短路径 ,设置一个一维数组s[]
为记录
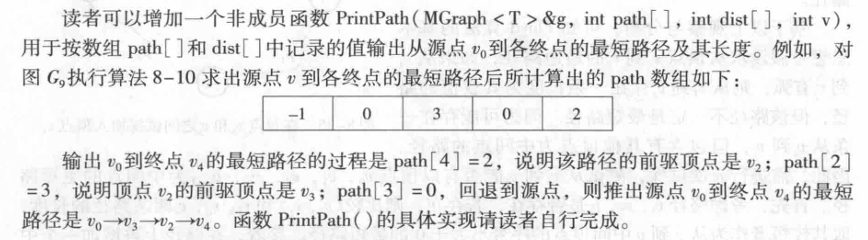
Dijkstra算法所求出的从源点到各顶点的最短路径,引入数组 path[],
path[i]中保存了从源点到终点v,的最短路径上该顶点的前驱顶点的序号 。算法结束时,可根据数组path[
]找到源点到v,的最短路径上每个顶点的前驱顶点,并一直回溯至源点,从而推出从源点到v的最短路径。
为便于每次从V-S中选择当前离源点距离最短的顶点,需要引人一个辅助数组dist[]。它的每一个分量dist[i]表示当前所确定的从源点 v 0 ,到终点 v i 的最短路径.
算法思路:
初始化,s[]所有值为0,s[0]设置为1,代表从 v 0 节点开始,path[]所有值设为0,path[0]设为-1,dist[]通过查找邻接矩阵,得到 v 0 到各个顶点的值
查找dist中最小的值,从该节点继续完成最小路径,将该节点对应s[]设为1
遍历尚未找到最短路径的节点,即s[]为0,dist[i] = Min{dist[i],dist[j]
+cost(j,i)},选择是借用上一个最短路径的节点到达还是直接到达,更新dist的值
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 void dijkstra (int start, int dist[], int path[]) int n = numVertices; bool visited[n]; for (int i = 0 ; i < n; ++i) { visited[i] = false ; dist[i] = adjMatrix[start][i]; if (dist[i] != INT_MAX || i == start) { path[i] = start; } else { path[i] = -1 ; } } dist[start] = 0 ; visited[start] = true ; for (int count = 0 ; count < n - 1 ; ++count) { int min = INT_MAX, min_index; for (int v = 0 ; v < n; ++v) { if (visited[v] == false && dist[v] <= min) { min = dist[v]; min_index = v; } } visited[min_index] = true ; for (int v = 0 ; v < n; ++v) { if (!visited[v] && dist[v] > dist[min_index] + adjMatrix[min_index][v]) { dist[v] = dist[min_index] + adjMatrix[min_index][v]; path[v] = min_index; } } } }
image-20241209092422699
1 2 3 4 5 6 7 8 9 10 11 12 13 14 void PrintPath (const vector<vector<int >>& g, vector<int > path, vector<int > dist, int v) if (dist[v] == INF) { cout << "节点 " << v << " 无法到达" << endl; return ; } if (path[v] != -1 ) { PrintPath (g, path, dist, path[v]); } cout << v << " " ; }
时间复杂度O(n^2)
弗洛伊德( Floyd )算法
e00a2f6ecb05b16c2cae4adfb9da8698
算法原理:递归
n阶数组D:用于保留每一步所求得的所有顶点对之间的当前最短路径长度
初始化: D [i ][j ] = c o s t (i , j ) 用邻接矩阵进行初始化
状态转移方程: D k i ][j ] = m i n {D k − 1i ][j ], D k − 1i ][k ] + D k − 1k ][j ]} 更新v i v j
path数组:用于存储最短路径,初始化若没有直接路径则 p a t h [i ][j ] = −1 ,若有则 p a t h [i ][j ] = j
算法思路:
初始化数组,遍历n*n次,即v i v j v j v i
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 template <class T >void MGraph<T>::Floyd (int path[][MAXV], int D[][MAXV]) { for (int i = 0 ; i < vexnum; ++i) { for (int j = 0 ; j < vexnum; ++j) { D[i][j] = edges[i][j]; if (D[i][j] < INF && i != j) path[i][j] = j; else path[i][j] = -1 ; } } for (int k = 0 ; k < vexnum; ++k) { for (int i = 0 ; i < vexnum; ++i) { for (int j = 0 ; j < vexnum; ++j) { if (D[i][k] != INF && D[k][j] != INF && D[i][k] + D[k][j] < D[i][j]) { D[i][j] = D[i][k] + D[k][j]; path[i][j] = path[i][k]; } } } } }
函数OutputPath用于输出保存于二维数组path中的所有路径以及保存于二维数组D中的路径长度
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 template <class T >void OutputPath (MGraph<T> &G, int path[][MAXV], int D[][MAXV]) for (int i = 0 ; i < G.vexnum; ++i) { for (int j = 0 ; j < G.vexnum; ++j) { if (i != j) { if (D[i][j] == INF) { std::cout << "Path from " << i << " to " << j << ": No path exists.\n" ; } else { std::cout << "Path from " << i << " to " << j << " (Length: " << D[i][j] << "): " ; int temp = i; std::cout << temp; while (temp != j) { temp = path[temp][j]; std::cout << " -> " << temp; } std::cout << std::endl; } } } } }
AOV网与拓扑排序
有向无环图:不含环的有向图
AOV网 :在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系,这样的有向图为顶点表示活动的网
拓扑序列 :设G=(V,E)是一个具有n个顶点的有向图,V中的顶点序列V,
V2 ,..V
n,满足若从顶点V到V;有一条路径,则在顶点序列中顶点V必在顶点V;之前。则我们称这样的顶点序列为一个拓扑序列。
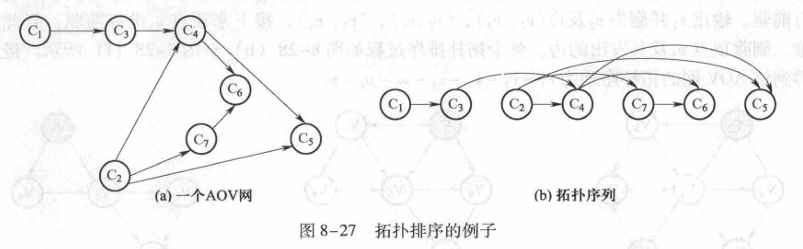
拓扑排序 :其实就是对一个有向图构造拓扑序列的过程 。每个AOV网都有一个或多个拓扑排序序列。
image-20241215131046998
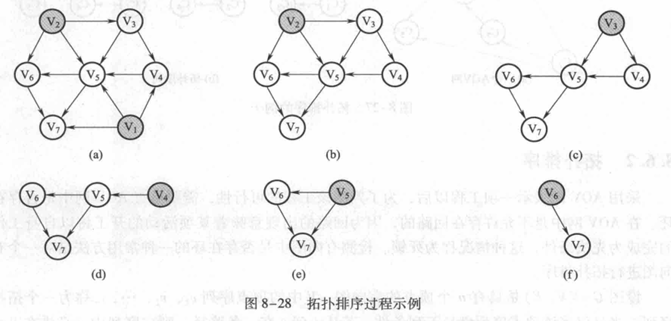
对一个AOV网进行拓扑排序的算法有很多,下面介绍比较常用的一种方法的步骤:
①从AOV网中选择一个没有前驱的顶点并输出。
②从网中删除该顶点和所有以它为起点的有向边。
③重复①和②直到当前的AOV网为空或当前网中不存在无前驱的顶点为止。如果输出顶点数少了,哪怕是少了一个,也说明这个网存在环(回路),不是AOV网。
算法原理:dfs
对于AOV 网宜采用邻接表 作为存储结构
数组indegree:用于存放各个顶点的入度
算法思路:
每次遍历数组indegree,查找入度为零的顶点,将其加入队列,再遍历邻接表,将遍历到的顶点的indegree值减一,并判断是否为零,若为零则加入队列
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 void Graph::topologicalSort () vector<int > indegree (V, 0 ) ; queue<int > q; for (int i = 0 ; i < V; i++) { for (int v : adj[i]) { indegree[v]++; } } for (int i = 0 ; i < V; i++) { if (indegree[i] == 0 ) { q.push (i); } } int count = 0 ; cout << "拓扑排序顺序为: " ; while (!q.empty ()) { int u = q.front (); q.pop (); cout << u << " " ; count++; for (int v : adj[u]) { indegree[v]--; if (indegree[v] == 0 ) { q.push (v); } } } cout << endl; if (count != V) { cout << "图中存在环,无法进行拓扑排序!" << endl; } }
参考文献
数据结构:图(Graph)【详解】_图数据结构-CSDN博客
数据结构-图-prim(普里姆)算法最小生成树(过程分析+手写代码)_哔哩哔哩_bilibili
数据结构-图-最小生成树-克鲁斯卡尔(Kruskal)算法-手画+过程分析+代码_哔哩哔哩_bilibili