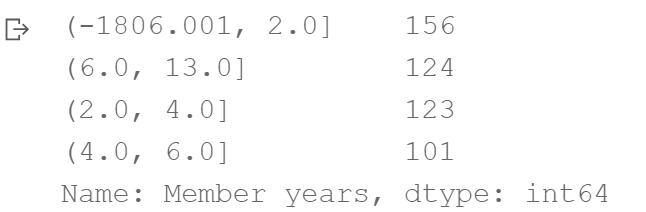机器学习——第二次上机——数据预处理基础

发表于 更新于 分类于 ， 阅读次数：

机器学习数据预处理基础

1. One-Hot编码

任务介绍

  • 使用Pandas中的value_counts()函数，查看data中的特征User continent的取值类型， 并打印输出的内容；
  • 使用pandas中的getdummies()函数对data中的特征User continent进行One-Hot编码，参数prefix为User continent；
  • 将编码后的结果保存在encode_uc中，并输出变量的前5行内容。

预期实验结果


补全代码;

1
2
3
4
5
6
7
8
9
10
import pandas as pd 
data = pd.read_csv('user_review.csv')
# 请在下方作答 #
# value_counts() 函数统计并输出 "User continent" 列中各大陆出现的次数
print(data['User continent'].value_counts())
# 使用 get_dummies() 对 "User continent" 列进行 One-Hot 编码
# One-hot编码是一种将类别变量转换为多个二进制特征列的技术，
# 每个类别对应一列，如果该行数据属于该类别则取值为1，否则为0
encode_uc = pd.get_dummies(data['User continent'], prefix='User continent_')
print(encode_uc)

​ User continent
​ North America 296
​ Europe 118
​ Oceania 41
​ Asia 36
​ Africa 7
​ South America 6
​ Name: count, dtype: int64
​ User continentAfrica User continentAsia User continentEurope \
​ 0 False False False
​ 1 False False False
​ 2 False False False
​ 3 False False True
​ 4 False False False
​ .. … … …
​ 499 False False True
​ 500 False False False
​ 501 False False False
​ 502 False False False
​ 503 False False False
​
​ User continentNorth America User continentOceania \
​ 0 True False
​ 1 True False
​ 2 True False
​ 3 False False
​ 4 True False
​ .. … …
​ 499 False False
​ 500 True False
​ 501 True False
​ 502 True False
​ 503 True False
​
​ User continentSouth America
​ 0 False
​ 1 False
​ 2 False
​ 3 False
​ 4 False
​ .. …
​ 499 False
​ 500 False
​ 501 False
​ 502 False
​ 503 False
​
​ [504 rows x 6 columns]
​

2. 缺失值填补

任务介绍

  • 使用pandas中的value_counts()函数打印输出data中的特征Traveler type的取值统计信息， 并查看其是否含有缺失值；
  • 如果存在缺失值，将特征Traveler type在其他样本中取值频数最多的值保存在变量freq_v中，并使用freq_v进行缺失值填充；
  • 再次打印输出特征Traveler type的取值统计信息。

预期实验结果

补全代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import pandas as pd 
data = pd.read_csv('user_review.csv') 

# value_counts(dropna=False) 会包括缺失值（NaN）在内
print(data['Traveler type'].value_counts(dropna=False))


# idxmax()会获取频数最多的取值
freq_v = data['Traveler type'].value_counts().idxmax()

# freq_v会替代缺失值
data['Traveler type'] = data['Traveler type'].fillna(freq_v)

### 打印
print('')
print(u'缺失值填充完之后：')
print( '')
print(data['Traveler type'].value_counts(dropna=False))

3. 特征标准化

任务1:

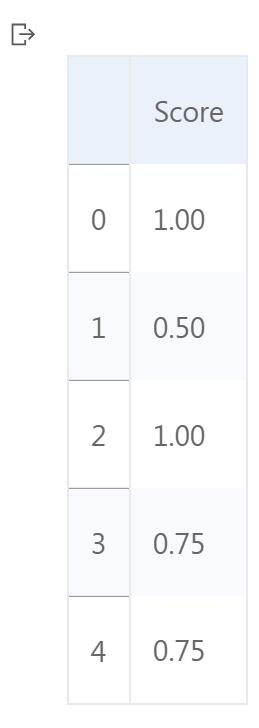
  • 使用sklearn中preprocessing模块下的StandardScaler()函数对data的特征Score进行Z-score标准化；
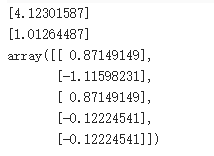
  • 将特征取值的均值保存在变量score_mean中，并打印；
  • 将特征取值的方差保存在变量score_var中，并打印。

预期实验结果

fa64d89b-3dc9-4b07-b27f-210b56e583ed

补全代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import pandas as pd 
# sklearn是一个用于机器学习的Python库，提供了各种分类、回归、聚类算法，
# 包括支持向量机、随机森林、梯度提升等。它还包含了用于数据预处理、特征提取和模型选择的工具。
from sklearn.preprocessing import StandardScaler
data = pd.read_csv('user_review.csv')

# 请在下方作答 #
## 创建Z-score对象
## Z-score标准化是一种将数据转换为均值为0，标准差为1的标准正态分布的方法

## 初始化StandardScaler对象，用于执行Z-score标准化
std_scaler = StandardScaler()

## Score特征标准化，使用fit_transform()方法
# fit_transform() 会先计算出该特征的均值和标准差，然后进行标准化
normal_df = std_scaler.fit_transform(data[['Score']])  

## 均值
# StandardScaler 会自动计算并存储 'Score' 列的均值，这个值在标准化过程中用来进行数据转换
score_mean = std_scaler.mean_

## 方差
# 方差也是 StandardScaler 会计算的一个参数，表示数据的离散程度
score_var = std_scaler.var_

## 打印
print (score_mean)
print (score_var)

## 打印前五行内容
normal_df[:5]

​ [4.12301587]
​ [1.01264487]
​

​ array([[ 0.87149149],
​ [-1.11598231],
​ [ 0.87149149],
​ [-0.12224541],
​ [-0.12224541]])

任务2：

  • 自定义函数min_max()实现MinMax标准化，输入参数data为要进行标准化的数据，输出为标准化后的数据。
  • 使自定义的min_max()函数对data的特征Score进行MinMax标准化，输出结果保存在score_transformed中，并打印变量的前5行内容

预期结果

补全代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import pandas as pd 
data = pd.read_csv('user_review.csv')

# 请在下方作答 #
def min_max(data):
    
    ## 最小值
    data_min = data.min()
    ## 最大值
    data_max = data.max()
    ## 最大值与最小值之间的差值
    data_range=data_max-data_min
    ## 根据MinMax标准化的定义实现
    #MinMax 标准化（最小-最大标准化）是一种数据预处理方法，
    # 旨在将数据的所有特征（列）缩放到一个指定的范围，通常是 [0, 1]。
    # 这种标准化方法将原始数据通过线性变换映射到新的范围。
    new_data = (data-data_min)/data_range# MinMax标准化公式： (x - min) / (max - min)
    
    ## 返回结果
    return new_data

## 调用min_max()函数
score_transformed = min_max(data['Score'])

## 打印变量的前5行内容
score_transformed.head()

​ 0 1.00
​ 1 0.50
​ 2 1.00
​ 3 0.75
​ 4 0.75
​ Name: Score, dtype: float64

任务3：

  • 自定义logistic()函数，输入参数为要进行标准化的数据，输出结果为经过标准化后的数据；
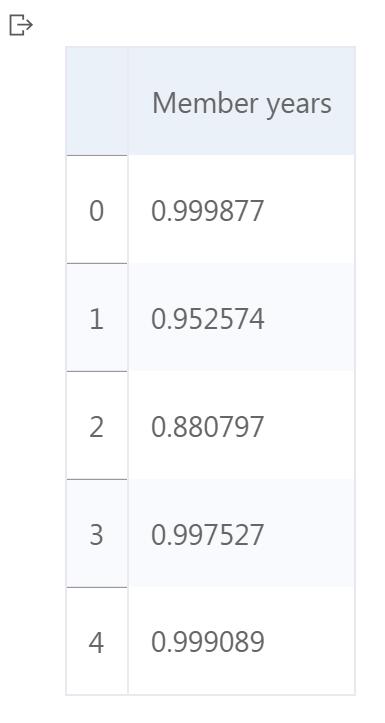
  • 使用自定义函数对data的特征Member years进行Logsitic标准化，结果保存在member_transformed中，并输出变量的前5行内容。

预期结果：

补全代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#ogistic 标准化（Logistic Normalization）是一个将数据转换为 (0, 1) 范围的过程，
# 通常使用 Logistic 函数（也称为 Sigmoid 函数）。
# 它是一种非线性转换方法，常用于神经网络和其他需要将数据映射到概率范围的场景。
import pandas as pd 
data = pd.read_csv('user_review.csv')

# 请在下方作答 #
def logistic(data):
    
    import numpy as np
    import warnings
    warnings.filterwarnings("ignore")
    
    ## 计算 1 + e^(-x)
    denominator = 1+ np.exp(-data)# 使用 np.exp() 计算 e^(-x)
    
    ## 实现logistic标准化
    new_data = 1/denominator
    ## 返回结果
    return new_data

## 对特征Member years进行logsitic标准化
member_transformed = logistic(data['Member years']) 

## 打印内容
member_transformed.head()

​ 0 0.999877
​ 1 0.952574
​ 2 0.880797
​ 3 0.997527
​ 4 0.999089
​ Name: Member years, dtype: float64

4. 特征离散化

任务介绍

  • 使用Pandas的qcut()函数对data中的特征Member years进行等频离散化，结果保存在bins中；
  • 使用pd.value_counts()函数统计categorical对象bins的取值信息。

预期结果

补全代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import pandas as pd 
data = pd.read_csv('user_review.csv')

# 请在下方作答 #

## 返回bins
# q=4 表示将数据分成 4 个区间
bins = pd.qcut(data['Member years'], q=4, labels=["(-1806.001, 2.0]", "(2.0, 4.0]", "(4.0, 6.0]", "(6.0, 13.0]"])

## 统计取值信息
# 使用value_counts()函数统计bins中每个类别的数量，得到离散化后的各个类别的分布情况
value_counts = pd.value_counts(bins)  

print(value_counts)

​ Member years
​ (-1806.001, 2.0] 156
​ (6.0, 13.0] 124
​ (2.0, 4.0] 123
​ (4.0, 6.0] 101
​ Name: count, dtype: int64
​

5. 离群值检测

任务介绍

  • 使用拉依达准则对data的特征Member years进行离群值检测；
  • 如果存在离群值，输出离群值的个数outlier_num，并将包含离群值的数据记录保存在变量outeliers中，并打印变量内容。

预期结果

补全代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import pandas as pd
import numpy as np

# 读取csv文件到DataFrame
data = pd.read_csv('user_review.csv')

# 提取'Member years'这一列
member_data = data[['Member years']]

'''
拉伊达准则
计算四分位数（Q1 和 Q3）：计算Member years特征的第25百分位数（Q1）和第75百分位数（Q3）。
计算IQR（Interquartile Range）：IQR = Q3 - Q1。
判断离群值：低于 Q1 - 1.5 * IQR 或高于 Q3 + 1.5 * IQR 的数据点视为离群值。
统计离群值的个数，并提取包含离群值的记录。
'''

# 计算四分位数
Q1 = member_data['Member years'].quantile(0.25)  # 第25百分位数
Q3 = member_data['Member years'].quantile(0.75)  # 第75百分位数

# 计算IQR（四分位间距）
IQR = Q3 - Q1

# 写出过滤条件：低于 Q1 - 1.5 * IQR 或 高于 Q3 + 1.5 * IQR 的值为离群值
outlier_judge = (member_data['Member years'] < (Q1 - 1.5 * IQR)) | (member_data['Member years'] > (Q3 + 1.5 * IQR))

# 统计离群值的个数
outlier_num = outlier_judge.sum()

# 提取包含离群值的样本记录
outliers = data[outlier_judge]

# 打印离群值记录
print(outliers)

​ User country User continent Member years Traveler type \
​ 75 USA North America -1806 Solo
​ 143 USA North America 13 Couples
​
​ Hotel name Hotel stars Nr. rooms Score
​ 75 Treasure Island- TI Hotel & Casino 4.0 2884 5
​ 143 Caesars Palace 5.0 3348 4
​