机器学习——第二次上机——波士顿房价预测任务（线性回归、岭回归实现）

发表于 2025-03-06 更新于 2025-06-12 分类于大二下，机器学习阅读次数：

波士顿房价预测任务（线性回归、岭回归实现）

包括数据准备、模型训练、模型评估与选择、性能度量、参数选择

问题背景与数据集介绍

波士顿房价预测是一个经典的机器学习任务，类似于程序员世界的“Hello World”。和大家对房价的普遍认知相同，波士顿地区的房价受诸多因素影响。美国某经济杂志登出波士顿房价数据集，该数据集包含506条观测信息，统计了13种可能影响房价的因素（输入变量）和该类型房屋的均价（输出变量），其中每条观测信息包含城镇犯罪率、一氧化氮浓度、住宅平均房间数、到中心区域的加权距离以及自住房平均房价等关于波士顿周边或者城镇房价的描述，期望通过分析影响波士顿房价的因素来构建房价预测模型。相关属性描述如下图所示，其中最后一项就是想要预测的房屋均价。

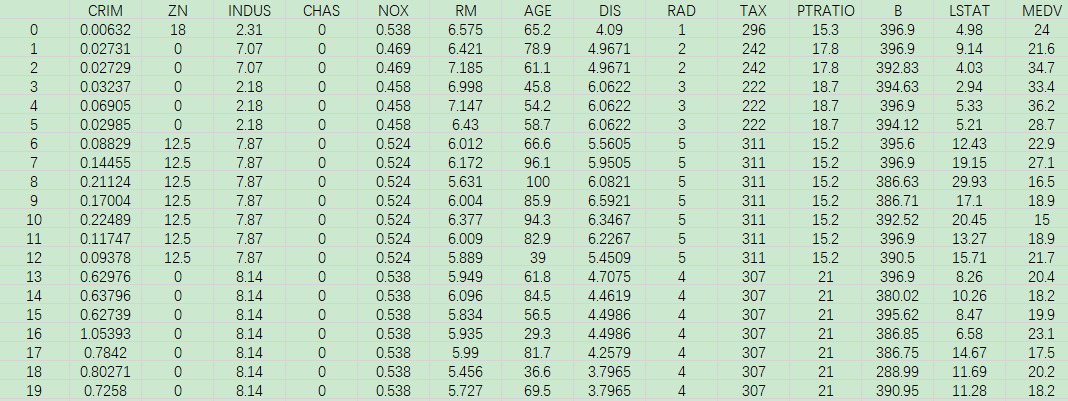
观测数据的示例如下图所示。

对于预测问题，可以根据预测输出的类型是连续的实数值，还是离散的标签，区分为回归任务和分类任务。因为房价是一个连续值，所以房价预测显然是一个回归任务。本次实验要求大家调用sklearn 的线性回归、岭回归模型来实现。

实现过程：

数据准备：导入数据、特征可视化
数据预处理：数据集划分、数据标准化处理
模型训练：线性回归、岭回归
模型评估与选择、参数选择

数据准备

导入数据

1
2
3

from sklearn.datasets import load_boston
boston = load_boston()
print(boston.DESCR)

数据可视化

通过观察不同属性与房价之间的关系，分析影响房价的主要因素。

boston.data 存储的是所有样本的属性值，boston.target 存储的是所有样本的房价。下段程序所展示的13幅图中，横坐标是该属性的取值，纵坐标是房价值。

# 导入matplotlib库中的pyplot模块，用于绘制图表
import matplotlib.pyplot as plt

# 设置图表的大小，figsize指定了图表的宽度和高度，单位是英寸
plt.figure(figsize=(20, 10))

# 遍历波士顿数据集的13个特征
for i in range(13):
    # 创建一个2行7列的子图，并在当前子图中绘制散点图
    plt.subplot(2, 7, i + 1)  # 2行7列的第i+1个子图
    
    # 绘制散点图：x轴是第i个特征，y轴是目标值（房价中位数），s指定点的大小
    plt.scatter(boston.data[:, i], boston.target, s=20)
    
    # 设置当前子图的标题，显示当前特征的名称
    plt.title(boston.feature_names[i])

# 保存当前图表为PNG格式的图片，文件名为img.png
plt.savefig('img.png')

# 显示绘制的所有子图
plt.show()

数据预处理

任务1：数据集划分

调用sklearn.model_selection中的train_test_split()函数，把boston数据集分为训练集和测试集，划分比例是4:1。

补全代码：

from sklearn.model_selection import train_test_split
import numpy as np
# 加载波士顿房价数据集
boston = load_boston()

# 将数据集划分为训练集和测试集，test_size=0.2 表示测试集占20%，即训练集占80%
X_train, X_test, y_train, y_test = train_test_split(boston.data, boston.target, test_size=0.2)

结果：

X_train：训练集的特征数据，形状为 (404, 13)，即 80% 的数据（506 * 0.8 = 404 个样本），每个样本有 13 个特征。
X_test：测试集的特征数据，形状为 (102, 13)，即 20% 的数据（506 * 0.2 = 102 个样本）。
y_train：训练集的目标值，形状为 (404,)，即对应训练集的 404 个房价中位数。
y_test：测试集的目标值，形状为 (102,)，即对应测试集的 102 个房价中位数。

总结：

train_test_split() 将数据集（包括特征和目标值）按照指定的比例随机划分为训练集和测试集。划分后的数据将用于模型的训练和评估，确保模型评估时使用的数据不会在训练过程中被“看见”。
test_size=0.2 表示将 20% 的数据作为测试集，80% 的数据作为训练集。
random_state=42 确保每次划分数据集时能得到一致的结果，保证实验的可复现性。

任务2：数据标准化处理：

1. Z-score标准化

首先使用StandardScaler()函数初始化对属性值的标准化器，然后调用fit_transform()方法对训练数据进行Z-score标准化，再将这个标准化器调用transform()方法用于测试数据的标准化。

补全代码：

from sklearn.preprocessing import StandardScaler
# 初始化对属性值的标准化器
ss_X = StandardScaler()
# ss_X调用fit_transform()和transform()方法对训练数据和测试数据进行标准化
# 对训练数据进行标准化，fit_transform() 方法会计算训练数据的均值和标准差，并应用到训练数据
# 训练数据X_train会被标准化为均值0，标准差1
X_train = ss_X.fit_transform(X_train)

# 对测试数据进行标准化，使用transform()方法来使用训练数据的均值和标准差来标准化测试数据
# 注意：测试数据不能再用fit_transform()，否则会使用测试数据的统计量，导致数据泄露
X_test = ss_X.transform(X_test)

Z-score 标准化的过程是将数据转换为均值为0，标准差为1的分布。StandardScaler() 是 scikit-learn 提供的标准化工具，它通过去掉均值并除以标准差来实现这一标准化。

代码解释：

对训练数据进行标准化：

1	X_train = ss_X.fit_transform(X_train)

- fit()：计算训练数据的均值和标准差。 - transform()：使用训练数据的均值和标准差将数据标准化。 - fit_transform()：这两个操作结合在一起，计算并转换训练数据，使其均值为0，标准差为1。

对测试数据进行标准化：

1	X_test = ss_X.transform(X_test)

- 对测试数据应用 transform() 方法时，不会重新计算均值和标准差，而是使用在训练数据上计算得到的均值和标准差对测试数据进行转换。 - 这确保了测试数据的标准化是基于训练数据的统计信息，而不是测试数据本身的统计信息。

2. MinMax标准化

补全代码：

from sklearn.preprocessing import MinMaxScaler
# 初始化对属性值的标准化器
mm_X = MinMaxScaler()
# mm_X调用fit_transform()和transform()方法对训练数据和测试数据进行MinMax标准化
X_train1 = mm_X.fit_transform(X_train)
X_test1 = mm_X.transform(X_test)

在 MinMax 标准化（也称为 归一化）中，数据将被缩放到指定的最小值和最大值之间，通常是将数据缩放到 [0, 1] 范围内。这对于那些对特征的绝对范围敏感的算法非常有效。

MinMaxScaler 是 scikit-learn 提供的一个标准化工具，它会将每个特征缩放到一个指定的范围内，默认情况下是 [0, 1]。

代码解释：

对训练数据进行 MinMax 标准化：

1	X_train1 = mm_X.fit_transform(X_train)

- fit_transform() 方法会计算训练数据的最小值和最大值，并将数据缩放到 [0, 1] 范围内。 - fit()：计算训练数据的最小值和最大值。 - transform()：根据计算出的最小值和最大值，进行数据的转换。 - fit_transform() 是这两个操作的组合，直接返回标准化后的训练数据。

对测试数据进行 MinMax 标准化：

1	X_test1 = mm_X.transform(X_test)

- transform() 方法会使用训练数据上的最小值和最大值来转换测试数据。 - 注意：transform() 仅仅使用训练数据的统计量（即最小值和最大值）来对测试数据进行标准化，避免了数据泄露问题。如果对测试数据使用 fit_transform()，就会导致模型从测试数据中学习统计量，破坏了训练和测试数据的独立性。

MinMax 标准化是一种常用的数据预处理方法，尤其适用于特征的取值范围差异较大时。它将每个特征的最小值映射到 0，最大值映射到 1，其他值则在该区间内按比例进行缩放。这样做的好处是避免了某些特征因数值范围较大而在训练模型时占据主导地位，尤其是对于需要计算距离或内积的模型，如 KNN、SVM 等，使用 MinMax 标准化后的数据会使模型训练更加稳定。

模型训练与评估

任务3.1：线性回归模型训练

调用sklearn.linear_model中的LinearRegression()函数，对训练集(X_train,y_train)进行模型训练，并预测测试集X_test的房价lr_y_predict。

补全代码：

from sklearn.linear_model import LinearRegression
# 初始化线性回归模型
lr = LinearRegression()
# 线性回归模型训练
lr.fit(X_train, y_train)  # 使用训练集数据训练模型

# 模型预测
lr_y_predict = lr.predict(X_test)  # 使用训练好的模型对测试集数据进行预测

代码解释：

训练模型：

1	lr.fit(X_train, y_train)

- fit() 方法会使用训练集数据 (X_train, y_train) 来训练线性回归模型。训练过程就是计算线性回归模型的系数（权重）和截距，以使预测值最接近真实目标值。

预测房价：

1	lr_y_predict = lr.predict(X_test)

- predict() 方法会使用已经训练好的模型来对测试集 X_test 进行预测，返回预测的房价（即预测值 lr_y_predict）。模型根据训练时学到的关系来预测测试集中的每个样本的房价。

任务3.2：线性回归模型评估

回归模型常用的三种评价指标：（1）R方分数（决定系数）、（2）MSE均方误差、以及（3）MAE平均绝对误差。

方法一：调用sklearn.metrics中的相关函数，计算测试结果lr_y_predict与真实结果y_test之间的误差或精度。

from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
print ('the value of R-squared of LR is',r2_score(y_test,lr_y_predict))
print ('the MSE of LR is',mean_squared_error(y_test,lr_y_predict))
print ('the MAE of LR is',mean_absolute_error(y_test,lr_y_predict))

the value of R-squared of LR is 0.7250808093832966
the MSE of LR is 23.56944609104811
the MAE of LR is 3.302381007591344

方法二：自己编写函数，计算上述指标。本实验要求学生至少完成MSE均方误差的计算，并打印输出结果。

# 请在下方作答
# 计算R²（决定系数）
def calculate_r2(y_true, y_pred):
    # R² = 1 - (SS_res / SS_tot)
    ss_res = ((y_true - y_pred) ** 2).sum()  # 残差平方和
    ss_tot = ((y_true - y_true.mean()) ** 2).sum()  # 总平方和
    r2_score = 1 - (ss_res / ss_tot)  # 决定系数
    return r2_score

# 计算MSE（均方误差）
def calculate_mse(y_true, y_pred):
    mse = mean_squared_error(y_true, y_pred)
    return mse

# 计算MAE（平均绝对误差）
def calculate_mae(y_true, y_pred):
    mae = mean_absolute_error(y_true, y_pred)
    return mae

# 评估模型
r2 = calculate_r2(y_test, lr_y_predict)  # R²
mse = calculate_mse(y_test, lr_y_predict)  # MSE
mae = calculate_mae(y_test, lr_y_predict)  # MAE

# 输出结果
print(f"R² (决定系数): {r2}")
print(f"MSE (均方误差): {mse}")
print(f"MAE (平均绝对误差): {mae}")

R² (决定系数): 0.7250808093832966
MSE (均方误差): 23.56944609104811
MAE (平均绝对误差): 3.302381007591344

下面是 R²（决定系数）、MSE（均方误差） 和 MAE（平均绝对误差） 的计算公式：

1. R²（决定系数）计算公式：

R² 衡量模型对目标变量变化的解释程度。它的取值范围为 0 到 1，越接近 1，表示模型越能解释数据的变异性。

公式: $$ R^2=1-\frac{\sum_{i=1}^{n}(y_i-\hat{y}_i)^2}{\sum_{i=1}^{n}(y_i-\bar{y})^2} $$

( $y_i $)：实际值（真实的目标值）。
( ŷ_i )：预测值（模型预测的目标值）。
( ȳ )：实际值的均值（ $\bar{y} = \frac{1}{n} \sum_{i=1}^{n} y_i$ ）。
( n )：样本数。

解释：

分子部分是 残差平方和（RSS），衡量预测值与真实值之间的差异。
分母部分是 总平方和（TSS），衡量真实值与均值之间的差异。
R² 越接近 1，表示模型的拟合度越好。

2. MSE（均方误差）计算公式：

MSE 衡量预测值与真实值之间差异的平方和的平均值，是一种常用的回归模型评估指标。

公式： $$ MSE = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 $$

( y_i )：实际值。
( ŷ_i)：预测值。
( n )：样本数。

解释：

MSE 是实际值与预测值之间差异的平方和的平均值，越小表示模型的预测误差越小。

3. MAE（平均绝对误差）计算公式：

MAE 衡量预测值与真实值之间差异的绝对值的平均值，也是一种常用的回归模型评估指标。

公式： $$ MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - \hat{y}_i| $$

( y_i )：实际值。
( ŷ_i )：预测值。
( n )：样本数。

解释：

MAE 是实际值与预测值之间差异的绝对值的平均值，越小表示模型的预测性能越好。

总结：

R²（决定系数）：度量模型拟合优度，越接近 1 表示模型越好。
MSE（均方误差）：越小，表示模型的预测误差越小。
MAE（平均绝对误差）：越小，表示模型在预测时的绝对误差越小。

任务3.3：岭回归模型训练

调用sklearn.linear_model中的Ridge()函数(参数设置为5)，对训练集(X_train,y_train)进行模型训练，并预测测试集X_test的房价rd_y_predict。

补全代码：

from sklearn.linear_model import Ridge
rd = Ridge(alpha=5)
#岭回归模型训练
rd.fit(X_train, y_train)
# 输出训练后的模型系数（回归系数）
print(rd.coef_)
#模型测试
rd_y_predict = rd.predict(X_test)

[-0.89921997  1.17687007  0.06847273  0.58380163 -2.09273127  2.39227753
  0.15081088 -3.06269707  2.53630955 -1.8549535  -2.24256957  0.89722135
 -3.79040179]

岭回归（Ridge Regression）

岭回归（Ridge Regression），又称 L2 正则化回归，是一种扩展了普通最小二乘回归（OLS）的回归模型。其核心思想是在最小化 残差平方和（即普通最小二乘回归的目标函数）的同时，加入一个 正则化项，用于惩罚模型的复杂性，避免过拟合。

岭回归的公式

岭回归的目标函数为： $$ \text{minimize} \quad \left( \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 + \alpha \sum_{j=1}^{p} \beta_j^2 \right) $$ 其中：

( y_i )：实际观测值。
( ŷ_i )：模型预测值。
( β_j )：模型的回归系数。
( α )：正则化强度（超参数），控制正则化项的权重。

关键点：

残差平方和：普通最小二乘回归的目标函数是最小化预测值和真实值之间的差异平方和：$\sum_{i=1}^{n} (y_i - \hat{y}_i)^2$
L2 正则化：岭回归在最小化残差平方和的同时，加上一个正则化项$ _{j=1}^{p} _j^2 $，用来限制回归系数的大小。这个正则化项惩罚过大的系数，使得系数趋向于 0，但不会完全为 0（与 Lasso 回归不同，Lasso 是 L1 正则化，会使部分系数变为 0）。
- $$：是岭回归的正则化参数，控制惩罚项的强度。较大的 ( ) 值会增加正则化的惩罚，使模型的系数变得较小，从而减少过拟合。

岭回归的作用

防止过拟合：在普通的最小二乘回归中，若特征非常多，模型可能会在训练数据上表现得非常好，但却在测试数据上表现得较差（过拟合）。通过在回归系数上施加惩罚，岭回归减少了模型的复杂度，从而帮助防止过拟合。
适应多重共线性：当特征之间存在强烈的相关性时（即多重共线性），普通的最小二乘回归可能无法得出稳定的回归系数。岭回归通过正则化项使得模型更稳定，避免共线性问题带来的不稳定性。

岭回归与普通最小二乘回归的区别

普通最小二乘回归：最小化残差平方和，没有对回归系数施加任何惩罚。因此，模型会根据训练数据的噪声来拟合训练数据，可能导致过拟合。
岭回归：最小化残差平方和，并加上正则化项，控制回归系数的大小，防止模型复杂度过高，减少过拟合。

岭回归的超参数 ( α )

( α )：是岭回归中的超参数，控制正则化项的强度。
- 当 ( = 0 ) 时，岭回归退化为普通的最小二乘回归。
- 当 ( ) 较大时，模型的回归系数被更多地惩罚，减少了过拟合的风险，但也可能导致欠拟合（即模型对数据的拟合能力不足）。

任务3.4：岭回归模型评估

与线性回归一样，岭回归模型有两种方法计算评价指标，这里调用sklearn.metrics来实现。

from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
print('the value of R-squared of Ridge is',r2_score(y_test,rd_y_predict ))
print('the MSE of Ridge is',mean_squared_error(y_test,rd_y_predict))
print('the MAE of Ridge is',mean_absolute_error(y_test,rd_y_predict))

the value of R-squared of Ridge is 0.7279447933421523
the MSE of Ridge is 23.323910246960786
the MAE of Ridge is 3.2535718613670053

参数选择

任务4：运用交叉验证选择模型参数

岭回归模型参数是正则化参数alpha，前面把它设置为5。为了选择最优参数，对训练集进行10次10折交叉验证。具体地，参数选择在[0,10]范围内，以1为步长，进行选择。 1. 总共进行11次实验（不同alpha值），每次实验将训练数据随机分成10份，重复10次； 2. 每一次划分，任意9份做训练，剩余1份测试，共执行10次，测试结果取平均； 3. 再将所有划分的结果再取平均，作为这一次alpha取值的分数； 4. 比较不同alpha取值的交叉验证模型分数，来选择其中表现最好的（分数最高的）模型的alpha值； 5. 用上述选择的alpha值对训练数据重新训练模型，再测试评估。

补全代码：

from sklearn.model_selection import cross_val_score 
from sklearn.model_selection import KFold


cv_score_list = []
for i in range(11):
    # alpha 取不同值
    rd = Ridge(alpha=i)
    avg_score_cross = []
    # 进行10次随机划分
    for j in range(10):
        #调用KFold()实现10折划分
        kf = KFold(n_splits=10, shuffle=True, random_state=j)
        #调用cross_val_score()计算训练集本次10折划分的分数
        score_cross = cross_val_score(rd, X_train, y_train, cv=kf, scoring='neg_mean_squared_error')
        avg_score_cross.append(np.mean(score_cross))
    cv_score_list.append(np.mean(avg_score_cross))

plt.plot(range(11), cv_score_list)
plt.show()

# cv_score_list中找到分数最大的模型所对应的alpha取值
index = np.argmax(cv_score_list)
rd = Ridge(alpha=index)
#岭回归模型训练
rd.fit(X_train, y_train)
#模型测试
rd_y_predict = rd.predict(X_test)
# 打印模型评估结果
from sklearn.metrics import mean_squared_error, mean_absolute_error
print(f"Best Alpha: {index}")
print(f"Mean Squared Error: {mean_squared_error(y_test, rd_y_predict)}")
print(f"Mean Absolute Error: {mean_absolute_error(y_test, rd_y_predict)}")

Best Alpha: 4
Mean Squared Error: 23.35986469628359
Mean Absolute Error: 3.260923268350155

二分类问题

任务5：波士顿房价二分类问题

为了了解分类问题的建模与评估，本任务将连续值的波士顿房价数值使用阈值进行二值化（0,1，例如：廉价房、品质房），可以将房价预测的回归问题，改为简单的二分类问题。

同样是包括四个步骤：数据准备、数据预处理、模型训练、模型评估与选择。

下面的程序使用方法一调用sklearn.metrics中的相应函数计算预测结果的准确率accuracy、f1 score、auc值。

from sklearn.datasets import load_boston
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, f1_score, roc_auc_score

boston = load_boston()
# 房价数值二值化
threshold = np.mean(boston.target)
labels = (boston.target>threshold).astype(np.int_)

# 数据集划分
X_train, X_test, y_train, y_test = train_test_split(boston.data, labels, test_size=0.2, random_state=42)
# 省略数据预处理步骤

# 模型训练
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
# 模型训练：我们使用 LogisticRegression（线性回归常用于回归问题，但 Logistic Regression 更适合于二分类问题）
lr = LogisticRegression(max_iter=10000)  # 设置最大迭代次数为10000以确保收敛

# 训练模型
lr.fit(X_train, y_train)

# 模型预测：对测试集进行预测
lr_y_predict = lr.predict(X_test)

# 模型评估
print('The accuracy score of LR is', accuracy_score(y_test, lr_y_predict))  # 准确率
print('The f1 score of LR is', f1_score(y_test, lr_y_predict))  # F1 分数
print('The auc of LR is', roc_auc_score(y_test, lr_y_predict))  # AUC（曲线下面积）

The accuracy score of LR is 0.9117647058823529
The f1 score of LR is 0.8695652173913043
The auc of LR is 0.89002079002079


f:\project python\.conda\lib\site-packages\sklearn\utils\deprecation.py:87: FutureWarning: Function load_boston is deprecated; `load_boston` is deprecated in 1.0 and will be removed in 1.2.

    The Boston housing prices dataset has an ethical problem. You can refer to
    the documentation of this function for further details.

    The scikit-learn maintainers therefore strongly discourage the use of this
    dataset unless the purpose of the code is to study and educate about
    ethical issues in data science and machine learning.

    In this special case, you can fetch the dataset from the original
    source::

        import pandas as pd
        import numpy as np

        data_url = "http://lib.stat.cmu.edu/datasets/boston"
        raw_df = pd.read_csv(data_url, sep="\s+", skiprows=22, header=None)
        data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
        target = raw_df.values[1::2, 2]

    Alternative datasets include the California housing dataset (i.e.
    :func:`~sklearn.datasets.fetch_california_housing`) and the Ames housing
    dataset. You can load the datasets as follows::

        from sklearn.datasets import fetch_california_housing
        housing = fetch_california_housing()

    for the California housing dataset and::

        from sklearn.datasets import fetch_openml
        housing = fetch_openml(name="house_prices", as_frame=True)

    for the Ames housing dataset.
  warnings.warn(msg, category=FutureWarning)

方法二：自己编写函数，计算上述指标。

本实验要求学生至少完成accuracy与f1 score的计算，并打印输出结果。

# 请在下方作答
from sklearn.metrics import confusion_matrix
# 计算准确率（Accuracy）
def calculate_accuracy(y_true, y_pred):
    correct = np.sum(y_true == y_pred)  # 计算正确预测的数量
    total = len(y_true)  # 总样本数
    accuracy = correct / total  # 准确率
    return accuracy

# 计算F1分数（F1 Score）
def calculate_f1_score(y_true, y_pred):
    cm = confusion_matrix(y_true, y_pred)
    # 提取混淆矩阵中的 TP, FP, FN
    tp = cm[1, 1]  # True Positives
    fp = cm[0, 1]  # False Positives
    fn = cm[1, 0]  # False Negatives
    precision = tp / (tp + fp) if (tp + fp) != 0 else 0
    recall = tp / (tp + fn) if (tp + fn) != 0 else 0
    # 计算 F1 分数
    f1 = 2 * (precision * recall) / (precision + recall) if (precision + recall) != 0 else 0
    return f1


accuracy = calculate_accuracy(y_test, lr_y_predict)
f1_score = calculate_f1_score(y_test, lr_y_predict)

# 输出结果
print(f"Accuracy: {accuracy}")
print(f"F1 Score: {f1_score}")

Accuracy: 0.9117647058823529
F1 Score: 0.8695652173913043

1. 准确率 (Accuracy)：

准确率是正确分类的样本数与总样本数之比。

公式： $$ \text{Accuracy} = \frac{\text{正确预测的数量}}{\text{总样本数}} $$

2. F1 分数 (F1 Score)：

F1 分数是准确率 (Precision) 和召回率 (Recall) 的调和平均数。

公式： $$ F1 = 2 \times \frac{\text{Precision} \times \text{Recall}}{\text{Precision} + \text{Recall}} $$ 其中： $$ \text{Precision} = \frac{\text{True Positive}}{\text{True Positive} + \text{False Positive}} $$

$$ \text{Recall} = \frac{\text{True Positive}}{\text{True Positive} + \text{False Negative}} $$

3. AUC (Area Under the Curve)：

AUC 是 ROC 曲线下面积，用于衡量分类模型的性能，范围在 0 到 1 之间，越接近 1，模型表现越好。AUC 是一个广泛使用的评估二分类问题模型的性能的指标。

波士顿房价预测任务（线性回归、岭回归实现）

问题背景与数据集介绍

实现过程：

数据准备

导入数据

数据可视化

数据预处理

任务1：数据集划分

结果：

总结：

任务2：数据标准化处理：

1. Z-score标准化

代码解释：

2. MinMax标准化

代码解释：

模型训练与评估

任务3.1：线性回归模型训练

代码解释：

任务3.2：线性回归模型评估

1. R²（决定系数） 计算公式：

解释：

2. MSE（均方误差） 计算公式：

解释：

3. MAE（平均绝对误差） 计算公式：

解释：

总结：

任务3.3：岭回归模型训练

岭回归（Ridge Regression）

岭回归的公式

关键点：

岭回归的作用

岭回归与普通最小二乘回归的区别

岭回归的超参数 ( α )

任务3.4：岭回归模型评估

参数选择

任务4：运用交叉验证选择模型参数

二分类问题

任务5：波士顿房价二分类问题

1. 准确率 (Accuracy)：

2. F1 分数 (F1 Score)：

3. AUC (Area Under the Curve)：

1. R²（决定系数）计算公式：

2. MSE（均方误差）计算公式：

3. MAE（平均绝对误差）计算公式：