机器学习——上机实验10--支持向量机

发表于 2025-04-15 更新于 2025-04-17 分类于大二下，机器学习阅读次数：

上机实验10–支持向量机

任务1：sklearn中的SVC与惩罚系数C

提供一份糖尿病患者数据集diabetes.csv，该数据集有768个数据样本，9个特征(最后一列为目标特征数据)，并且已经存入变量data。特征的具体信息如下：

特征名称	特征含义	取值举例
feature1	怀孕次数	6
feature2	2小时口服葡萄糖耐受实验中的血浆葡萄浓度	148
feature3	舒张压 (mm Hg)	72
feature4	三头肌皮褶厚度(mm)	35
feature5	2小时血清胰岛素浓度 (mu U/ml)	0
feature6	体重指数(weight in kg/(height in m)^2)	33.6
feature7	糖尿病谱系功能(Diabetes pedigree function)	0.627
feature8	年龄	50
class	是否患有糖尿病	1：阳性；0：阴性

主要任务如下： - 请先将数据使用sklearn中的StandardScaler进行标准化； - 然后使用sklearn中的svm.SVC支持向量分类器，构建支持向量机模型（所有参数使用默认参数），对测试集进行预测，将预测结果存为pred_y，并对模型进行评价； - 最后新建一个svm.SVC实例clf_new，并设置惩罚系数C=0.3，并利用该支持向量分类器对测试集进行预测，将预测结果存为pred_y_new，并比较两个模型的预测效果。

待补全代码

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report
from sklearn.svm import SVC

# 读取数据
data = pd.read_csv('diabetes.csv')

# 请在下方作答 #
# 将目标特征与其他特征分离
X = data.drop('class', axis=1)  
y = data['class']  

# 划分训练集train_X, train_y和测试集train_X, train_y
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size = .2, random_state = 0)

# 训练集标准化，返回结果为scaled_train_X
scaler = StandardScaler()
scaled_train_X = scaler.fit_transform(train_X)

# 构建支持向量机模型
clf = SVC()

# 模型训练
clf.fit(scaled_train_X, train_y)

# 测试集标准化
scaled_test_X = scaler.transform(test_X)

# 使用模型返回预测值
pred_y = clf.predict(scaled_test_X)

# 打印支持向量的个数，返回结果为列表，[-1标签的支持向量，+1标签的支持向量]
print(clf.n_support_)

# 使用classification_report函数进行模型评价
print(classification_report(test_y, pred_y))

# 构建惩罚系数C为0.3的模型，并与之前的模型做比较
clf_new = SVC(C=0.3)
clf_new.fit(scaled_train_X, train_y)
pred_y_new = clf_new.predict(scaled_test_X)

print(clf_new.n_support_)
print(classification_report(test_y, pred_y_new))

#调整惩罚系数C寻优

[187 180]

              precision    recall  f1-score   support

           0       0.82      0.90      0.86       107

           1       0.70      0.55      0.62        47

    accuracy                           0.79       154

   macro avg       0.76      0.73      0.74       154

weighted avg       0.78      0.79      0.78       154

[197 196]

              precision    recall  f1-score   support

           0       0.83      0.92      0.87       107

           1       0.75      0.57      0.65        47

    accuracy                           0.81       154

   macro avg       0.79      0.75      0.76       154

weighted avg       0.81      0.81      0.80       154

预期结果

任务2：SVC选定RBF核函数，并寻优核带宽参数gamma

在支持向量分类器中，核函数对其性能有直接的影响。已知径向基函数 RBF 及核矩阵元素为： K(x_i, x_j) = exp (−γ∥x_i − x_j∥²) 且对于核矩阵K，有K_ij = K(x_i, x_j).

主要任务如下： - 自定义函数实现径向基函数 rbf_kernel，要求输入参数为两个矩阵 X、Y，以及 gamma； - 利用rbf_kernel核函数，计算标准化后的训练集scaled_train_X的核矩阵，并存为 rbf_matrix； - 利用rbf_kernel核函数，训练支持向量分类器 clf，并预测标准化后的测试数据 scaled_test_X 的标签，最后评价模型效果。 > 提示：先计算各自的 Gram 矩阵，然后再使用 np.diag 提取对角线元素，使用 np.tile 将列表扩展成一个矩阵。

待补全代码

import numpy as np
# 请在下方作答 #
def rbf_kernel(X, Y, gamma=0.5):
    
    # 获取X和Y的大小
    num1 = X.shape[0]
    num2 = Y.shape[0]
    
    # 计算X和X^T的矩阵乘积
    gram_1 = X.dot(X.T)
    
    # 获取gram_1对角线位置的元素，组成大小(num1, 1)的列表，并将整个列表复制，扩展为(num1, num2)大小的矩阵component1
    component1 = np.tile(np.diag(gram_1).reshape(-1, 1), (1, num2))
    
    # 计算Y和Y^T的乘积
    gram_2 = Y.dot(Y.T)
     
    # 获取gram_2对角线位置的元素，组成(1, num2)的列表，并将整个列表复制，扩展为(num1, num2)大小的矩阵component2
    component2 = np.tile(np.diag(gram_2).reshape(1, -1), (num1, 1))
   
    # 计算2X和Y^T的内积 
    component3 = 2 * X.dot(Y.T)
  
    # 返回结果
    result = np.exp(gamma*(component3 - component1 - component2))
    return result

# 计算糖尿病患者训练数据集的核矩阵
rbf_matrix = rbf_kernel(scaled_train_X, scaled_train_X)

# 训练一个支持向量分类器
clf = SVC(kernel=rbf_kernel)
clf.fit(scaled_train_X, train_y)
pred_y = clf.predict(scaled_test_X)
print (clf.n_support_)
print (classification_report(test_y, pred_y))

# 调整gamma值寻找最优

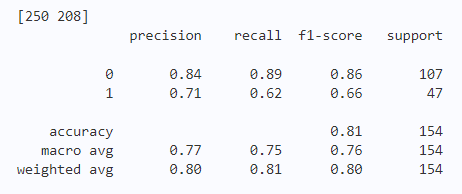
[250 208]

              precision    recall  f1-score   support

           0       0.84      0.89      0.86       107

           1       0.71      0.62      0.66        47

    accuracy                           0.81       154

   macro avg       0.77      0.75      0.76       154

weighted avg       0.80      0.81      0.80       154

预期结果

任务3：自定义函数实现SVM（选做）

主要任务如下： - 读取sklearn中的iris数据集，提取特征与标记，并进行数据划分为训练与测试集； - 自定义函数实现SVM； - 调用SVM函数进行支持向量机训练，并对测试集进行测试。

待补全代码

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

def create_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df['label'] = iris.target
    df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    data = np.array(df.iloc[:100, [0, 1, -1]])
    for i in range(len(data)):
        if data[i,-1] == 0:
            data[i,-1] = -1
    # print(data)
    return data[:,:2], data[:,-1]

# 读取数据，拆分数据，训练测试集划分
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)

class SVM:
    def __init__(self, max_iter=100, kernel='linear'):
        self.max_iter = max_iter
        self._kernel = kernel
    
    def init_args(self, features, labels):
        self.m, self.n = features.shape
        self.X = features
        self.Y = labels
        self.b = 0.0
        
        # 将Ei保存在一个列表里
        self.alpha = np.ones(self.m)
        self.E = [self._E(i) for i in range(self.m)]
        # 松弛变量
        self.C = 1.0
        
    def _KKT(self, i):
        y_g = self._g(i)*self.Y[i]
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1
    
    # g(x)预测值，输入xi（X[i]）
    def _g(self, i):
        r = self.b
        for j in range(self.m):
            r += self.alpha[j] * self.Y[j] * self.kernel(self.X[j], self.X[i])
        return r
    
    # 核函数
    def kernel(self, x1, x2):
        if self._kernel == 'linear':
            return np.dot(x1, x2)
        elif self._kernel == 'poly':
            return (sum([x1[k]*x2[k] for k in range(self.n)]) + 1)**2
    
        return 0
    
    # E（x）为g(x)对输入x的预测值和y的差
    def _E(self, i):
        return self._g(i) - self.Y[i]
    
    def _init_alpha(self):
        # 外层循环首先遍历所有满足0<a<C的样本点，检验是否满足KKT
        index_list = [i for i in range(self.m) if 0 < self.alpha[i] < self.C]
        # 否则遍历整个训练集
        non_satisfy_list = [i for i in range(self.m) if i not in index_list]
        index_list.extend(non_satisfy_list)
        
        for i in index_list:
            if self._KKT(i):
                continue
            
            E1 = self.E[i]
            # 如果E2是+，选择最小的；如果E2是负的，选择最大的
            if E1 >= 0:
                j = min(range(self.m), key=lambda x: self.E[x])
            else:
                j = max(range(self.m), key=lambda x: self.E[x])
            return i, j
        
    def _compare(self, _alpha, L, H):
        if _alpha > H:
            return H
        elif _alpha < L:
            return L
        else:
            return _alpha      
    
    def fit(self, features, labels):
        self.init_args(features, labels)
        
        for t in range(self.max_iter):
            # train
            i1, i2 =self._init_alpha()
            
            # 边界
            if self.Y[i1] == self.Y[i2]:
                L = max(0, self.alpha[i1]+self.alpha[i2]-self.C)
                H = min(self.C, self.alpha[i1]+self.alpha[i2])
            else:
                L = max(0, self.alpha[i2]-self.alpha[i1])
                H = min(self.C, self.C+self.alpha[i2]-self.alpha[i1])
                
            E1 = self.E[i1]
            E2 = self.E[i2]
            # eta=K11+K22-2K12
            eta = self.kernel(self.X[i1], self.X[i1]) + \
                  self.kernel(self.X[i2], self.X[i2]) - \
                  2 * self.kernel(self.X[i1], self.X[i2])
            if eta <= 0:
                # print('eta <= 0')
                continue
                
            alpha2_new_unc = self.alpha[i2] + self.Y[i2] * (E2 - E1) / eta
            alpha2_new = self._compare(alpha2_new_unc, L, H)
            
            alpha1_new = self.alpha[i1] + self.Y[i1] * self.Y[i2] * (self.alpha[i2] - alpha2_new)
            
            b1_new = -E1 - self.Y[i1] * self.kernel(self.X[i1], self.X[i1]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i1]) * (alpha2_new-self.alpha[i2])+ self.b 
            b2_new = -E2 - self.Y[i1] * self.kernel(self.X[i1], self.X[i2]) * (alpha1_new-self.alpha[i1]) - self.Y[i2] * self.kernel(self.X[i2], self.X[i2]) * (alpha2_new-self.alpha[i2])+ self.b 
            
            if 0 < alpha1_new < self.C:
                b_new = b1_new
            elif 0 < alpha2_new < self.C:
                b_new = b2_new
            else:
                # 选择中点
                b_new = (b1_new + b2_new) / 2
                
            # 更新参数
            self.alpha[i1] = alpha1_new
            self.alpha[i2] = alpha2_new
            self.b = b_new
            
            self.E[i1] = self._E(i1)
            self.E[i2] = self._E(i2)
        return 'train done!'
            
    def predict(self, data):
        r = self.b
        for i in range(self.m):
            r += self.alpha[i] * self.Y[i] * self.kernel(self.X[i], data)
            
        return 1 if r > 0 else -1
    
    def score(self, X_test, y_test):
        right_count = 0
        for i in range(len(X_test)):
            result = self.predict(X_test[i])
            if result == y_test[i]:
                right_count += 1
        return right_count / len(X_test)
    
    def _weight(self):
        # linear model
        yx = self.Y.reshape(-1, 1)*self.X
        self.w = np.dot(self.alpha, yx)
        return self.w

# 调用SVM进行模型训练与测试评估
svm = SVM(max_iter=100)
svm.fit(X_train, y_train)
svm.score(X_test, y_test)

0.92