机器学习——上机实验11--核化分类器判定西瓜好坏

发表于 更新于 分类于 ， 阅读次数：

上机实验11：核化分类器判定西瓜好坏

1
2
3
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
1
2
data = pd.read_csv("work/西瓜数据集3.0α.txt")
data
1
2
3
4
5
6
7
8
9
yes = data[data['Good melon'].isin(['是'])]
no = data[data['Good melon'].isin(['否'])]
fig, ax = plt.subplots(figsize=(12, 8))
ax.scatter(yes['Density'], yes['Sugar content'], marker='o', c='b', label='Yes')
ax.scatter(no['Density'], no['Sugar content'], marker='x', c='r', label='No')
ax.legend()
ax.set_xlabel('Density')
ax.set_ylabel('Sugar content')
plt.show() # 可以发现线性不可分
output_3_0

任务1：SVM分类器判定西瓜好坏

在SVM分类器中，使用线性核与高斯核进行比较。

1
2
3
4
5
from sklearn import svm

# 使用线性核与高斯核进行比较
linear_svc = svm.SVC(kernel='linear')  # 线性核
rbf_svc = svm.SVC(kernel='rbf')        # 高斯核（RBF）
1
2
3
temp = {'是': 1, '否': -1}
X = np.array(data.iloc[:, :2])
y = np.array(data.iloc[:, 2].replace(temp))[None].T
1
2
3
4
linear_svc.fit(X, y)
linear_svc.score(X,y)
# 查看支持向量
linear_svc.support_vectors_
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/sklearn/utils/validation.py:760: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
  y = column_or_1d(y, warn=True)





array([[0.666, 0.091],
       [0.243, 0.267],
       [0.343, 0.099],
       [0.639, 0.161],
       [0.657, 0.198],
       [0.36 , 0.37 ],
       [0.593, 0.042],
       [0.719, 0.103],
       [0.697, 0.46 ],
       [0.774, 0.376],
       [0.634, 0.264],
       [0.608, 0.318],
       [0.556, 0.215],
       [0.403, 0.237],
       [0.481, 0.149],
       [0.437, 0.211]])
1
2
3
4
rbf_svc.fit(X, y)
rbf_svc.score(X,y)
# 查看支持向量
rbf_svc.support_vectors_
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/sklearn/utils/validation.py:760: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
  y = column_or_1d(y, warn=True)

array([[0.666, 0.091],
       [0.243, 0.267],
       [0.245, 0.057],
       [0.343, 0.099],
       [0.639, 0.161],
       [0.657, 0.198],
       [0.36 , 0.37 ],
       [0.593, 0.042],
       [0.719, 0.103],
       [0.697, 0.46 ],
       [0.774, 0.376],
       [0.634, 0.264],
       [0.608, 0.318],
       [0.556, 0.215],
       [0.403, 0.237],
       [0.481, 0.149],
       [0.437, 0.211]])

任务2：Kernel Logistic Regression 判定西瓜好坏

将原始的Logistic Regression 进行核化，使用不同的核函数进行比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130

import matplotlib.colors as colors
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd


class LogisticRegression:
    kern_param = 0
    X = np.array([])
    a = np.array([])
    kernel = None

    def __init__(self, kernel='poly', kern_param=None):
        if kernel == 'poly':
            self.kernel = self.__linear__
            if kern_param:
                self.kern_param = kern_param
            else:
                self.kern_param = 1
        elif kernel == 'gaussian':
            self.kernel = self.__gaussian__
            if kern_param:
                self.kern_param = kern_param
            else:
                self.kern_param = 0.1
        elif kernel == 'laplace':
            self.kernel = self.__laplace__
            if kern_param:
                self.kern_param = kern_param
            else:
                self.kern_param = 0.1

    def fit(self, X, y, max_rate=100, min_rate=0.001, gd_step=10, epsilon=0.0001):
        m = len(X)
        self.X = np.vstack([X.T, np.ones(m)]).T
        # Construct kernel matrix
        K =self.kernel(self.X, self.X, self.kern_param)  # 填空1：计算核矩阵
        # Gradient descent
        self.a = np.zeros([m])
        prev_cost = 0
        next_cost = self.__cost__(K, y, self.a)
        while np.fabs(prev_cost-next_cost) > epsilon:
            neg_grad = -self.__gradient__(K, y, self.a)
            best_rate = rate = max_rate
            min_cost = self.__cost__(K, y, self.a)
            while rate >= min_rate:
                cost = self.__cost__(K, y, self.a+neg_grad*rate)
                if cost < min_cost:
                    min_cost = cost
                    best_rate = rate
                rate /= gd_step
            self.a += neg_grad * best_rate
            prev_cost = next_cost
            next_cost = min_cost

    def predict(self, X):
        # 1. 添加偏置项（与训练数据处理一致）
        X = np.vstack([X.T, np.ones(len(X))]).T  # 形状变为 (n_samples, n_features + 1)
        
        # 2. 计算核矩阵（训练数据与测试数据之间的核函数值）
        K = self.kernel(self.X, X, self.kern_param)  # 形状：(训练样本数, 测试样本数)
        
        # 3. 计算预测得分（关键修正：移除 self.Y 的乘法）
        pred = np.dot(self.a, K) 
        
        # 4. Sigmoid转换为概率并二值化
        prob = self.__sigmoid__(pred)
        return (prob >= 0.5).astype(int)

    # Kernels
    @staticmethod
    def __linear__(a, b, parameter):
        return np.dot(a, np.transpose(b))

    @staticmethod
    def __gaussian__(a, b, kern_param):
        mat = np.zeros([len(a), len(b)])
        for i in range(0, len(a)):
            for j in range(0, len(b)):
                mat[i][j] = np.exp(-np.sum(np.square(np.subtract(a[i], b[j]))) / (2 * kern_param * kern_param))
        return mat

    @staticmethod
    def __laplace__(a, b, kern_param):
        mat = np.zeros([len(a), len(b)])
        for i in range(0, len(a)):
            for j in range(0, len(b)):
                mat[i][j] = np.exp(-np.linalg.norm(np.subtract(a[i], b[j])) / kern_param)
        return mat

    @staticmethod
    def __sigmoid__(X):
        return np.exp(X) / (1 + np.exp(X))

    @staticmethod
    def __cost__(K, y, a):
        return -np.dot(y, np.dot(a, K)) + np.sum(np.log(1 + np.exp(np.dot(a, K))))

    @classmethod
    def __gradient__(cls, K, y, a):
        return -np.dot(K, y - cls.__sigmoid__(np.dot(a, K)))


# Read data
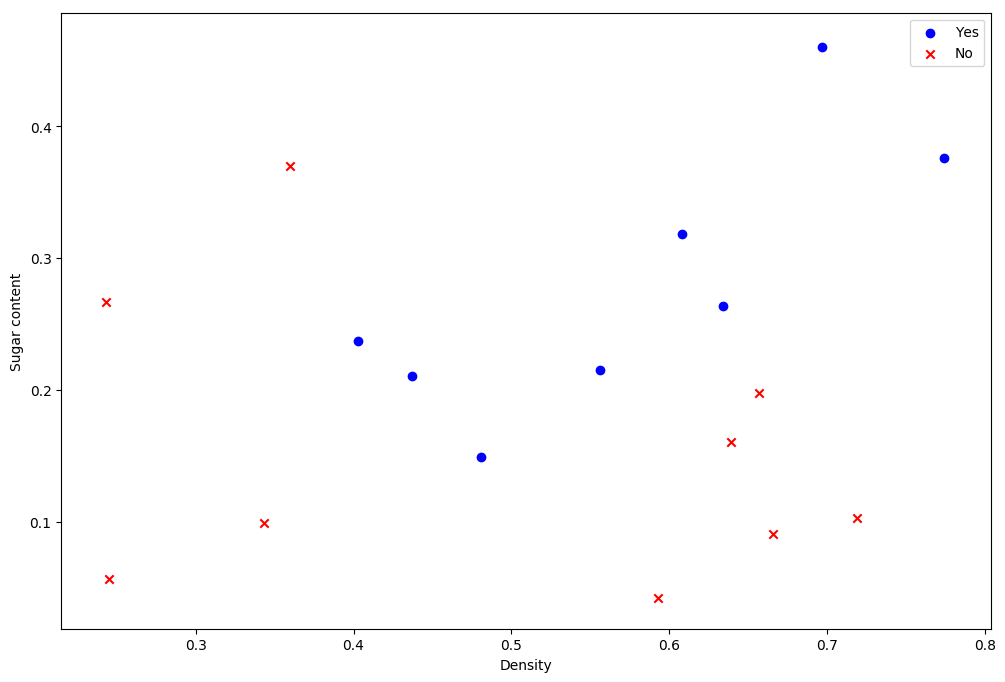
data = pd.read_csv("work/西瓜数据集3.0α.txt")
X = np.array(data[['Density', 'Sugar content']])
y = np.array(data['Good melon']) == '是'

# Kernels
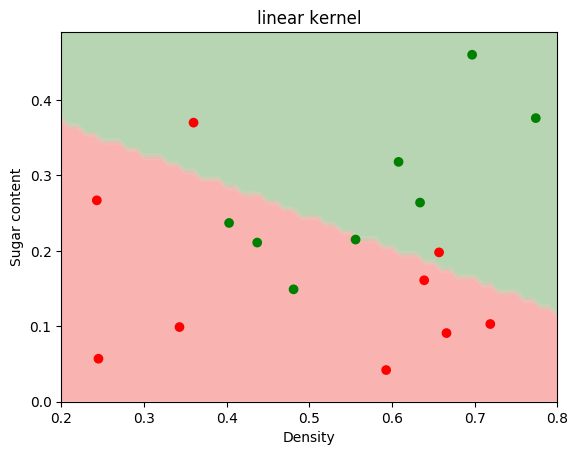
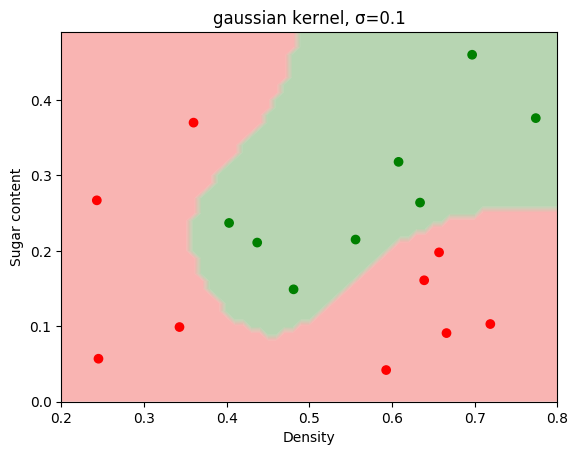
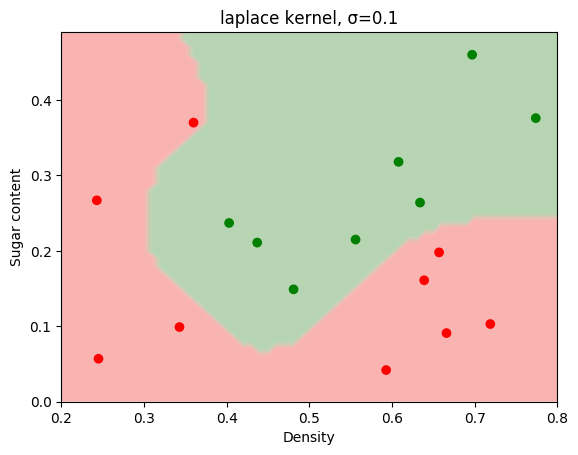
kernels = ['poly', 'gaussian', 'laplace']
titles = ['linear kernel', 'gaussian kernel, σ=0.1', 'laplace kernel, σ=0.1']

for i in range(0, len(kernels)):
    # Training
    # 填空3：实例化并训练模型
    model = LogisticRegression(kernel=kernels[i])
    model.fit(X, y)
    
    # Plot
    cmap = colors.LinearSegmentedColormap.from_list('watermelon', ['red', 'green'])
    xx, yy = np.meshgrid(np.arange(0.2, 0.8, 0.01), np.arange(0.0, 0.5, 0.01))
    Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.contourf(xx, yy, Z, cmap=cmap, alpha=0.3, antialiased=True)
    plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap)
    plt.xlabel('Density')
    plt.ylabel('Sugar content')
    plt.title(titles[i])
    plt.show()
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/ipykernel_launcher.py:97: RuntimeWarning: overflow encountered in exp
output_10_1
output_10_2
output_10_3

1. 线性核（Linear Kernel）

  • 数学形式：
    [ K(x_i, x_j) = x_i^T x_j + c (c ) ]
  • 特点：
    • 直接计算特征向量的内积，不进行非线性映射。
    • 决策边界为线性超平面，计算效率高。
  • 适用场景：
    • 数据线性可分（如两类可通过一条直线/平面分开）。
    • 特征维度较高时（避免核方法的计算开销）。
  • 西瓜数据集表现：
    • 生成直线决策边界，可能误分类非线性分布的样本。

2. 高斯核（Gaussian/RBF Kernel）

  • 数学形式：
    [ K(x_i, x_j) = (-|x_i - x_j|^2) (> 0) ]
  • 特点：
    • 基于样本间的欧氏距离（L2距离），隐式映射到无限维空间。
    • 参数 γ 控制影响范围：γ 越大，局部性越强（对邻近点更敏感）。
  • 适用场景：
    • 数据非线性可分（如环形分布、复杂流形）。
    • 特征维度较低或中等时效果最佳。
  • 西瓜数据集表现：
    • 生成平滑的非线性边界，能捕捉密度与含糖量的复杂交互关系。

3. 拉普拉斯核（Laplace Kernel）

  • 数学形式：
    [ K(x_i, x_j) = (-|x_i - x_j|_1) (> 0) ]
  • 特点：
    • 基于曼哈顿距离（L1距离），对异常值鲁棒性更强。
    • 隐式映射到无限维空间，但形状更尖锐（适合非光滑边界）。
  • 适用场景：
    • 数据分布不规则或存在离群点。
    • 特征具有稀疏性（如文本分类）。
  • 西瓜数据集表现：
    • 生成尖锐的非线性边界，可能更好地处理边缘样本。

以下是欧氏距离（Euclidean Distance）与曼哈顿距离（Manhattan Distance）的详细对比：

1. 数学定义

距离类型 公式 几何意义
欧氏距离 ( |x - y|_2 = ) 两点之间的直线距离
曼哈顿距离 ( |x - y|1 = {i=1}^n x_i - y_i

5. 选择建议

  • 优先欧氏距离：
    数据分布连续、特征维度较低、需要捕捉局部相似性时（如图像分类）。
  • 优先曼哈顿距离：
    数据稀疏（如文本）、存在噪声或异常值、特征维度较高时（如推荐系统）。

示例对比

假设两点 ( A(1, 1) ) 和 ( B(4, 5) )：

  • 欧氏距离：
    [ = 5 ]
  • 曼哈顿距离：
    [ |4-1| + |5-1| = 3 + 4 = 7 ]

总结

  • 欧氏距离：强调“直线最短”，适合低维连续数据。
  • 曼哈顿距离：强调“网格路径”，适合高维稀疏数据。
  • 在核函数中的体现：
    • 高斯核通过欧氏距离捕捉平滑边界，拉普拉斯核通过曼哈顿距离增强鲁棒性。