Zhang XiJun

邀请好友机制调研

发表于 2025-09-21 分类于实习， Tosea.ai

邀请码

邀请链接

在表里面增加一个邀请链接的字段，每个用户有专属的邀请链接

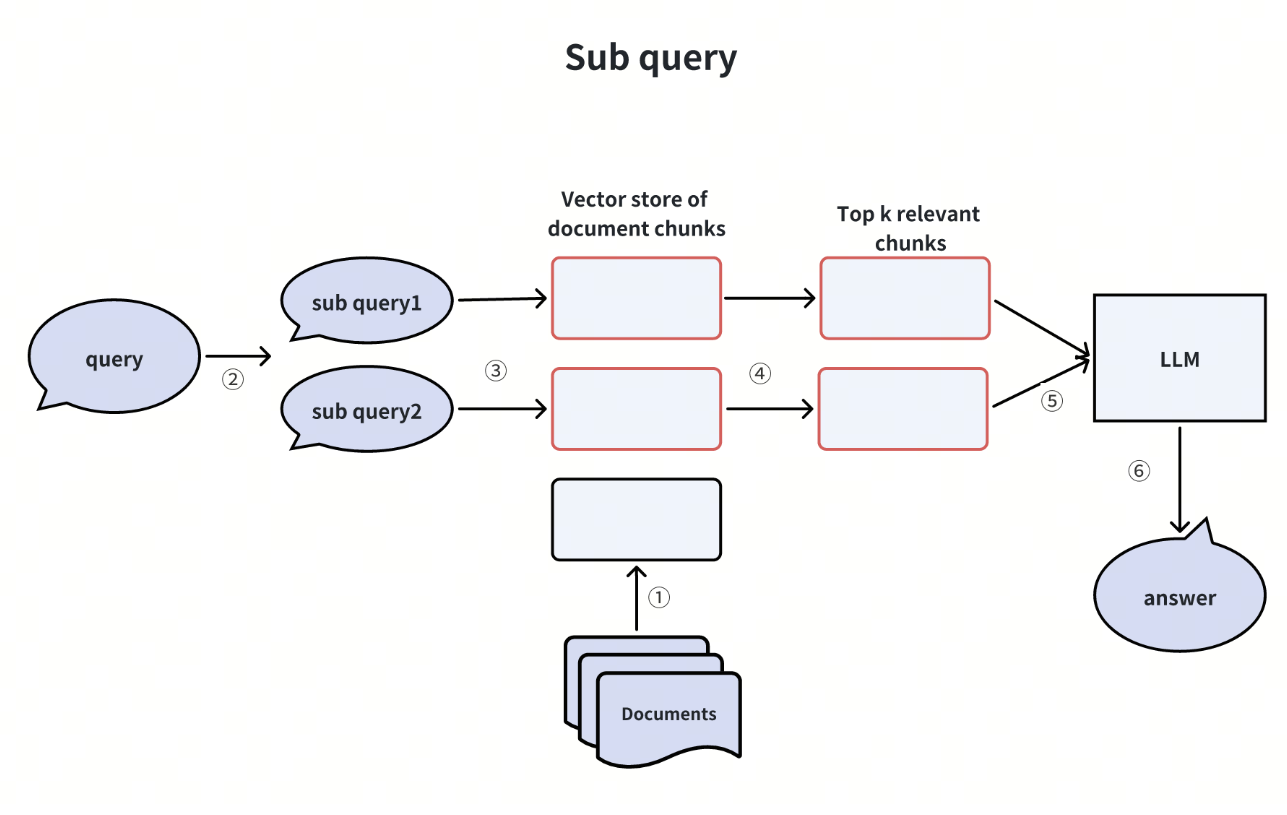
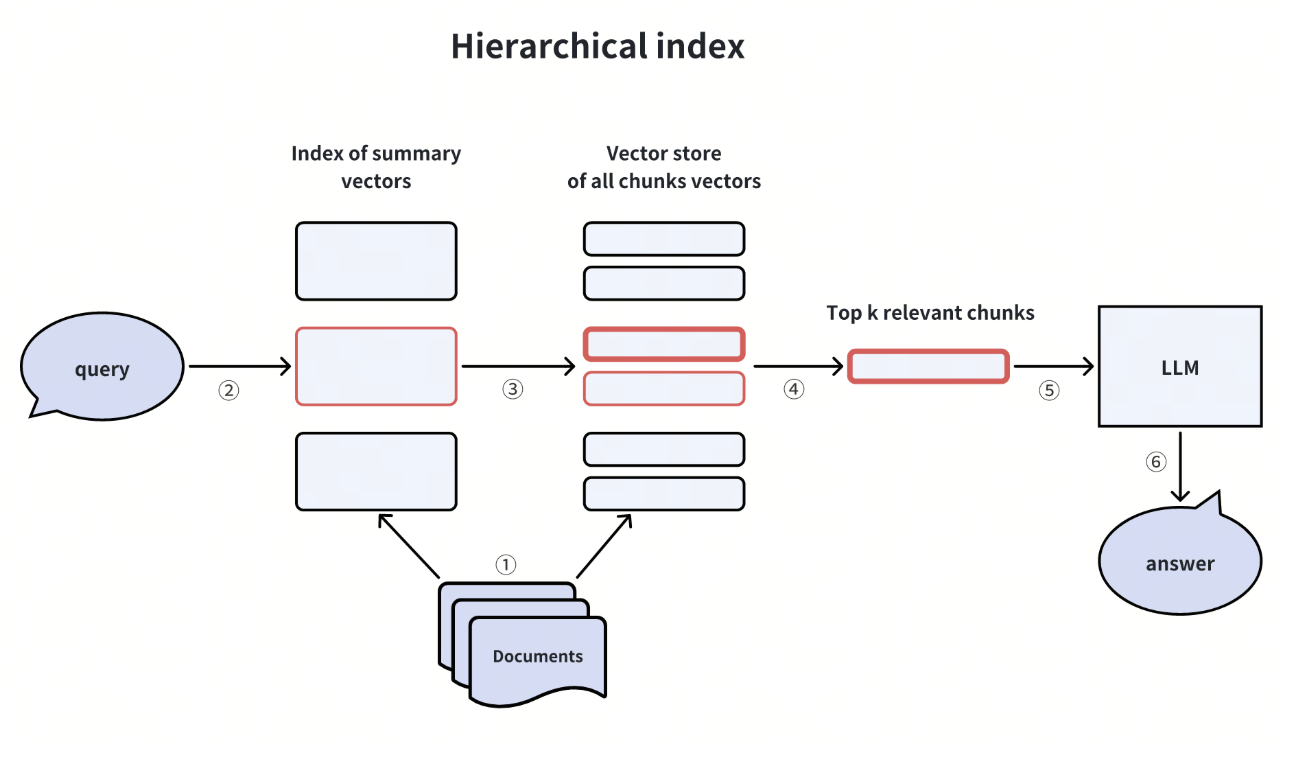
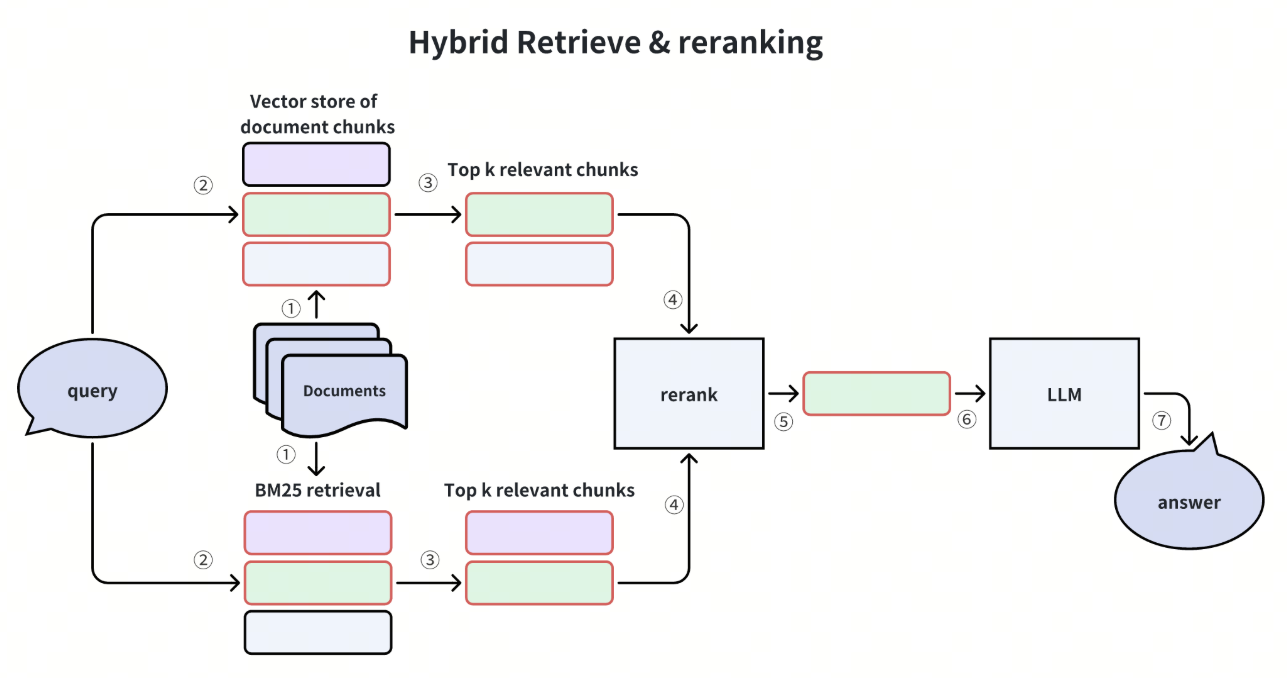
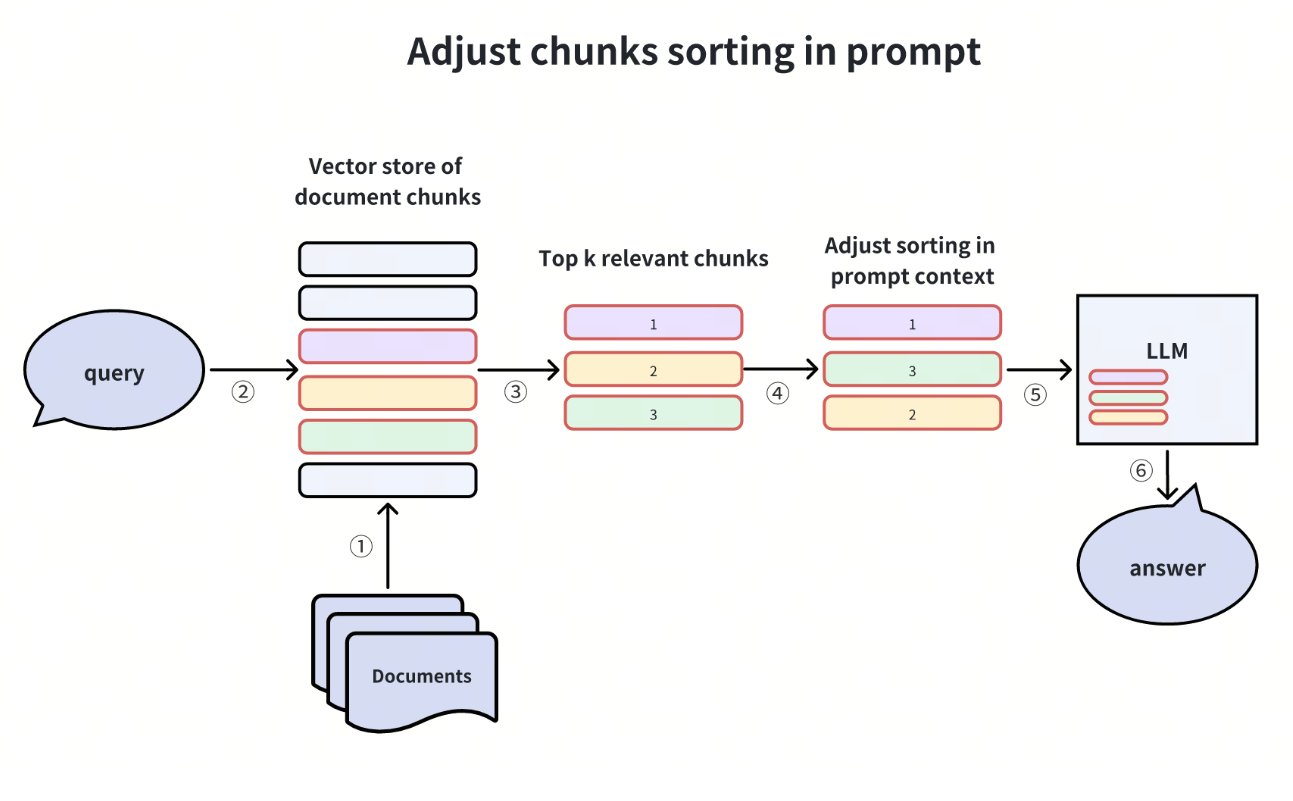
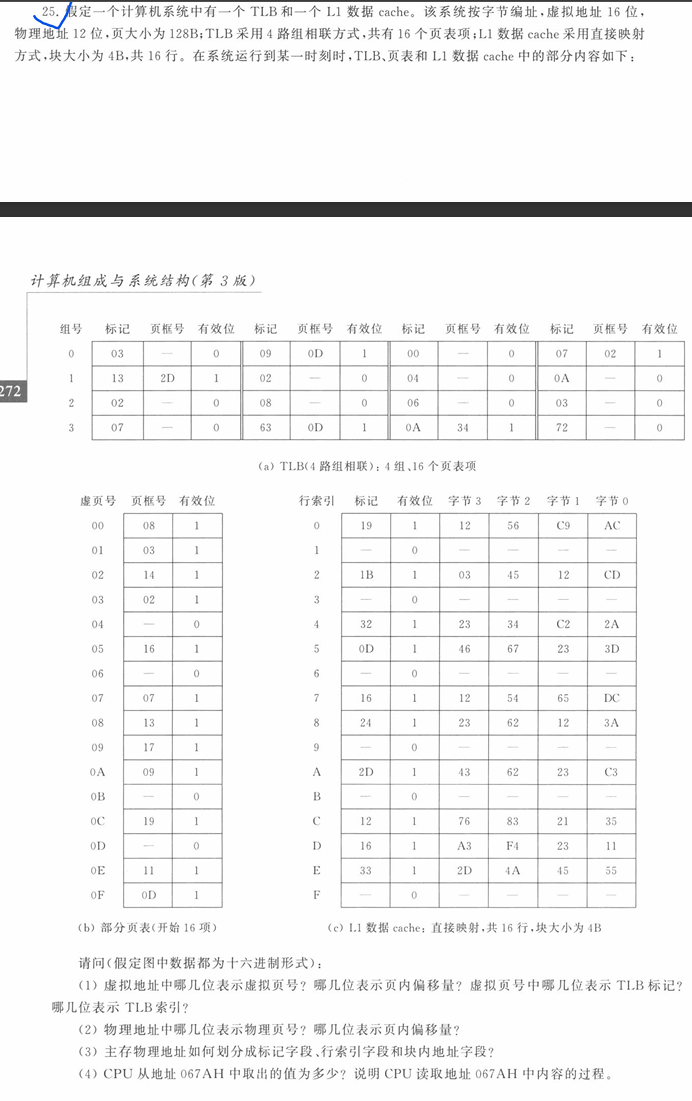
数据挖掘作业

发表于 2025-09-21 更新于 2025-11-17 分类于大三上，数据挖掘

数据的规范化

Min-Max 归一化（Normalization）

from sklearn.preprocessing import MinMaxScaler

# 公式: X_scaled = (X - X_min) / (X_max - X_min)
scaler = MinMaxScaler()
X_norm = scaler.fit_transform(X)

结果范围：[0, 1]（或可指定其他范围）
保留原始分布形状
对异常值敏感（因为依赖最大/最小值）

Z-score 标准化（Standardization）

from sklearn.preprocessing import StandardScaler

# 公式: X_scaled = (X - μ) / σ
scaler = StandardScaler()
X_std = scaler.fit_transform(X)

结果：均值 ≈ 0，标准差 ≈ 1
不保证固定范围（可能有 -3 到 +3 甚至更大）
对异常值相对稳健

RobustScaler (鲁棒标准化)与Z-score 标准化（Standardization）对比

StandardScaler (Z-score标准化)

公式: (x - 均值) / 标准差

问题: 均值和标准差都会被异常值严重影响！

例如:
正常值: [100, 150, 200, 180, 220]  → 均值 = 170
加入异常值: [100, 150, 200, 180, 220, 6445]  → 均值 = 1216 ❌

结果: 所有正常值都变成负数，异常值主导了整个标准化过程

RobustScaler (鲁棒标准化)

公式: (x - 中位数) / IQR
其中 IQR = Q3 - Q1 (四分位距)

优势: 中位数和IQR不受异常值影响！

例如:
正常值: [100, 150, 200, 180, 220]  → 中位数 = 180, IQR = 70
加入异常值: [100, 150, 200, 180, 220, 6445]  → 中位数 = 190, IQR = 70 ✅

结果: 异常值不会扭曲正常数据的标准化结果

Apriori算法

Apriori 算法 是一种用于 频繁项集挖掘（Frequent Itemset Mining） 和 关联规则学习（Association Rule Learning） 的经典算法。

Apriori 基于一个非常重要的性质，叫 先验性质（Apriori Property）：

如果一个项集是频繁的，那么它的所有子集也一定是频繁的。 反过来：如果一个项集是非频繁的，那么它的所有超集也一定是非频繁的。

这个性质可以用来 剪枝（prune），避免穷举所有可能的组合。

Apriori 的 候选生成规则：

当且仅当它们的前 (k-1) 个项相同，两个频繁 k项集才可以连接生成 (k+1)项集。

剪枝规则只有一句话：

对候选 k-项集 c，只要存在任何一个 (k−1)-子集不在 Lₖₖ₋₁ 里，就把 c 整集扔掉，不再给它计数。

为什么这样做合法？

基于 Apriori 向下封闭性（频繁项集的所有子集必频繁）。若 c 哪怕只有一个 (k−1)-子集是非频繁的，c 自己绝对不可能频繁，所以没必要浪费一次数据库扫描去数它的支持度。

例子

transactions = [
    ['牛奶', '面包', '黄油'],
    ['牛奶', '面包'],
    ['牛奶', '可乐'],
    ['面包', '黄油'],
    ['牛奶', '面包', '可乐'],
]

我们的目标是找出 频繁项集（比如哪些商品经常一起出现）。

步骤 1：设定最小支持度（min_support）

假设我们设 min_support = 2，意思是：至少出现在 2 个购物篮中才算“频繁”。

支持度（Support） = 包含该项集的交易数 / 总交易数
这里我们直接用“出现次数 ≥ 2”来简化。

步骤 2：生成 1-项集（单个商品）

统计每个商品出现次数：

项集	出现次数
{‘牛奶’}	4
{‘面包’}	4
{‘黄油’}	2
{‘可乐’}	2

全部 ≥2 → 都是频繁 1-项集。

步骤 3：生成 2-项集（两两组合）

从频繁 1-项集中两两组合（注意：只组合那些“所有子集都频繁”的）：

可能的组合： - {‘牛奶’, ‘面包’} - {‘牛奶’, ‘黄油’} - {‘牛奶’, ‘可乐’} - {‘面包’, ‘黄油’} - {‘面包’, ‘可乐’} - {‘黄油’, ‘可乐’}

现在统计它们在交易中出现的次数：

项集	出现次数
{‘牛奶’, ‘面包’}	3 ✅
{‘牛奶’, ‘黄油’}	1 ❌
{‘牛奶’, ‘可乐’}	2 ✅
{‘面包’, ‘黄油’}	2 ✅
{‘面包’, ‘可乐’}	1 ❌
{‘黄油’, ‘可乐’}	0 ❌

保留 ≥2 的 → 频繁 2-项集： - {‘牛奶’, ‘面包’} - {‘牛奶’, ‘可乐’} - {‘面包’, ‘黄油’}

步骤 4：生成 3-项集

从频繁 2-项集中尝试组合。
比如：{‘牛奶’,‘面包’} 和 {‘牛奶’,‘可乐’} → 可以组合成 {‘牛奶’,‘面包’,‘可乐’}
但必须检查它的所有 2-项子集是否都在频繁 2-项集中：

子集：{‘牛奶’,‘面包’} ✅
子集：{‘牛奶’,‘可乐’} ✅
子集：{‘面包’,‘可乐’} ❌（之前被剪掉了！）

→ 所以 {‘牛奶’,‘面包’,‘可乐’} 不合法，不能生成。

再试：{‘牛奶’,‘面包’} + {‘面包’,‘黄油’} → {‘牛奶’,‘面包’,‘黄油’}
检查子集： - {‘牛奶’,‘面包’} ✅ - {‘牛奶’,‘黄油’} ❌（之前只有1次） - {‘面包’,‘黄油’} ✅

→ 有一个子集不频繁 → 整个 3-项集被剪枝！

结论：没有频繁 3-项集。

算法结束。

FP-growth

FP-growth（Frequent Pattern Growth）算法，它是一种用于频繁项集挖掘的高效算法

Apriori 算法：通过逐层生成候选项集（先1项，再2项…），每次都要扫描整个数据库，效率低。
FP-growth：不生成候选项集，而是构建一种压缩数据结构——FP树（Frequent Pattern Tree），只需扫描数据库 2 次，效率更高！

FP-growth 的核心思想（分两步）

第一步：构建 FP 树（FP-Tree）

第一次扫描：统计每个单项的支持度，过滤掉低于 min_support 的项。
对每条事务：
- 只保留频繁项
- 按支持度从高到低排序
第二次扫描：将排序后的事务插入 FP 树。

第二步：从 FP 树中挖掘频繁项集

从支持度最低的频繁项开始（称为“后缀模式”）
对每个项，找出它的条件模式基（Conditional Pattern Base）
构建条件 FP 树（Conditional FP-Tree）
递归挖掘，直到树为空

补充.4 关联_FP算法_哔哩哔哩_bilibili

模型评价指标

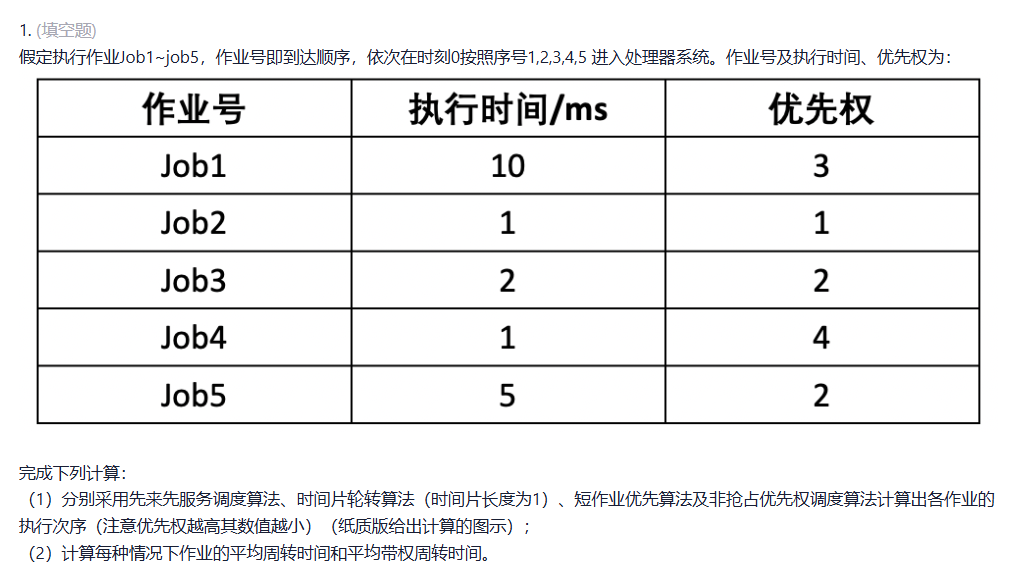
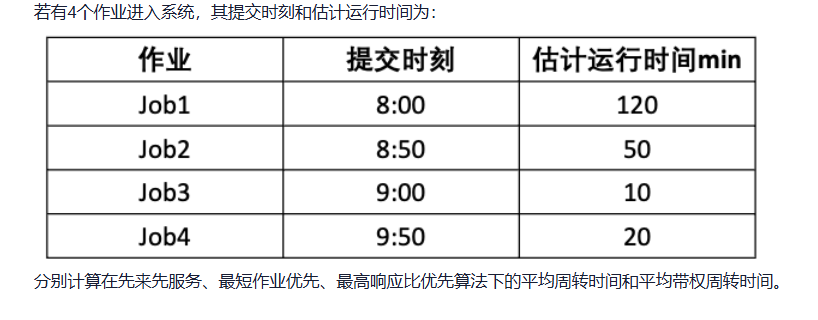
课后第一，二次作业

考虑表1中的候选3-项集，假设hash函数为h(x)=x mod 4，叶节点最大尺寸为2，构造hash树。

表1. 候选3-项集

编号	项集
1	{1, 4, 5}
2	{1, 5, 9}
3	{3, 5, 6}
4	{1, 2, 4}
5	{1, 3, 6}
6	{3, 5, 7}
7	{4, 5, 7}
8	{2, 3, 4}
9	{6, 8, 9}
10	{1, 2, 5}
11	{5, 6, 7}
12	{3, 6, 7}
13	{4, 5, 8}
14	{3, 4, 5}
15	{3, 6, 8}

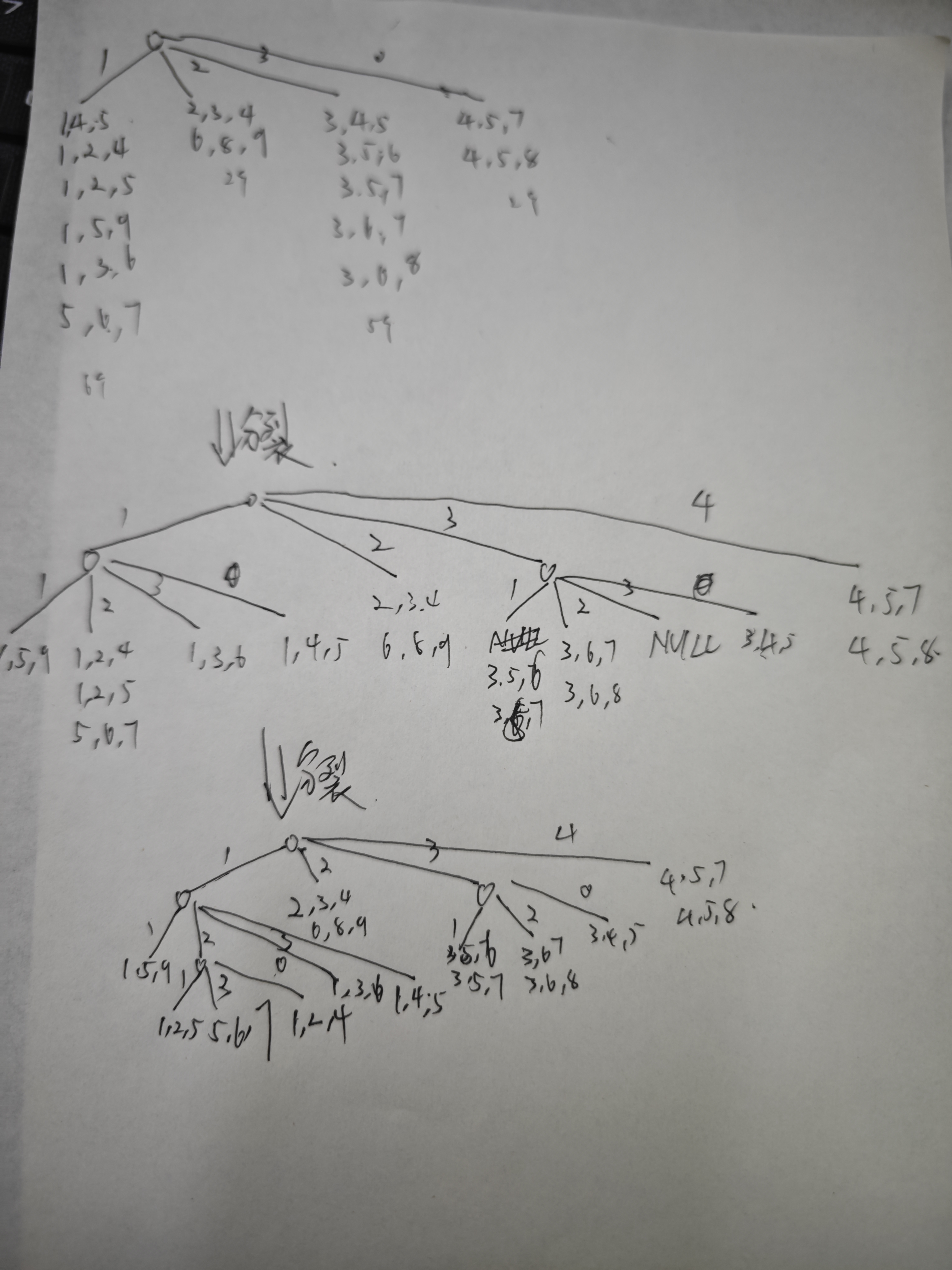
事务集如表2所示，最小支持度阈值是30%。

根据表2的事务集，在格结构上对每个结点添加所有符合条件的字母标记：

N：如果该项集被Apriori算法认为不是候选项集。（一个项集不是候选项集有两种可能的原因，一个是它们没有在候选项集产生步骤产生，另一个是它虽然在候选项集产生步骤产生，但是在剪枝步骤被丢掉）

I：如果计算支持度计数后，该候选项集被认为是非频繁的。

表2. 事务集：

TID	项集
1	{a, b, d, e}
2	{b, c, d}
3	{a, b, d, e}
4	{a, c, d, e}
5	{b, c, d, e}
6	{b, d, e}
7	{c, d}
8	{a, b, c}
9	{a, d, e}
10	{b, d}

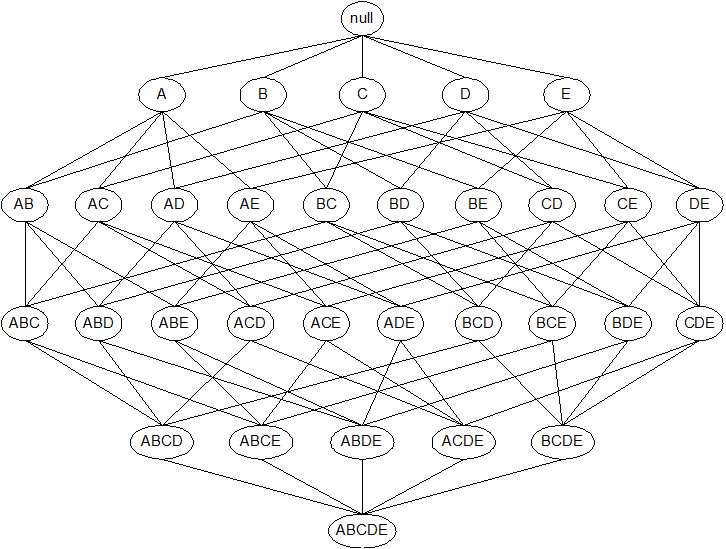
判断极大频繁项集（M）

极大频繁项集：是频繁的，且没有频繁的真超集。

定义：极大频繁项集（Maximal Frequent Itemset）是一个频繁项集，其所有超集都不是频繁的。

检查每个频繁项集：

ade：超集有 abde, acde, adde（无效）, bcde 等，但所有 4-项集都不频繁 → 所以 ade 是极大
bde：同理，超集如 abde, bcde 都不频繁 → bde 是极大
其他频繁项集（如 ad）：有超集 ade（频繁）→ 所以 ad 不是极大
ab：超集 abd（非频繁），abe（非频繁）→ 但 ab 本身频繁，但有没有频繁超集？没有 → 等等！极大要求：没有频繁的超集。abd 支持度=2（非频繁），abe=2（非频繁）→ 所以 ab 没有频繁超集 → 那 ab 是极大？

判断闭频繁项集（C）

闭项集：一个项集 X 是闭的，如果不存在超集 Y ⊃ X 使得 support(Y) = support(X)。

即：它的支持度严格大于所有超集的支持度（或者没有超集具有相同支持度）。

以单项集为例：

单项集：

a (5)：超集 ad(4), ae(4), ab(3), ade(4) → 所有支持度 <5 → 没有超集支持度=5 → a 是闭
b (7)：超集 bd(6), be(4), ab(3), bde(4) → 都 <7 → b 是闭
c (5)：超集 bc(3), cd(4) → 都 <5 → c 是闭
d (9)：超集 ad(4), bd(6), cd(4), de(6), ade(4), bde(4) → 都 <9 → d 是闭
e (6)：超集 ae(4), be(4), de(6) → 注意：de 支持度=6，等于 e 的支持度！
- e ⊂ de，且 support(e)=support(de)=6 → 所以 e 不是闭

课后第三次作业

假设最小支持度阈值为40%，基于以下事务集写出使用FP-growth挖掘频繁项集的过程。

表1. 事务集

TID	项集
1	{a,b,d,e}
2	{b,c,d}
3	{a,b,d,e}
4	{a,c,d,e}
5	{b,c,d,e}

条件 FP 树（Conditional FP-tree）是 FP-growth 算法在“递归”阶段用来压缩“条件模式基”的一棵小 FP 树。它的构建过程与初始 FP 树几乎一样，只是输入数据换成了“条件模式基”，并且再扫一遍、删低计数、排序、插入即可。下面用 “以 e 为后缀” 的例子把每一步都写出来，你就能完全复现。

一、准备：条件模式基（Conditional Pattern Base）

从主 FP 树里提取所有以 e 结尾的路径，并记录该路径的出现次数：

路径（删去 e 本身）	该路径计数
d b a	2
d a c	1
d b c	1

这就是“e 的条件模式基”。

二、第一次扫描：算单项计数

把上面 3 条记录拆成单项累加：

d: 2+1+1 = 4
b: 2+0+1 = 3
a: 2+1+0 = 3
c: 0+1+1 = 2

最小支持度计数仍是 2，因此全部保留（若某项 <2 则直接丢弃）。

三、第二次扫描：排序 + 插入

排序规则：按全局频繁 1-项集的降序排（即 d≻b≻a≻c≻e）。因此每条记录内部重新排序：

原路径	排序后路径	计数
d b a	d b a	2
d a c	d a c	1
d b c	d b c	1

逐条插入，构建“e 的条件 FP 树”：

插入 d b a（计数 2）根 → d(2) → b(2) → a(2)
插入 d a c（计数 1）根 → d(3) → a(1) → c(1)
插入 d b c（计数 1）根 → d(4) → b(3) → c(1)

最终得到的条件 FP 树文字表示：

null
└── d(4)
    ├── b(3)
    │   ├── a(2)
    │   └── c(1)
    └── a(1)
        └── c(1)

linux作业

发表于 2025-09-18 更新于 2025-09-30 分类于大三上，操作系统

用户和权限管理

创建四个系统用户

为系统添加以下四个用户：

alice
bob
john
mike

1
2
3

useradd -d /home/bob -m bob
useradd -d /home/john -m john
useradd -d /home/mike -m mike

为四个用户设置密码

passwd alice
passwd bob
passwd john
passwd mike

创建共享目录

在 /home 目录下创建一个名为 work 的共享目录：

1	mkdir /home/work

创建用户组并添加成员

创建一个名为 workgroup 的用户组：

1	groupadd workgroup

将用户 alice, bob, john 加入该组：

usermod -a -G workgroup alice   # 添加为附加组
usermod -g workgroup alice       # 设置为 alice 的主组（primary group）
usermod -a -G workgroup bob
usermod -a -G workgroup john

主组（Primary Group）：每个用户有且只有一个，是用户创建文件时默认继承的组。
附加组（Supplementary Group）：用户可以有多个，用于额外获得某些组的权限，但不会影响新建文件的默认组。

查看某个组（group）的信息

1	getent group workgroup

修改共享目录的所有权

将 /home/work 目录的属主改为 alice，属组改为 workgroup：

1	chown alice:workgroup /home/work

修改 work 目录的权限

属组内的用户（workgroup 组成员）→ 完全访问权限（rwx）
属组外的用户 → 没有访问权限（—）

1	chmod ug+rwx,o-rwx /home/work

ug+rwx：用户（user）和组（group）都加上读、写、执行权限
o-rwx：其他人（others）去掉所有权限（读、写、执行）

尝试以 bob 用户身份在 work 目录下创建文件

切换到 bob 用户：

su - bob

创建文件：

1	touch /home/work/bob.txt

查看是否成功：

1	ls -l /home/work/bob.txt

尝试以 john 的身份查看或修改 bob.txt

su - john
cat /home/work/bob.txt  #查看文件内容
echo "hello" >> /home/work/bob.txt
ls -l /home/work/bob.txt   #查看权限

尝试以 mike 的身份查看或修改 bob.txt

su - mike
cat /home/work/bob.txt
echo "mike tried" >> /home/work/bob.txt
cd /home/work

进程管理与调试

编写 `badproc.sh` 脚本

Shell 程序（Shell Script） 就是一系列 Shell 命令的集合，写在一个文件里，可以像程序一样自动、批量、重复执行。

#!/bin/bash
while echo "I'm making files!"
do
    mkdir adir
    cd adir
    touch afile
    sleep 10s
done

#!/bin/bash → 指定用 bash 解释器执行

while echo "..." → 无限循环，每次循环前先打印一句话（等价于 while true; do ... done）

循环体内：

创建目录 adir
进入该目录
创建文件 afile
睡眠 10 秒 → 避免太快占满磁盘

添加可执行权限

1
2
3

chmod +x badproc.sh
#验证
ls -l badproc.sh

在后台运行脚本

1	./badproc.sh &

查看进程号

1	ps aux \| grep badproc

杀死进程

1	kill 12345

删除脚本运行时创建的目录和文件

1	rm -rf adir

创建源文件 `fork.c`

#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <sys/types.h>

int main() {
    pid_t pid;

    /* fork another process */
    pid = fork();
    if (pid < 0) { /* error occurred */
        fprintf(stderr, "Fork Failed\n");
        exit(-1);
    }
    else if (pid == 0) { /* child process */
        printf("This is child process, pid=%d\n", getpid());
        execl("/bin/ls", "ls", NULL);  // 执行 ls 命令
        printf("Child process finished\n"); // 这句不会打印，除非 execl 失败
    }
    else { /* parent process */
        printf("This is parent process, pid=%d\n", getpid());
        wait(NULL);  // 等待子进程结束
        printf("Child Complete\n");
        exit(0);
    }
}

编译程序（带调试信息）

1	gcc -g -o fork fork.c

先运行一次，看看效果

./fork

用 `gdb` 调试 fork 程序

gdb ./fork
#在 fork() 调用前设置
(gdb) set follow-fork-mode child
#设置断点和 catch exec
break main
catch exec

Linux编程环境熟悉

C++编译

创建一个名为 helloworld.cpp 的文件，nano helloworld.cpp

#include <iostream>
using namespace std;

int main(void)
{
    cout << "Hello world" << endl;
    return 0;
}

按 Ctrl+O 保存，再按 Ctrl+X 退出 nano

#编译程序
g++ -o hello helloworld.cpp
#运行程序
./hello

创建小型函数库

创建源文件 fred.c 和 bill.c

/* fred.c */
#include <stdio.h>

void fred(int arg)
{
    printf("fred: we passed %d\n", arg);
}

/* bill.c */
#include <stdio.h>

void bill(char *arg)
{
    printf("bill: we passed %s\n", arg);
}

编译成目标文件（.o）

1	gcc -c bill.c fred.c

创建头文件 lib.h

1
2
3

/* lib.h */
void bill(char *);
void fred(int);

创建主程序 program.c

/* program.c */
#include <stdlib.h>
#include "lib.h"   // 引入我们自己写的头文件

int main()
{
    bill("Hello World");
    exit(0);       // 正常退出
}

编译主程序（只编译，不链接）

1	gcc -c program.c

创建静态库 libfoo.a

使用 ar 命令把 bill.o 和 fred.o 打包成一个静态库：

ar：archive 工具，用于创建静态库
c：创建新库
r：将文件插入到库中（如果不存在则添加）
v：显示详细信息

1	ar crv libfoo.a bill.o fred.o

链接主程序和静态库

现在我们要把 program.o 和 libfoo.a 链接起来，生成最终可执行文件 program。

1	gcc -o program program.o libfoo.a

运行程序

./program

操作系统作业

发表于 2025-09-18 更新于 2026-01-05 分类于大三上，操作系统

作业一

1

题目：

在某个计算机系统中有一台输入机和一台打印机，现有两道程序投入运行，且程序A先运行，程序B后开始运行。

程序A的运行轨迹为：
计算50ms，打印100ms，再计算50ms，打印100ms。
程序B的运行轨迹为：
计算50ms，输入80ms，再计算100ms，结束。

问题：

两道程序运行时，CPU是否空闲等待？____（有空闲等待 / 无空闲等待）
若有，在哪段时间内等待？_ms - _ms（两个空，第一个填起始时间，第二个填结束时间，仅数字）
程序A，B是否有等待CPU的情况？
A：（有等待 / 无等待）
B：（有等待 / 无等待）
若有，指出发生等待的时刻（若无等待，空格填0）
（若有两段以上等待时间，用“/”标表示不同等待时间，如0/30和20/40表示0ms-20ms是第一段空闲；30ms-40ms是第二段空闲）
A：_ms - _ms
B：___ms - ___ms

2

题目：

在单CPU和两台I/O设备（I1和I2）的多道程序设计环境下，同时投入三个作业运行，其执行轨迹如下：

Job1：I2（30ms），CPU（10ms），I1（30ms），CPU（10ms）
Job2：I1（20ms），CPU（20ms），I2（40ms）
Job3：CPU（30ms），I1（20ms）

已知条件：

CPU、I1、I2可以并行工作；
优先级从高到低依次为：Job1、Job2、Job3；
优先级高的作业可以抢占优先级低的作业（抢占式调度）；
所有作业同时投入运行。

问题：

每个作业从投入到完成分别所需的时间。
- Job1：____ ms
- Job2：____ ms
- Job3：____ ms
从作业投入到完成，CPU的利用率是：
- ____ / ____ = ____%（保留小数点后两位）
I/O设备利用率：
- I1 利用率：____ / ____ = ____%（保留小数点后两位）
- I2 利用率：____ / ____ = ____%（保留小数点后两位）

3

题目：

在单机系统中，有同时到达的两个程序A、B，若每个程序单独运行，则使用CPU，DEV1（设备1）、DEV2（设备2）的顺序和时间如下表所示。

运行情况	程序A	程序B
CPU	25	20
DEV1	39	50
CPU	20	20
DEV2	20	20
CPU	20	10
DEV1	30	20
CPU	20	45

给定条件：

DEV1和DEV2是不同的I/O设备，它们能够同时工作。
程序B优先级高于程序A，非抢占式。当程序A占用CPU时，即使程序B需要使用CPU，也不能打断程序A的执行，而应等待。
当使用CPU之后控制转向I/O设备，或者使用I/O设备之后控制转向CPU，由控制程序执行中断处理，但这段处理时间可以忽略不计。

问题：

哪个程序先结束？（A / B）
程序全部执行结束需要多少时间？（____ ms）
程序全部执行完毕时，CPU利用率是多少？（____%）
A程序等待CPU的累积时间是多少？（____ ms）
B程序等待CPU的累积时间是多少？（____ ms）

作业二

1

2

3

作业三

1

有一个盒子里混装了数量相等的黑白围棋子，现在利用自动分拣系统把黑子、白子分开，设分拣系统有两个进程P1和P2，其中进程P1拣白子，进程P2拣黑子。规定每个进程每次拣一子；当一个进程在拣时，不允许另一个进程去拣；当一个进程拣了一子时，必须让另一个进程去拣。试写出进程P1和P2能够正确并发执行的程序。

2

请用信号量和PV操作解决以下问题：桌上有一只盘子，最多可以容纳两个水果，每次仅能放入或取出一个水果。爸爸专向盘子中放苹果(apple)，妈妈专向盘子中放橘子(orange)，两个儿子专等吃盘子中的桔子，两个女儿专等吃盘子里的苹果。写出爸爸（father）、妈妈（mother）、儿子（son）和女儿（daughter）进程及所需定义的变量和信号量。用PV操作实现爸爸、妈妈、儿子、女儿间的同步与互斥关系。

3

设当前的系统状态如下，此时Available=(1,1,2)

进程	Claim (R1, R2, R3)	Allocation (R1, R2, R3)	Available (R1, R2, R3)
P1	3, 2, 2	1, 0, 0	1, 1, 2
P2	6, 1, 3	5, 1, 1
P3	3, 1, 4	2, 1, 1
P4	4, 2, 2	0, 0, 2

作业四

1

数组int A[100][100]；元素按行存储，在虚拟系统中，采用LRU淘汰算法，一个进程有3页内存空间，每页可以存放200个整数，其中第1页存放程序，假定程序已在内容中，问：

A程序缺页次数为：____次；

B程序缺页次数为：____次。

程序A：

for(int i=0; i<100; i++)
   for(int j=0; j<100; j++)
        A[i,j]=0;

程序B：

for(int j=0;j<100;j++)
   for(int i=0;i<100;i++)   
        A[i,j]=0;

程序 A 分析

代码逻辑：

1
2
3

for(int i=0; i<100; i++)    // 外层循环：行
   for(int j=0; j<100; j++) // 内层循环：列
      A[i][j]=0;

访问顺序：A[0][0], A0, …, A[0][99], A[1][0], …

这是按行访问，与数组的按行存储顺序一致。

缺页计算过程：

访问第0、1行：都在虚拟页0中。
- 第一次访问 A[0][0] 时，内存为空，发生 1次缺页，调入页0。
- 后续访问第0行和第1行的剩余199个元素时，都在页0中，直接命中（不缺页）。
访问第2、3行：都在虚拟页1中。
- 访问 A[2][0] 时，页1不在内存，发生 1次缺页，调入页1。
- 后续元素全部命中。
以此类推：
- 程序按照顺序访问：页0 → 页1 → 页2 … → 页49。
- 由于我们有2个物理块，LRU算法会淘汰最久未使用的旧页面，但因为访问是单向顺序向前的，每一页只需要调入一次。

结果：共有50个页面，每页调入一次。

Total = 50 次缺页。

程序 B 分析

代码逻辑：

1
2
3

for(int j=0; j<100; j++)    // 外层循环：列
   for(int i=0; i<100; i++) // 内层循环：行
      A[i][j]=0;

访问顺序：A[0][0], A[1][0], A[2][0], …

这是按列访问，即“跳跃式”访问。

缺页计算过程：

分析内层循环（i 从 0 到 99，处理第 j 列）：
- i=0, 1: 访问第0、1行 → 需要 虚拟页0。
- i=2, 3: 访问第2、3行 → 需要 虚拟页1。
- …
- i=98, 99: 访问第98、99行 → 需要 虚拟页49。
- 一轮内循环（i=0~99）会依次访问：页0, 页1, 页2, …, 页49。
内存状态与置换：
- 我们只有 2个物理块用于数据。
- 当访问页0、页1时，填满内存。
- 当需要页2时，根据LRU，淘汰页0。
- 当需要页3时，根据LRU，淘汰页1。
- …
- 因为循环访问的页面数量（50页）远大于物理内存（2页），导致内存中的页面不断被替换（颠簸/Thrashing现象）。
- 结论：在处理每一列（内层循环）时，需要访问所有50个页面。因为内存存不下，这 50个页面每一次都需要重新从磁盘调入。
- 单列（一次外层循环）产生的缺页次数 = 50次。
结合外层循环：
- 外层循环 j 从 0 到 99，共执行 100次。
- 每次外层循环都要重新把这50个页面遍历一遍。由于上一轮留下的页面（最后访问的页48、49）对下一轮开头需要的页（页0）没有帮助。
- 总缺页次数 = 每列缺页数 × 列数
- Total = 50 × 100 = 5000。

结果：5000 次缺页。

2

在一个请求分页虚存管理系统中，一个程序运行的页面走向是：1 2 3 4 2 1 5 6 2 1 2 3 7 6 3 2 1 2 3 6

分别用FIFO、OPT、和LRU算法，对于分配给程序3个页框的情况，求出缺页异常次数和缺页中断率：

（1）FIFO：缺页异常次数：_____次, 缺页中断率：______%.

（2）OPT：缺页异常次数：_____次, 缺页中断率：______%.

（3）LRU：缺页异常次数：_____次, 缺页中断率：______%.

3

一个页式虚拟存储管理系统中的用户空间为1024KB，页面大小为4KB，内存空间为512KB。已知用户的10、11、12、13号虚页分得的内存页框号为62、78、25、36，试将逻辑地址0BEBCH转换为对应的物理地址: _______H。

名词	英文	所在空间	本质	通俗解释（类比）
页面 (Page)	Page	逻辑/虚拟空间 (程序里)	程序被切分成的“块”	客人 (要住店的人)
页号 (Page No.)	VPN	逻辑/虚拟空间	页面的编号/索引	客人的身份证号
页框 (Page Frame)	Page Frame	物理内存 (硬件里)	内存条被切分成的“格”	酒店的房间 (物理存在的空间)
页块 (Block)	Physical Block	物理内存	完全等同于“页框” (别名)	完全等同于“房间”
页框号 (PFN)	PFN	物理内存	页框的物理编号	房间号码 (如 302 号房)
页表 (Page Table)	Page Table	内存中 (系统管理)	映射表 (记录对应关系)	前台登记簿 (记录谁住哪个房间)

作业五

matlab与opencv基本操作

发表于 2025-09-15 更新于 2025-11-12 分类于大三上，数字图像处理

前言

本文讲解matlab~~与opencv~~对图像处理的基础操作，代码会有matlab~~与python两版~~，可对比学习。

读写

读入图像

matlab

1	I = imread('cameraman.jpg');

python

1	I = cv2.imread('cameraman.jpg', cv2.IMREAD_COLOR)

cv2.IMREAD_COLOR = 强制读成 3 通道 BGR 彩色图。

存入图像

matlab

1	imwrite(J,'cameramanC.jpg');

python

1	cv2.imwrite('cameramanC.jpg', J)

读图并转 double

matlab

1	Image1 = im2double(imread('lotus.jpg'));

imread 把图像读成 0-255 的 uint8。
im2double 把像素值线性缩放到 0–1 浮点，方便后续计算。

为什么要转成double

如果像素是 0–255，你在代码里写 0.299*r 就永远只用到 0.299×255≈76 灰度级，结果会整体偏暗甚至直接截断。

几级灰度的含义是什么

几级灰度”这句话里的“级”就是“台阶”的意思：把黑→白这段连续亮度等间隔切成多少份，就有多少个离散台阶，叫多少灰度级。

2 级灰度 → 纯黑 + 纯白，一共 2 个台阶（1 bit）

8 级灰度 → 0, 36, 73, 109, 146, 182, 219, 255（3 bit）

256 级灰度 → 0–255，共 256 个台阶（8 bit）

uint8 是“Unsigned Integer, 8 bit”的缩写，含义一句话：

无符号、8 位、整型数字，只能放 0–255 的整数。

图像操作

反色

J=255-I;

提取通道

matlab

1
2
3

r = Image1(:,:,1);
g = Image1(:,:,2);
b = Image1(:,:,3);

分别提取rgb三个通道

opencv

1 2	matlab:g = Image1(1,1,2)提取G通道的第一个像素点 opencv:g = image[0,0,1]

opencv是从下标0开始

合并通道

NTSC 标准

1	Y = 0.299r + 0.587g + 0.114*b;

0.299、0.587、0.114 是 NTSC 在 1953 年定下的“亮度加权系数”，源于人眼三种视锥细胞对 R、G、B 光谱的灵敏度——绿最亮、红次之、蓝最暗

二值化（阈值 0.3）

1 2	BW = zeros(size(Y)); % 先全黑 BW(Y > 0.3) = 1; % 亮度>0.3 的像素置 1（白）

从RGB颜色空间转换成HSI颜色空间

matlab

1	hsi = rgb2hsv(img);

HSI 颜色空间是把一幅彩色图像的每个像素拆成 3 个独立、且更符合人眼感知习惯的物理量：

H（Hue，色调）用 0°–360° 的“角度”表示“到底是什么颜色”。例：0°≈红，120°≈绿，240°≈蓝，绕一圈回到红。
S（Saturation，饱和度） 0–1（或 0–100%）表示“颜色有多鲜艳”。 0 → 灰，1 → 最纯、最艳。
I（Intensity，亮度/强度） 0–1（或 0–255）表示“有多亮”，与颜色本身无关，只反映明暗。

RGB 是“机器友好”的立方体坐标，但人眼很难从 (R,G,B) 直接说出“颜色、多艳、多亮”。

matlab基本操作

获取图像行列和通道数

1	[N,M,~]=size(r);

把二维矩阵 r 的“行数”赋给 N，“列数”赋给 M。

截取图像

1	newimage=img(H/4:H3/4,W/4:W3/4,:);

人脸肤色检测

YCrCb 阈值法

Y “Luma”——亮度（Luminance）。对应人眼最敏感的黑↔︎白信息，决定了你看到的“明暗”。计算公式近似：
1
Y = 0.299·R + 0.587·G + 0.114·B
Cr “Chroma-red”——红色色度。表示 红色与亮度的差值：Cr = R – Y
Cb “Chroma-blue”——蓝色色度。表示 蓝色与亮度的差值：Cb = B – Y

人眼对 绿色最敏感，对 红、蓝最迟钝。把“绿色”信息扔掉，只保留 R-Y 和 B-Y 两个差值，就能 最小化数据量，同时 还能把颜色还原回来。

人类肤色在 YCrCb 颜色空间呈明显的“聚类”特性：无论人种如何，Cb、Cr 两个色度分量都落在狭长带状区域。
选取经验区间（Cr ∈ [133,173]，Cb ∈ [77,127]）直接做 2D 门限，亮度 Y 不参与判断，因此对光照强度变化不敏感，但对色偏敏感。

def skin_YCrCb(img):
    #把一张 BGR 彩色图像从“蓝-绿-红”颜色空间转换到“亮度-红度-蓝度”颜色空间（YCrCb）
    ycrcb = cv2.cvtColor(img, cv2.COLOR_BGR2YCrCb)
    min_YCrCb = np.array([0, 133, 77])
    max_YCrCb = np.array([255, 173, 127])
    '''
把落在 [min_YCrCb, max_YCrCb] 立方体内的像素标为 255（白），其余标为 0（黑），返回一张单通道掩膜图。
执行过程（逐像素）：
取 ycrcb 的一个像素 (y, cr, cb)
检查是否同时满足
min_Y ≤ y ≤ max_Y
min_Cr ≤ cr ≤ max_Cr
min_Cb ≤ cb ≤ max_Cb
满足 → 输出 255；任一通道不满足 → 输出 0
    '''
    skin = cv2.inRange(ycrcb, min_YCrCb, max_YCrCb)
    return skin

HSV 阈值法

肤色聚类现象大量统计表明：

不同人种、不同光照 的肤色在 RGB 空间里沿对角线“灰度轴”散开 → 亮度影响大。
转到 HSV 后，Hue 坐标紧紧挤在 0-20° 之间（红-橙-黄），S 中等偏高，V 中等偏亮

def skin_HSV(img):
    hsv = cv2.cvtColor(img, cv2.COLOR_BGR2HSV)
    low  = np.array([0,  30,  60])
    high = np.array([20, 150, 255])
    skin = cv2.inRange(hsv, low, high)
    return skin

椭圆模型法

原理：将RGB图像转换到YCRCB空间，肤色像素点会聚集到一个椭圆区域。先定义一个椭圆模型，然后将每个RGB像素点转换到YCRCB空间比对是否再椭圆区域，是的话判断为皮肤。

# ---------------- 3. 椭圆模型法 ----------------
def skin_ellipse(img):
    ycrcb = cv2.cvtColor(img, cv2.COLOR_BGR2YCrCb)
    # 如果本地没有模型图，现场画一张 256×256 查找表
    ellipse_model = cv2.imread('ellipse_skin_model.png', 0)
    if ellipse_model is None:
        ellipse_model = np.zeros((256, 256), dtype=np.uint8)
        cv2.ellipse(ellipse_model, (113, 155), (23, 15),
                    43, 0, 360, 255, -1)
    cr = ycrcb[:, :, 1].astype(np.uint16)  # 防止溢出
    cb = ycrcb[:, :, 2].astype(np.uint16)
    indices = cr * 256 + cb
    skin = np.take(ellipse_model, indices)
    return skin

将彩色图像 Image1 的 R、B 通道互换

1	img_swap = img(:,:,[3 1 2]);

在 MATLAB 中，读取彩色图像（如用 imread）默认是 RGB 顺序：

第1通道：Red（红）
第2通道：Green（绿）
第3通道：Blue（蓝）

但在 OpenCV（Python/C++） 中，图像默认是 BGR 顺序：

第1通道：Blue
第2通道：Green
第3通道：Red

使用或操作，进行图像的嵌入

clear; clc; close all;  % 清空所有变量
% 读取两张图片
background = imread('图片2.png');   
butterfly = imread('图片1.png');  

% 设置缩放比例
scale = 0.5;
small_butterfly = imresize(butterfly, scale, 'bilinear');

% 获取尺寸
[ih, iw, ~] = size(small_butterfly);
x = 200; y = 400;

% 提取背景中对应区域
bg_patch = background(x:x+ih-1, y:y+iw-1, :);

is_black = any(small_butterfly~=0,3);   % 蝴蝶主体区域

%只把背景中“蝴蝶主体对应位置”设为 0
% 获取尺寸
[ih, iw, ~] = size(bg_patch);

% 双重循环遍历每个像素
for i = 1:ih
    for j = 1:iw
        if is_black(i, j)   % 如果该位置是蝴蝶主体（非黑）
            bg_patch(i, j, 1) = 0;  % R 通道设为 0
            bg_patch(i, j, 2) = 0;  % G 通道设为 0
            bg_patch(i, j, 3) = 0;  % B 通道设为 0
        end
    end
end

%现在做 bitor：0 | butterfly = butterfly，背景黑区 | 0 = 背景
patch_bitor = bitor(bg_patch, small_butterfly);

% 写回背景
background(x:x+ih-1, y:y+iw-1, :) = patch_bitor;

% 显示结果
figure;
subplot(1,3,1), imshow(small_butterfly), title(['缩小后的蝴蝶 (', num2str(scale*100), '%)']);
subplot(1,3,2), imshow(bg_patch), title('处理后的背景块（蝴蝶位置清黑）');
subplot(1,3,3), imshow(background), title('最终合成图（bitor）');

利用单尺度和多尺度 Retinex 增强方法实现图像增强

I = imread('gugong1.jpg');

if ndims(I) == 3
    I_gray = rgb2gray(I);
else
    I_gray = I;
end

I_double = double(I_gray) + eps;

% SSR
sigma = 15;
L_ssr = log(conv2(I_double, fspecial('gaussian', [31, 31], sigma), 'same'));
R_ssr = log(I_double) - L_ssr;
ssr_img = mat2gray(R_ssr);

% MSR
sigmas = [15, 80, 250];
weights = [0.33, 0.34, 0.33];
R_msr = zeros(size(I_double));
for k = 1:length(sigmas)
    sigma = sigmas(k);
    kernel_size = round(6 * sigma) + 1;
    if mod(kernel_size, 2) == 0
        kernel_size = kernel_size + 1;
    end
    L = log(conv2(I_double, fspecial('gaussian', [kernel_size, kernel_size], sigma), 'same'));
    R_msr = R_msr + weights(k) * (log(I_double) - L);
end
msr_img = mat2gray(R_msr);

figure;
subplot(1,3,1); imshow(I); title('Original');
subplot(1,3,2); imshow(ssr_img); title('SSR');
subplot(1,3,3); imshow(msr_img); title('MSR');

直方图均衡化计算

5.4代码

opencv

import numpy as np
import matplotlib.pyplot as plt

# --- Step 1: 构造原始图像 ---
gray_levels = np.array([0, 1/7, 2/7, 3/7, 4/7, 5/7, 6/7, 1])  # 原始灰度值 (0~1)
pixel_counts = np.array([560, 920, 1046, 705, 356, 267, 170, 72])
total_pixels = 64 * 64  # 4096

# 将灰度值映射到整数 0~7 用于图像存储
int_gray_levels = np.round(gray_levels * 7).astype(int)  # [0,1,2,3,4,5,6,7]

# 创建图像数组
img = np.zeros(total_pixels, dtype=np.uint8)

start_idx = 0
for i, count in enumerate(pixel_counts):
    img[start_idx:start_idx + count] = int_gray_levels[i]
    start_idx += count

img = img.reshape((64, 64))  # 重塑为 64x64 图像

# --- Step 2: 直方图均衡化 ---
hist, _ = np.histogram(img, bins=8, range=(0, 8))
cdf = np.cumsum(hist) / total_pixels
mapping = np.round(cdf * 7).astype(int)
equalized_img = mapping[img]

# --- Step 3: 可视化对比 ---
plt.figure(figsize=(8, 4))

plt.subplot(1, 2, 1)
plt.imshow(img, cmap='gray', vmin=0, vmax=7)
plt.title('Original')
plt.axis('off')

plt.subplot(1, 2, 2)
plt.imshow(equalized_img, cmap='gray', vmin=0, vmax=7)
plt.title('Equalized')
plt.axis('off')

plt.tight_layout()
plt.show()

landingpage调研

发表于 2025-09-14 更新于 2025-09-15 分类于实习， Tosea.ai

landingpage的组成

1.开始界面，大概说明产品的定位和作用，让用户可以快速注册后进入

Grammarly: Free AI Writing Assistance

2.展示产品的特点功能和使用范例：1.特点功能这块可以像manus把使用过程中比较有特点的功能截屏，做成下面这样；2.范例部分结构可以参考manus或者lovart垂直滑动的效果，效果可以参考genspackGenspark - AI 幻灯片

专为演示文稿打造的 Gamma | 利用 AI 立即构建演示文稿 | Gamma

3.用户的声音，价格。用户声音我觉得参考lovart就可以，声音这边也可以使用一个滚动的效果

TRAE - Collaborate with Intelligence

我感觉我们的风格应该还是要简约大气

PPtYoda技术调用

这个项目的核心就是基于python-pptx的这个包，其实跟我们不是很符合。

他们ppt生成的逻辑核心是模板，一定要有pptx模板，并带有每个部分的备注，上传后解析，把ppt的各个结构转化成json存储

file = models.FileField(
        upload_to=get_template_path,
        storage=ppt_storage,
    )
    created_at = models.DateTimeField(auto_now_add=True)

    cover_template = models.JSONField(null=True, blank=True, default=dict)
    toc_template = models.JSONField(null=True, blank=True, default=dict)
    chapter_L1_template = models.JSONField(null=True, blank=True, default=dict)
    chapter_L2_template = models.JSONField(null=True, blank=True, default=dict)
    blank_template = models.JSONField(null=True, blank=True, default=dict)

    slide_templates = models.JSONField(null=True, blank=True, default=list)
    components = models.JSONField(null=True, blank=True, default=list)
    sections = models.JSONField(null=True, blank=True, default=dict)

生成ppt时，也是让大模型生成符合这种规范的json，然后通过python-pptx填入。

这样好处确实是解决了使用python-pptx时，生成的ppt结构混乱的问题，但是这样生成的ppt完全依赖于你输入的模板，灵活性上有所缺陷。

后续任务

1.导出speaknotes-pdf后端

2.生成完整presentation

postgresql

发表于 2025-09-11 更新于 2025-11-07 分类于 python-web ， postgresql

docker部署

docker pull postgres

docker run -d --name pgsql \
  -p 5432:5432 \
  -e POSTGRES_PASSWORD=123456 \
  -v D:\database\postgresql:/var/lib/postgresql/data \
  postgres
  
  docker run -d --name pgsql -p 5432:5432 -e POSTGRES_PASSWORD=123456 -v D:\database\postgresql:/var/lib/postgresql/data postgres

docker 运行postgresql 极限简洁教程 - 刘老六 - 博客园

恢复数据库

使用pg_restore

# 1. 删除现有数据库
psql -U postgres -c "DROP DATABASE dvdrental;"

# 2. 重建空数据库
psql -U postgres -c "CREATE DATABASE dvdrental;"

pg_restore --dbname=postgresql://postgres:123456@localhost:5432/dvdrental --no-owner /workspace/dvdrental

以下是数据库导入的原理

作用：Table of Contents，包含备份的元数据信息

内容：数据库结构、表定义、索引、约束、函数等的描述

格式：二进制格式，记录了所有数据库对象的信息

数据文件（3038.dat, 3040.dat, …）

作用：存储实际的表数据

命名规则：数字对应数据库对象的 OID（Object Identifier）

restore.sql（可选的SQL脚本）

作用：包含恢复数据库的 SQL 命令

内容：CREATE TABLE、INSERT、索引创建等语句

pg_restore 工作流程

读取 toc.dat
创建数据库结构
创建约束和索引

SQLAlchemy ORM

范例

---
config:
  layout: elk
---
erDiagram
    零件（Part） ||--o{ 库存（Inventory） : "存放"
    库房（Warehouse） ||--o{ 库存（Inventory） : "包含"
    供应商（Supplier） ||--o{ 采购（Purchase） : "供应"
    零件（Part） ||--o{ 采购（Purchase） : "被采购"
    库房（Warehouse） ||--o{ 采购（Purchase） : "接收"
    库房（Warehouse） }|--|| 职工（Staff） : "组长"
    库房（Warehouse） ||--o{ 职工（Staff） : "雇佣"
    零件（Part） {
        string part_id PK "零件编号"
        string name "名称"
        decimal unit_price "单价"
        string type "类型"
    }
    供应商（Supplier） {
        string supplier_id PK "供应商编号"
        string name "名称"
        string address "地址"
        string phone "电话"
    }
    库房（Warehouse） {
        string warehouse_id PK "库房号"
        string address "地址"
    }
    职工（Staff） {
        string staff_id PK "职工号"
        string name "姓名"
        string gender "性别"
        date hire_date "进厂时间"
        string title "职称"
        string warehouse_id FK "所属库房"
    }
    库存（Inventory） {
        string warehouse_id PK,FK "库房号"
        string part_id PK,FK "零件编号"
        int stock_quantity "库存数量"
    }
    采购（Purchase） {
        string purchase_id PK "采购单号"
        string part_id FK "零件编号"
        string supplier_id FK "供应商编号"
        string warehouse_id FK "库房号"
        date purchase_date "采购日期"
        int quantity "进货数量"
        decimal actual_price "实际单价"
    }

# models.py
from sqlalchemy import (
    create_engine, Column, String, Integer, DECIMAL, Date, CHAR,
    ForeignKey, CheckConstraint, UniqueConstraint
)
from sqlalchemy.ext.declarative import declarative_base
from sqlalchemy.orm import relationship

# SQLAlchemy 的基类，所有模型类都需要继承这个 Base
# declarative_base() 创建了一个基类，用于定义数据库表结构的映射
Base = declarative_base()

class Part(Base):
    __tablename__ = 'part'
    
    part_id = Column(String(20), primary_key=True)
    name = Column(String(100), nullable=False)
    unit_price = Column(DECIMAL(10, 2), nullable=False)
    type = Column(String(50), nullable=False)
    
    # 约束：单价 >= 0
    __table_args__ = (
        CheckConstraint(unit_price >= 0, name='check_unit_price_positive'),
    )

class Supplier(Base):
    __tablename__ = 'supplier'
    
    supplier_id = Column(String(20), primary_key=True)
    name = Column(String(100), nullable=False)
    address = Column(String(200))
    phone = Column(String(20))

class Warehouse(Base):
    __tablename__ = 'warehouse'
    
    warehouse_id = Column(String(20), primary_key=True)
    address = Column(String(200), nullable=False)

    # 可选：未来加组长时在此添加
    # leader_staff_id = Column(String(20), ForeignKey('staff.staff_id'), unique=True)

class Staff(Base):
    __tablename__ = 'staff'
    
    staff_id = Column(String(20), primary_key=True)
    name = Column(String(50), nullable=False)
    gender = Column(CHAR(1))
    hire_date = Column(Date, nullable=False)
    title = Column(String(50))
    warehouse_id = Column(String(20), ForeignKey('warehouse.warehouse_id'), nullable=False)
    
    # 约束：性别只能是 M/F
    __table_args__ = (
        CheckConstraint("gender IN ('M', 'F')", name='check_gender'),
    )

class Inventory(Base):
    __tablename__ = 'inventory'
    
    warehouse_id = Column(String(20), ForeignKey('warehouse.warehouse_id'), primary_key=True)
    part_id = Column(String(20), ForeignKey('part.part_id'), primary_key=True)
    stock_quantity = Column(Integer, nullable=False)
    
    # 表级约束：确保库存数量不能为负数
    # 当尝试插入或更新为负数时会触发数据库错误
    __table_args__ = (
        CheckConstraint(stock_quantity >= 0, name='check_stock_non_negative'),
    )

class Purchase(Base):
    __tablename__ = 'purchase'
    
    purchase_id = Column(String(30), primary_key=True)
    part_id = Column(String(20), ForeignKey('part.part_id'), nullable=False)
    supplier_id = Column(String(20), ForeignKey('supplier.supplier_id'), nullable=False)
    warehouse_id = Column(String(20), ForeignKey('warehouse.warehouse_id'), nullable=False)
    purchase_date = Column(Date, nullable=False)
    quantity = Column(Integer, nullable=False)
    actual_price = Column(DECIMAL(10, 2), nullable=False)
    
    # 表级约束：确保采购业务逻辑的合理性
    # - 采购数量必须为正数（不能为零或负数）
    # - 实际采购价格必须为正数（不能为零或负数）
    __table_args__ = (
        CheckConstraint(quantity > 0, name='check_quantity_positive'),
        CheckConstraint(actual_price > 0, name='check_price_positive'),
    )

建立表

1	DATABASE_URL = "postgresql://postgres:123456@localhost:5432/factory_db"

# create_tables.py
from sqlalchemy import create_engine
from models import Base
from dotenv import load_dotenv
import os

load_dotenv()

# 替换为你的 Docker PostgreSQL 地址
DATABASE_URL = os.getenv("DATABASE_URL")

# 创建数据库引擎，用于连接数据库
# create_engine 会根据 DATABASE_URL 创建对应的数据库连接池
engine = create_engine(DATABASE_URL)
Base.metadata.create_all(engine)  # 自动建表！
print("✅ 所有表已创建")

rag增强技术汇总

发表于 2025-09-08 分类于 rag

各类 RAG 增强技术

如何提高 RAG 管道的性能 | Milvus 文档

可以通过此GitHub 链接获得本文所列主要方法的简单实现。

我们可以根据 RAG 管道各阶段的作用对不同的 RAG 增强方法进行分类。

查询增强：修改和操作 RAG 输入的查询过程，以便更好地表达或处理查询意图。
增强索引：使用多分块、分步索引或多向索引等技术优化分块索引的创建。
检索器增强：在检索过程中应用优化技术和策略。
生成器增强：在为 LLM 生成提示时调整和优化提示，以提供更好的响应。
增强 RAG 管道：在整个 RAG 管道中动态切换流程，包括使用 Agents 或工具来优化 RAG 管道中的关键步骤。

接下来，我们将介绍每个类别下的具体方法。

查询增强

共有四种方式：假设问题、假设文档嵌入、子查询和回溯提示。接下来我将选取几个具体说明。

HyDE（假设文档嵌入）

HyDE 是假设文档嵌入的缩写。它利用 LLM 制作一个“假设文档*”或虚假*答案，以回应没有上下文信息的用户查询。然后，这个假答案会被转换成向量嵌入，并用于查询向量数据库中最相关的文档块。随后，向量数据库会检索出 Top-K 最相关的文档块，并将它们传送给 LLM 和原始用户查询，从而生成最终答案。

这种方法在解决向量搜索中的跨域不对称问题方面与假设问题技术类似。不过，它也有缺点，如增加了计算成本和生成虚假答案的不确定性。

创建子查询

当用户查询过于复杂时，我们可以使用 LLM 将其分解为更简单的子查询，然后再将其传递给向量数据库和 LLM。让我们来看一个例子。

想象一下，用户会问*“Milvus 和 Zilliz Cloud 在功能上有什么不同？*”这个问题相当复杂，在我们的知识库中可能没有直接的答案。为了解决这个问题，我们可以将其拆分成两个更简单的子查询：

子查询 1：“Milvus 有哪些功能？”
子查询 2：“Zilliz Cloud 有哪些功能？”

有了这些子查询后，我们将它们全部转换成向量嵌入后发送给向量数据库。然后，向量数据库会找出与每个子查询最相关的 Top-K 文档块。最后，LLM 利用这些信息生成更好的答案。

增强索引

增强索引是提高 RAG 应用程序性能的另一种策略。让我们来探讨三种索引增强技术：自动合并文档块，构建分层索引，混合检索和重新排名

构建分层索引

在创建文档索引时，我们可以建立两级索引：一级是文档摘要索引，另一级是文档块索引。向量搜索过程包括两个阶段：首先，我们根据摘要过滤相关文档，随后，我们在这些相关文档中专门检索相应的文档块。

在涉及大量数据或数据分层的情况下，例如图书馆 Collections 中的内容检索，这种方法证明是有益的。

混合检索和重新排名

混合检索和重排技术将一种或多种辅助检索方法与向量相似性检索相结合。然后，Reranker会根据检索结果与用户查询的相关性对检索结果重新排序。

常见的补充检索算法包括基于词频的方法（如BM25）或利用稀疏嵌入的大模型（如SPLADE）。重新排序算法包括 RRF 或更复杂的模型，如Cross-Encoder（类似于 BERT 的架构）。

改进检索器

改进 RAG 系统中的检索器组件也能改进 RAG 应用。让我们来探讨一些增强检索器的有效方法：句子窗口检索，元数据过滤

生成器增强

让我们通过改进 RAG 系统中的生成器来探索更多 RAG 优化技术：压缩 LLM 提示，调整提示中的块顺序

调整提示中的块顺序

在论文Lost in the Middle“中，研究人员观察到，LLMs 在推理过程中经常会忽略给定文档中间的信息。相反，他们往往更依赖于文档开头和结尾的信息。

根据这一观察结果，我们可以调整检索知识块的顺序来提高答案质量：在检索多个知识块时，将置信度相对较低的知识块放在中间，而将置信度相对较高的知识块放在两端。

增强 RAG 管道

我们还可以通过增强整个 RAG 管道来提高 RAG 应用程序的性能。

自我反思

这种方法在人工智能 Agents 中融入了自我反思的概念。那么，这种技术是如何工作的呢？

一些最初检索到的 Top-K 文档块是模棱两可的，可能无法直接回答用户的问题。在这种情况下，我们可以进行第二轮反思，以验证这些文档块是否能真正解决查询问题。

我们可以使用高效的反思方法（如自然语言推理（NLI）模型）进行反思，也可以使用互联网搜索等其他工具进行验证。

使用代理进行查询路由选择

有时，我们不必使用 RAG 系统来回答简单的问题，因为它可能会导致更多的误解和对误导信息的推断。在这种情况下，我们可以在查询阶段使用代理作为路由器。这个 Agents 会评估查询是否需要通过 RAG 管道。如果需要，则启动后续的 RAG 管道；否则，LLM 直接处理查询。

Agents 可以有多种形式，包括 LLM、小型分类模型，甚至是一组规则。

通过根据用户意图路由查询，可以重新定向部分查询，从而显著提高响应时间，并明显减少不必要的噪音。

我们可以将查询路由技术扩展到 RAG 系统内的其他流程，例如确定何时利用网络搜索等工具、进行子查询或搜索图片。这种方法可确保 RAG 系统中的每个步骤都能根据查询的具体要求进行优化，从而提高信息检索的效率和准确性。

milvus

发表于 2025-09-08 更新于 2025-09-20 分类于 python-web ， milvus

为什么使用milvus

非结构化数据（如文本、图像和音频）格式各异，蕴含丰富的潜在语义，因此分析起来极具挑战性。为了处理这种复杂性，Embeddings 被用来将非结构化数据转换成能够捕捉其基本特征的数字向量。然后将这些向量存储在向量数据库中，从而实现快速、可扩展的搜索和分析。

Milvus 提供强大的数据建模功能，使您能够将非结构化或多模式数据组织成结构化的 Collections。它支持多种数据类型，适用于不同的属性模型，包括常见的数字和字符类型、各种向量类型、数组、集合和 JSON，为您节省了维护多个数据库系统的精力。

部署（windows）

在 Docker（Linux）中运行 Milvus | Milvus 文档

# Download the configuration file and rename it as docker-compose.yml
C:\>Invoke-WebRequest https://github.com/milvus-io/milvus/releases/download/v2.6.0/milvus-standalone-docker-compose.yml -OutFile docker-compose.yml

# Start Milvus
C:\>docker compose up -d

注意设置环境变量DOCKER_VOLUME_DIRECTORY来决定卷映射的路径

容器	镜像	在 Milvus 中的角色	一句话说明
etcd	quay.io/coreos/etcd:v3.5.18	元数据与协调中心	负责“记帐”——存索引结构、集合信息、节点心跳等，相当于 Milvus 的“大脑备忘录”。
minio	minio/minio:RELEASE.2024-12-18T13-15-44Z	对象存储	负责“存文件”——把向量索引文件、大字段、日志快照等落地成对象，相当于 Milvus 的“硬盘”。
standalone	milvusdb/milvus:v2.6.0	计算节点（单机版）	负责“干活”——接受 SDK 请求、做向量检索、构建索引，相当于 Milvus 的“工人”。

安装

1	pip install -U pymilvus

基本概念

数据库

在 Milvus 中，数据库是组织和管理数据的逻辑单元。为了提高数据安全性并实现多租户，你可以创建多个数据库，为不同的应用程序或租户从逻辑上隔离数据。例如，创建一个数据库用于存储用户 A 的数据，另一个数据库用于存储用户 B 的数据。

collections

在 Milvus 上，您可以创建多个 Collections 来管理数据，并将数据作为实体插入到 Collections 中。Collections 和实体类似于关系数据库中的表和记录。

Collection 是一个二维表，具有固定的列和变化的行。每列代表一个字段，每行代表一个实体。

下图显示了一个有 8 列和 6 个实体的 Collection。

schema

Schema 定义了 Collections 的数据结构。在创建一个 Collection 之前，你需要设计出它的 Schema。

设计良好的 Schema 至关重要，因为它抽象了数据模型，并决定能否通过搜索实现业务目标。此外，由于插入 Collections 的每一行数据都必须遵循 Schema，因此有助于保持数据的一致性和长期质量。从技术角度看，定义明确的 Schema 会带来组织良好的列数据存储和更简洁的索引结构，从而提升搜索性能。

一个 Collection Schema 有一个主键、最多四个向量字段和几个标量字段。下图说明了如何将文章映射到模式字段列表。

与langchain集成

Milvus | 🦜️🔗 LangChain

使用 Milvus 和 LangChain 的检索增强生成（RAG） | Milvus 文档

本人实现的用于分块后存储入milvus的类

class MilvusStorage:
    """Milvus向量存储管理类
    
    负责将分块后的文档内容存储到Milvus向量数据库中，
    支持向量检索和BM25全文检索。
    """
    
    def __init__(self, 
                 embedding_function: Embeddings,
                 uri: Optional[str] = None, 
                 db_name: Optional[str] = None,
                 token: Optional[str] = None,
                 collection_name: Optional[str] = None):
        """初始化Milvus存储客户端
        
        Args:
            embedding_function: LangChain embedding模型实例（必需）
            uri: Milvus服务地址，默认从环境变量MILVUS_URI获取
            db_name: 数据库名称，默认从环境变量MILVUS_DB_NAME获取
            token: 认证令牌，默认从环境变量MILVUS_TOKEN获取（可选）
            collection_name: 集合名称，默认从环境变量MILVUS_COLLECTION_NAME获取
        """
        # 验证必需参数
        if not embedding_function:
            raise ValueError("embedding_function是必需参数，必须提供LangChain Embeddings实例")
        
        # 从环境变量读取配置，如果参数没有提供的话
        self.uri = uri or os.getenv('MILVUS_URI', 'http://localhost:19530')
        self.db_name = db_name or os.getenv('MILVUS_DB_NAME', 'rag')
        self.token = token or os.getenv('MILVUS_TOKEN') or None
        self.collection_name = collection_name or os.getenv('MILVUS_COLLECTION_NAME', 'chunks')
        
        # 设置embedding函数
        self.embedding_function = embedding_function
        
        # 初始化LangChain Milvus向量存储
        self.vector_store = Milvus(
            embedding_function=self.embedding_function,
            connection_args={
                "uri": self.uri,
                "db_name": self.db_name,
                "token": self.token
            } if self.token else {
                "uri": self.uri,
                "db_name": self.db_name
            },
            collection_name=self.collection_name,
            index_params={"index_type": "HNSW", "metric_type": "COSINE", "params": {"M": 16, "efConstruction": 200}}
        )
        
    def store_chunks(self, chunk_result: ChunkResult) -> Dict[str, Any]:
        """存储分块结果到Milvus
        
        Args:
            chunk_result: 分块结果对象
            
        Returns:
            Dict: 插入结果，包含插入状态和记录数
            
        Raises:
            ValueError: 当向量存储未初始化时
            Exception: Milvus操作异常
        """
        if not self.vector_store:
            raise ValueError("向量存储未初始化")
        
        if not chunk_result.chunks:
            return {
                "status": "success", 
                "inserted_count": 0,
                "message": "无数据需要插入"
            }
        
        try:
            # 转换为LangChain Document格式
            documents = self._convert_chunks_to_langchain_docs(chunk_result)
            
            # 为每个文档生成UUID作为主键
            from uuid import uuid4
            uuids = [str(uuid4()) for _ in range(len(documents))]
            
            # 使用LangChain Milvus添加文档，指定IDs
            ids = self.vector_store.add_documents(documents=documents, ids=uuids)
            
            return {
                "status": "success",
                "inserted_count": len(documents),
                "document_ids": ids,
                "document_name": chunk_result.document_name,
                "strategy": chunk_result.strategy.value,
                "collection_name": self.collection_name
            }
            
        except Exception as e:
            raise Exception(f"Milvus插入失败: {str(e)}")
    
    def _convert_chunks_to_langchain_docs(self, chunk_result: ChunkResult) -> List[Document]:
        """为现有Documents添加存储所需的元数据
        
        Args:
            chunk_result: 分块结果，chunks已经是Document列表
            
        Returns:
            List[Document]: 添加了元数据的Document列表
        """
        documents = []
        
        for idx, chunk in enumerate(chunk_result.chunks):
            # 创建符合Milvus集合schema的元数据
            # 注意：page_content会自动映射到text_content字段
            updated_metadata = {
                **chunk.metadata,  # 保留原有元数据
                "document_name": chunk_result.document_name,
                "chunk_index": idx,
                "chunk_size": len(chunk.page_content)
            }
            
            # 创建新Document以避免修改原始数据
            # LangChain会自动将page_content映射到Milvus的text_content字段
            # embedding字段会由embedding_function自动生成
            doc = Document(
                page_content=chunk.page_content,
                metadata=updated_metadata
            )
            documents.append(doc)
        
        return documents
    
    def store_chunks_batch(self, chunk_results: List[ChunkResult]) -> Dict[str, Any]:
        """批量存储多个分块结果到Milvus
        
        Args:
            chunk_results: 分块结果列表
            
        Returns:
            Dict: 批量插入结果
            
        Raises:
            ValueError: 当向量存储未初始化时
            Exception: Milvus操作异常
        """
        if not self.vector_store:
            raise ValueError("向量存储未初始化")
        
        if not chunk_results:
            return {
                "status": "success",
                "message": "没有分块结果需要存储",
                "total_chunks": 0,
                "document_count": 0
            }
        
        try:
            # 收集所有文档
            all_documents = []
            total_chunks = 0
            
            for chunk_result in chunk_results:
                if chunk_result.chunks:
                    documents = self._convert_chunks_to_langchain_docs(chunk_result)
                    all_documents.extend(documents)
                    total_chunks += len(documents)
            
            if not all_documents:
                return {
                    "status": "success",
                    "message": "没有文档需要存储",
                    "total_chunks": 0,
                    "document_count": len(chunk_results)
                }
            
            # 为所有文档生成UUID作为主键
            from uuid import uuid4
            uuids = [str(uuid4()) for _ in range(len(all_documents))]
            
            # 批量添加所有文档，指定IDs
            ids = self.vector_store.add_documents(documents=all_documents, ids=uuids)
            
            return {
                "status": "success",
                "message": f"成功存储 {len(chunk_results)} 个文档的 {total_chunks} 个分块",
                "total_chunks": total_chunks,
                "document_count": len(chunk_results),
                "ids": ids,
                "collection_name": self.collection_name
            }
            
        except Exception as e:
            raise Exception(f"Milvus批量插入失败: {str(e)}")
    
    def delete_document(self, 
                       document_name: str, 
                       collection_name: Optional[str] = None) -> Dict[str, Any]:
        """删除指定文档的所有chunks
        
        Args:
            document_name: 文档名称
            collection_name: collection名称
            
        Returns:
            Dict: 删除结果
        """
        target_collection = collection_name or self.collection_name
        
        try:
            if not self.vector_store:
                raise ValueError("向量存储未初始化")
            
            # 使用LangChain Milvus删除功能
            # 注意：LangChain Milvus可能不支持按元数据过滤删除，这里提供基本实现
            return {
                "status": "error",
                "document_name": document_name,
                "error": "LangChain Milvus不支持按文档名删除，请使用其他方式",
                "collection_name": target_collection
            }
            
        except Exception as e:
            return {
                "status": "error", 
                "document_name": document_name,
                "error": str(e)
            }
    
    def get_document_stats(self, 
                          document_name: Optional[str] = None,
                          collection_name: Optional[str] = None) -> Dict[str, Any]:
        """获取文档统计信息
        
        Args:
            document_name: 文档名称，None则统计所有文档
            collection_name: collection名称
            
        Returns:
            Dict: 统计信息
        """
        target_collection = collection_name or self.collection_name
        
        try:
            if not self.vector_store:
                raise ValueError("向量存储未初始化")
            
            # 使用LangChain Milvus获取基本信息
            # 注意：LangChain Milvus没有直接的统计方法，这里提供基本信息
            return {
                "status": "success",
                "collection_name": target_collection,
                "vector_store_type": "LangChain Milvus",
                "embedding_function": str(type(self.embedding_function).__name__),
                "connection_uri": self.uri,
                "database_name": self.db_name,
                "message": "详细统计信息需要通过其他方式获取"
            }
                
        except Exception as e:
            return {
                "status": "error",
                "error": str(e)
            }

基本ANN搜索

近似近邻（ANN）搜索以记录向量嵌入排序顺序的索引文件为基础，根据接收到的搜索请求中携带的查询向量查找向量嵌入子集，将查询向量与子群中的向量进行比较，并返回最相似的结果。

ANN 和 k-Nearest Neighbors (kNN) 搜索是向量相似性搜索的常用方法。在 kNN 搜索中，必须将向量空间中的所有向量与搜索请求中携带的查询向量进行比较，然后找出最相似的向量，这既耗时又耗费资源。

与 kNN 搜索不同，ANN 搜索算法要求提供一个索引文件，记录向量 Embeddings 的排序顺序。当收到搜索请求时，可以使用索引文件作为参考，快速找到可能包含与查询向量最相似的向量嵌入的子组。然后，你可以使用指定的度量类型来测量查询向量与子组中的向量之间的相似度，根据与查询向量的相似度对组成员进行排序，并找出前 K 个组成员。

ANN 搜索依赖于预建索引，搜索吞吐量、内存使用量和搜索正确性可能会因选择的索引类型而不同。您需要在搜索性能和正确性之间取得平衡。

混合检索

多向量混合搜索 | Milvus 文档

让我们考虑一个真实世界的使用案例，其中每个产品都包含文字描述和图片。根据可用数据，我们可以进行三种类型的搜索：

语义文本搜索：这涉及使用密集向量查询产品的文本描述。可以使用BERT和Transformers等模型或OpenAI 等服务生成文本嵌入。
全文搜索：在这里，我们使用稀疏向量的关键词匹配来查询产品的文本描述。BM25等算法或BGE-M3或SPLADE等稀疏嵌入模型可用于此目的。
多模态图像搜索：这种方法使用带有密集向量的文本查询对图像进行查询。可以使用CLIP 等模型生成图像嵌入。

混合检索的构建流程：

创建具有多个向量场的 Collections
- 定义 Collections Schema
- 配置索引参数
- 创建 Collections
插入数据‘
执行混合搜索
- 创建多个 AnnSearchRequest 实例
  
  混合搜索是通过在hybrid_search() 函数中创建多个AnnSearchRequest 来实现的，其中每个AnnSearchRequest 代表一个特定向量场的基本 ANN 搜索请求。因此，在进行混合搜索之前，有必要为每个向量场创建一个AnnSearchRequest 。
- 配置 Rerankers 策略

Rerankers 策略

RRF 排序器 | Milvus 文档

要对 ANN 搜索结果集进行合并和重新排序，选择适当的重新排序策略至关重要。Milvus 提供两种重排策略：

加权排名：如果结果需要强调某个向量场，请使用该策略。WeightedRanker 可以为某些向量场赋予更大的权重，使其更加突出。
RRFRanker（互易排名融合排名器）：在不需要特别强调的情况下选择此策略。RRFRanker 能有效平衡每个向量场的重要性。

加权排名

加权排名器通过为每个搜索路径分配不同的重要性权重，智能地组合来自多个搜索路径的结果并确定其优先级。与技艺高超的厨师平衡多种配料以制作完美菜肴的方式类似，加权排名器也会平衡不同的搜索结果，以提供最相关的综合结果。这种方法非常适合在多个向量场或模式中进行搜索，其中某些场对最终排名的贡献应比其他场更大。

RRFRanker

互惠排名融合（RRF）排名器是 Milvus 混合搜索的一种重新排名策略，它根据多个向量搜索路径的排名位置而不是原始相似度得分来平衡搜索结果。就像体育比赛考虑的是球员的排名而不是个人统计数据一样，RRF Ranker 根据每个项目在不同搜索路径中的排名高低来组合搜索结果，从而创建一个公平、均衡的最终排名。

RRF Ranker 专门设计用于混合搜索场景，在这种场景中，您需要平衡来自多个向量搜索路径的结果，而无需分配明确的重要性权重。

多租户

实施多租户 | Milvus 文档

Milvus 支持四个级别的多租户：数据库、Collection、Partition 和Partition Key。

数据库级	Collections 级	分区级	分区 Key 级
数据隔离	物理	物理	物理	物理 + 逻辑
最大租户数	默认为 64 个。您可以通过修改 Milvus.yaml 配置文件中的`maxDatabaseNum` 参数来增加租户数。	默认为 65,536。可以通过修改 Milvus.yaml 配置文件中的`maxCollectionNum` 参数来增加。	每个 Collection 最多 1,024 个。	百万
数据 Schema 灵活性	高	中	低	低
RBAC 支持	支持	支持	支持	不支持
搜索性能	强	强	中等	中等
跨租户搜索支持	不支持	支持	支持	是
支持有效处理冷热数据	是	是	支持	否目前不支持 Partition Key 级策略。

比较有意思的教程

多模态rag用 Milvus 制作多模态 RAG | Milvus 文档

使用 Milvus 进行文本到图像搜索 | Milvus 文档

使用 Milvus 搜索图像 | Milvus 文档

深度学习

发表于 2025-09-08 更新于 2025-10-24 分类于大三上，深度学习

交叉熵

交叉熵（Cross-Entropy）主要用于衡量两个概率分布之间的差异。在分类任务中，它被广泛用作损失函数，来评估模型预测结果与真实标签之间的“不匹配程度”。

信息量（Information Content）

一个事件 ( x ) 发生的概率为 ( p(x) )，其信息量定义为： [ I(x) = -p(x) ] - 概率越小的事件，发生时带来的信息量越大（比如“太阳从西边升起”）。 - 单位通常是 比特（bit）（以 2 为底）或 纳特（nat）（以自然对数 ( e ) 为底）。

熵（Entropy）

熵是一个概率分布的平均信息量，表示该分布的不确定性： [ H(p) = -_{x} p(x) p(x) ] - 熵越大，不确定性越高（比如公平硬币的熵比偏硬币大）。

交叉熵（Cross-Entropy）

现在有两个分布： - 真实分布 ( p(x) )（比如真实标签） - 模型预测分布 ( q(x) )（比如神经网络输出的概率）

交叉熵衡量的是：当我们用分布 ( q ) 来编码来自分布 ( p ) 的事件时，平均需要多少比特。

数学定义为： [ H(p, q) = -_{x} p(x) q(x) ]

🔍 注意：交叉熵 ≠ 熵。
- 熵：( H(p) = -p p )
- 交叉熵：( H(p, q) = -p q )

Sigmoid的交叉熵损失函数

Sigmoid 的交叉熵损失函数（通常称为 二元交叉熵损失，Binary Cross-Entropy Loss）是用于二分类问题中，结合 Sigmoid 激活函数使用的损失函数。

在二分类任务中，模型输出一个实数值 ( z )（logit）。
通过 Sigmoid 函数将其映射到概率区间 ([0, 1])： [ = (z) = ] 其中 () 表示预测为正类（标签为 1）的概率。
真实标签 ( y {0, 1} )。

二元交叉熵损失（Binary Cross-Entropy, BCE）

对于单个样本，损失函数定义为：

[ (y, ) = -]

其中： - 若 ( y = 1 )，损失为 ( -() ) - 若 ( y = 0 )，损失为 ( -(1 - ) )

Softmax 的交叉熵损失函数

Softmax 函数

给定 logits 向量 ( = [z_1, z_2, …, z_C] )（C 为类别数），Softmax 输出预测概率：

[ _i = (z_i) = ]

交叉熵损失（单个样本）

真实标签为 one-hot 向量 ( = [y_1, y_2, …, y_C] )，其中只有真实类别位置为 1，其余为 0。

损失函数为：

[ = -_{i=1}^{C} y_i (_i) ]

由于 ( y_i ) 只有一个为 1（设真实类别为 ( c )），上式简化为：

[ = -(_c) = -( ) ]

进一步化简：

[ = -z_c + ( _{j=1}^{C} e^{z_j} ) ]

Sigmoid和Softmax区别

1.Sigmoid（逐元素）

对输入 ( x )（标量或向量中的每个元素）： [ (x) = (0, 1) ]

📌 如果输入是向量 ( = [x_1, x_2, …, x_n] )，则输出： [ [(x_1), (x_2), …, (x_n)] ] 每个元素独立计算，彼此无关。

2. Softmax（整体归一化）

对输入向量 ( = [z_1, z_2, …, z_C] )： [ (z_i) = (0, 1) ]

✅ 满足：( _{i=1}^{C} (z_i) = 1 )

应用场景对比

Sigmoid 适用场景：

多标签分类（Multi-label）

每个样本可属于多个类别（如一张图同时有“猫”和“狗”）
输出 C 个独立概率，每个用 Sigmoid 判断是否属于该类
例如：输出 [0.9, 0.2, 0.8] 表示属于类别 0 和 2

Softmax 适用场景：

多分类问题（Multi-class, 互斥）

每个样本只属于一个类别（如 MNIST 手写数字 0~9）
输出 C 个概率，和为 1，最大值对应预测类别
例如：输出 [0.1, 0.7, 0.2] 表示最可能是类别 1

简单来说

“多选一” → Softmax

“可多选” 或 “是/否” → Sigmoid

为什么多分类要用 Softmax，而不是对每个类别用 Sigmoid 再取最大值？

问题在于 损失函数：

如果你用 Binary Cross-Entropy (BCE)（Sigmoid 的配套损失）：

损失 = - [y₁·log(p₁) + y₂·log(p₂) + y₃·log(p₃)]
对于标签 [0, 1, 0]，损失只惩罚“狗”的预测（希望 p₂→1），但不惩罚“猫”和“鸟”是否太高！
结果：模型可能输出 [0.9, 0.95, 0.8]，虽然选对了“狗”，但对其他类也过于自信，泛化差。

而 Softmax + Cross-Entropy：

损失 = -log(p₂)
但因为 p₂ = e^{z₂}/(e^{z₁}+e^{z₂}+e^{z₃})，要让 p₂ 变大，必须让 z₂ 相对于 z₁、z₃ 更大。
所以模型会主动压制错误类别的 logit，学习更清晰的决策边界。

参考资料

《动手学深度学习》 — 动手学深度学习 2.0.0 documentation

课程安排 - 动手学深度学习课程

邀请码

邀请链接

数据的规范化

RobustScaler (鲁棒标准化)与Z-score 标准化（Standardization）对比

Apriori算法

例子

FP-growth

FP-growth 的核心思想（分两步）

模型评价指标

课后第一，二次作业

判断极大频繁项集（M）

判断闭频繁项集（C）

课后第三次作业

用户和权限管理

创建四个系统用户

为四个用户设置密码

创建共享目录

创建用户组并添加成员

修改共享目录的所有权

修改 work 目录的权限

尝试以 bob 用户身份在 work 目录下创建文件

尝试以 john 的身份查看或修改 bob.txt

尝试以 mike 的身份查看或修改 bob.txt

进程管理与调试

编写 badproc.sh 脚本

添加可执行权限

在后台运行脚本

查看进程号

杀死进程

删除脚本运行时创建的目录和文件

创建源文件 fork.c

编译程序（带调试信息）

先运行一次，看看效果

用 gdb 调试 fork 程序

Linux编程环境熟悉

C++编译

创建小型函数库

作业一

1

2

3

作业二

1

2

3

作业三

1

2

3

作业四

1

2

3

作业五

前言

读写

读入图像

存入图像

读图并转 double

图像操作

反色

提取通道

合并通道

二值化（阈值 0.3）

从RGB颜色空间转换成HSI颜色空间

matlab基本操作

获取图像行列和通道数

截取图像

人脸肤色检测

YCrCb 阈值法

HSV 阈值法

椭圆模型法

将彩色图像 Image1 的 R、B 通道互换

使用或操作，进行图像的嵌入

利用单尺度和多尺度 Retinex 增强方法实现图像增强

直方图均衡化计算

landingpage的组成

PPtYoda技术调用

后续任务

docker部署

编写 `badproc.sh` 脚本

创建源文件 `fork.c`

用 `gdb` 调试 fork 程序