计算机系统基础期末笔记汇总
笔记












时钟频率(f) :单位时间内完成的时钟周期数,单位为赫兹(Hz)。 例如:800MHz 表示每秒完成 800×106 个周期。
时钟周期(T) :完成一个时钟周期所需的时间,单位为秒(s)。 例如:800MHz 的时钟周期为 T=800×1061s=1.25ns (纳秒)。
CPI(Cycles Per Instruction,每条指令所需的时钟周期数)是衡量计算机体系结构性能的关键指标之一,用于描述CPU执行一条指令平均需要多少个时钟周期。它直接影响程序的执行速度和系统性能。
MIPS(Million Instructions Per Second) 是衡量计算机处理器性能的一个经典指标,表示 每秒执行的百万条指令数,用于量化 CPU 的指令处理能力。其核心思想是:数值越大,性能越强,但需注意其局限性。
举例:
- 若 CPU 主频为 2 GHz(2×10⁹ Hz),平均
CPI=4,则:
$$
\text{MIPS} = \frac{2 \times 10^9}{4 \times 10^6} = 500 \text{ MIPS}
$$
数量级:
G,吉,十的九次方
n,纳,十的负九次方
m(milli,毫)的数量级是 10−3 (千分之一) 。
1. 补码的定义
补码(Two’s Complement)是计算机中表示有符号整数的标准方法,其核心作用是将减法运算转化为加法运算,从而简化硬件设计。
2. 如何求一个数的补码?
以 8位二进制 为例: - 正数:补码 =
原码(符号位为0,其余位直接表示数值)。
例如:+5 的补码是 00000101。
-5 的补码:
10000101(符号位为1,其余位为5的二进制)。11111010(反码)。11111010 + 1 = 11111011(补码)。3. 数学原理:模运算
补码的本质是基于 模(Modulo)运算。
- 对于 n位二进制数,其模为 2n。
- 负数的补码表示为:
−x ≡ 2n − x (mod 2n)
例如,8位二进制数的模是 28 = 256,因此:
−5 的补码 = 256 − 5 = 251,二进制表示为
11111011。
4. 为什么“取反 + 1”有效?
以 -5 为例(8位): 1.
原码:10000101(符号位为1,数值部分为5)。 2.
取反:11111010(数值部分取反,符号位保留)。 3.
加1:11111010 + 1 = 11111011,即 251 = 256 − 5。
5. 补码的优势
00000000),而原码和反码存在
+0 和 -0 的问题。5 - 3 = 5 + (-3),直接通过补码相加即可。6. 特殊情况:最小负数
对于 n位补码,能表示的范围是:
[−2n − 1, 2n − 1 − 1]
- 例如,8位补码范围是:-128(10000000)到
+127(01111111)。 -
最小负数(-128) 没有对应的正数(因为 +128 超出范围),其补码直接定义为
10000000,无法通过“取反 + 1”从原码推导(因为原码中不存在
+128)。
1. 移码的定义
移码是一种带偏移量的编码方式,主要用于表示浮点数的阶码(Exponent)。其核心思想是将真值(实际数值)加上一个固定的偏移量(Bias),使得所有数值映射到非负数范围,从而简化比较和运算。
公式:
移码 = 真值 + 偏移量
2. 移码的核心作用
3. 偏移量的选择
偏移量通常为 2n − 1 或 2n − 1 − 1(n 为位数): -
单精度浮点数(32位):偏移量为 127(即 27 − 1)。
- 双精度浮点数(64位):偏移量为 1023(即 210 − 1)。
4. 移码与补码的关系
10000000(−128)的移码为 00000000(−128 + 128 = 0)。00000000(0)的移码为 10000000(0 + 128 = 128)。5. 移码的应用场景
【CSAPP-深入理解计算机系统】2-4.浮点数(上)_哔哩哔哩_bilibili
【计算机知识】定点数与浮点数(2)浮点数法表示方法!_哔哩哔哩_bilibili
【计算机基础】进制转换(3) 小数部分如何进行转换?_哔哩哔哩_bilibili
浮点数加减法运算 白中英计算机组成原理期末速成_哔哩哔哩_bilibili
(自用)计算机组成原理 题型三 浮点数加减法运算题_哔哩哔哩_bilibili
浮点运算(浮点数加减运算)计算机组成原理(看了包会)_哔哩哔哩_bilibili
ieee
计算机组成原理期末复习(5分钟):IEEE754浮点数加减计算!_哔哩哔哩_bilibili
short 16位
【CSAPP-深入理解计算机系统】3-9.结构体与联合体_哔哩哔哩_bilibili
【CSAPP-深入理解计算机系统】3-8.数组的分配和访问_哔哩哔哩_bilibili
【CSAPP-深入理解计算机系统】3-7. 过程(函数调用)_哔哩哔哩_bilibili
AT&T格式是汇编语言中的一种语法风格,主要用于x86/x64架构的汇编代码编写。它与Intel格式并列为最常见的两种汇编语法,两者在语法细节上有显著差异。以下是AT&T格式的核心特点、示例及常见用途:
主要特点
| 特性 | AT&T格式语法 | 对比Intel格式语法 |
|---|---|---|
| 寄存器 | 前缀 %(如 %eax) |
无前缀(如 eax) |
| 立即数 | 前缀 $(如 $0x10) |
直接使用数值(如 10) |
| 操作数顺序 | 源操作数在前,目标在后 | 目标在前,源在后 |
| 内存寻址 | offset(base, index, scale) |
[base + index*scale + offset] |
| 指令后缀 | 通过后缀标明操作数大小(如 l 表示32位) |
无后缀,由操作数推断 |
EAX, EBX, ECX, EDX 均为 32 位寄存器AX, BX, CX, DX 均为 16 位寄存器AH, BH, CH, DH 均为高 8 位寄存器AL, BL, CL, DL 均为低 8 位寄存器1. 基础内存寻址模式
(1) 直接寻址(Direct Addressing) cccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccccc
offset(AT&T格式)或
[offset](Intel格式)。1 | movl var(%rip), %eax # AT&T格式(RIP相对寻址,64位模式推荐) |
1 | mov eax, [var] # Intel格式(32位模式) |
(2) 寄存器间接寻址(Register Indirect Addressing)
(base_register) 或
[base_register]1 | movl (%eax), %ebx # 将EAX指向的内存值传入EBX |
1 | mov ebx, [eax] |
(3) 基址寻址(Base Addressing)
offset(base_register) 或
[base_register + offset]1 | movl 8(%ebp), %ecx # 从栈帧偏移8处读取数据到ECX |
1 | mov ecx, [ebp + 8] |
(4) 变址寻址(Indexed Addressing)比例寻址
语法:array(, index_register, scale)
或 [array + index_register*scale]
用途:数组元素访问。
示例:
1 | movl array(,%eax,4), %edx # 数组array + EAX*4位置的值传入EDX(数组索引) |
1 | mov edx, [array + eax*4] |
2. 组合寻址模式
(1) 基址 + 变址(Base + Index)
语法:(base_register, index_register)
或 [base_register + index_register]
用途:访问二维数组或动态分配的数组。
示例:
1 | movl (%ebx, %esi), %edi # 将EBX + ESI指向的内存值传入EDI |
1 | mov edi, [ebx + esi] |
**(2) 基址 + 比例变址(Base + Index*Scale)**
(base_register, index_register, scale)
或 [base_register + index_register*scale]1 | movl (%ebx, %esi, 4), %edi # 将EBX + ESI*4指向的内存值传入EDI(4字节元素) |
1 | mov edi, [ebx + esi*4] |
**(3) 基址 + 比例变址 + 偏移(Base + Index*Scale + Offset)**
offset(base_register, index_register, scale)
或 [base_register + index_register*scale + offset]1 | movl 12(%ebx, %esi, 8), %edi # 结构体数组中第ESI个元素的偏移12处数据传入EDI |
1 | mov edi, [ebx + esi*8 + 12] |
3.总结
| 寻址模式 | AT&T格式语法 | Intel格式语法 |
|---|---|---|
| 直接寻址 | var(%rip) |
[rip + var](64位)或 var |
| 寄存器间接寻址 | (%eax) |
[eax] |
| 基址寻址 | 8(%ebp) |
[ebp + 8] |
| 变址寻址 | array(,%eax,4) |
[array + eax*4] |
| 基址+比例变址 | (%ebx, %esi, 4) |
[ebx + esi*4] |
| 基址+比例变址+偏移 | 12(%ebx, %esi, 8) |
[ebx + esi*8 + 12] |
在 AT&T 汇编格式中,指令后缀(如
b、w、l、q)用于明确操作数的大小,确保汇编器正确生成机器码。判断后缀的核心规则是:根据操作数的大小选择对应的后缀,尤其是寄存器的位数或内存操作数的显式指定。以下是详细说明:
后缀与操作数大小的对应关系
| 后缀 | 操作数大小 | 示例寄存器/操作数 |
|---|---|---|
b |
byte(8位) | %al, $0x10,
12(%ebp)(需显式指定) |
w |
word(16位) | %ax, %bx,
12(%ebp)(需显式指定) |
l |
long(32位) | %eax, %ebx,
12(%ebp)(需显式指定) |
q |
quad(64位) | %rax, %rbx,
12(%ebp)(需显式指定) |
立即数默认为32位
(1)%edx:临时变量
%edx
读取数据,不涉及内存地址的间接访问。%edx 存储的是某个局部变量或计算结果(如
temp = a + b),则对应临时变量。(2)(%ecx):指针
%ecx
中存储的是内存地址,(%ecx) 表示解引用该地址(类似C语言的
*ptr)。%ecx 存储的是一个指针变量(如
int *ptr),则 (%ecx)
对应指针解引用。关键结论
| 操作数 | 类型 | 判断依据 |
|---|---|---|
%edx |
临时变量 | 直接从寄存器读取数据,无间接内存访问(无括号)。 |
(%ecx) |
指针 | 使用括号 (%ecx) 表示解引用内存地址(类似C语言的
*ptr)。 |
常见模式对比
| 汇编指令 | C语言对应操作 | 解释 |
|---|---|---|
movl %eax, (%ebx) |
*ptr = temp; |
%ebx 是指针(存储地址),%eax
是临时变量。 |
movl (%ebx), %eax |
temp = *ptr; |
从指针 ptr 读取值到临时变量 temp。 |
movl $0x1, %eax |
temp = 1; |
%eax 是临时变量,直接赋值。 |
在汇编语言中,M 通常表示
内存(Memory),用于指示操作数来自内存地址。在你的问题中,M[R[eax]]
的含义是:
M 的作用
M[地址] 表示从 内存地址为
地址 的位置读取数据。R[eax] 表示寄存器 EAX
的值(即 EAX 中存储的内容)。M[R[eax]] 的含义是: > 以
EAX
寄存器的值作为内存地址,从该地址读取数据。** AT&T 汇编中的等价写法**
在 AT&T 汇编语法中,M[R[eax]] 对应的写法是:
1
addl (%eax), %edx
(%eax):以
EAX 的值为内存地址,读取该地址的内容(默认是 4 字节,即 32
位)。 - addl:执行 32 位加法。 -
%edx:目标寄存器,存储结果。
关键点总结
| 符号 | 含义 | 示例 |
|---|---|---|
R |
寄存器(Register) | R[eax] → EAX 的值 |
M |
内存(Memory) | M[地址] → 从地址读取数据 |
() |
AT&T 汇编中表示内存寻址 | (%eax) → 等价于 M[R[eax]] |
| 指令类型 | 操作目的 | 影响标志位 | 典型用途 |
|---|---|---|---|
addl |
加法 | OF, SF, ZF, CF | 数值运算、地址偏移 |
subl |
减法 | OF, SF, ZF, CF | 数值运算、条件判断 |
orl |
按位或 | OF=0, SF, ZF, CF=0 | 位掩码操作 |
testl |
按位与测试 | OF=0, SF, ZF, CF=0 | 条件判断(如检查位是否设置) |
imull |
有符号乘法 | OF, CF | 数值运算 |
leal |
地址计算 | 无影响 | 高效数组索引计算 |
decl |
递减 | OF, SF, ZF, CF | 循环计数、边界检查 |
sall(Shift Arithmetic Left)——
左移指令
功能
and(Logical AND)—— 逻辑与指令
功能
shrl 是 逻辑右移指令 (Shift Right
Logical),用于对操作数进行 无符号右移 ,即高位补
0,低位移出。
leal 是 加载有效地址(Load Effective
Address) 的指令,其功能是
计算内存地址并存储到目标寄存器 ,但
不会访问内存 。它常用于 地址计算 和
高效算术运算
以下是 x86/x64 架构中常见的四个状态标志位(OF、SF、ZF、CF)的详细说明及其判断方法:
1. 标志位概述
| 标志 | 全称 | 含义 |
|---|---|---|
| CF | Carry Flag | 无符号溢出标志:表示无符号数运算是否产生进位或借位。 |
| ZF | Zero Flag | 零标志:表示运算结果是否为零。 |
| SF | Sign Flag | 符号标志:表示运算结果的最高位(符号位)是否为1(负数)。 |
| OF | Overflow Flag | 溢出标志:表示有符号数运算是否溢出(结果超出数据类型表示范围)。 |
2. 判断方法详解
(1) 进位标志(CF)
(2) 零标志(ZF)
(3) 符号标志(SF)
(4) 溢出标志(OF)
【CSAPP-深入理解计算机系统】3-3.栈与数据传送指令_哔哩哔哩_bilibili
1. 参数压栈顺序
C语言默认使用 cdecl
调用约定,参数从右到左压入栈中。例如,函数调用
operate(x, y, z, k) 的压栈顺序为: 1
2
3
4
5push k; // 第四个参数(最右边)
push z; // 第三个参数
push y; // 第二个参数
push x; // 第一个参数(最左边)
call operate;1
2
3
4
5
6
7高地址
| k (参数4) | ← 栈顶(ESP)
| z (参数3) |
| y (参数2) |
| x (参数1) |
| 返回地址 |
低地址
2. 栈帧建立过程
进入函数 operate 后,通过以下指令建立栈帧:
1
2pushl %ebp ; 保存旧的EBP(栈帧基址)
movl %esp, %ebp ; 将当前栈顶(ESP)赋值给EBP,作为新栈帧的基址1
2
3
4
5
6
7
8高地址
| k (参数4) | ← EBP + 20
| z (参数3) | ← EBP + 16
| y (参数2) | ← EBP + 12
| x (参数1) | ← EBP + 8
| 返回地址 | ← EBP + 4
| 旧 EBP | ← EBP
低地址
3. 参数地址的计算逻辑
EBP + 4:返回地址(由
call 指令自动压栈)。EBP + 8:第一个参数(x)。EBP + 12:第二个参数(y)。EBP + 16:第三个参数(z)。EBP + 20:第四个参数(k)。原因:
1.
参数顺序:参数从右到左压栈,导致第一个参数(x)位于栈的最低地址(EBP + 8),而第四个参数(k)位于最高地址(EBP + 20)。
2. 偏移计算:每个参数占用4字节(32位系统中
int 和指针大小),因此偏移量依次递增4。
3. 栈帧基址:EBP 指向旧的 EBP
值,其上方是返回地址(EBP + 4),再上方是参数。
超硬核!408考研重点!汇编语言表示程序函数的过程调用!23王道计算机组成原理指令系统_哔哩哔哩_bilibili
反汇编代码是将二进制机器码(如可执行文件、内存转储)转换为 人类可读的汇编指令 的结果。它是逆向工程、漏洞分析、调试等领域的核心工具。以下是详细说明:
1. 反汇编代码的定义
2. 反汇编代码的典型格式
反汇编代码通常包含以下部分: | 字段 |
说明 | 示例 | | ————————- |
————————————————– | —————————- | | 地址(Address) |
指令在内存中的地址(十六进制)。 | 0x804838c | |
机器码(Opcode) |
对应的原始十六进制机器码(机器指令的二进制表示)。 | 74 08
| | 汇编指令(Mnemonic) | 汇编助记符(如
mov, jmp, call)及操作数。 |
je 0x8048396 | | 注释(Comment, 可选) |
开发者添加的注释(某些工具会自动生成符号信息)。 |
; if (eax == 0) goto label |
示例反汇编代码(AT&T格式)
1 | 0804838c <main>: |
小端方式(Little-Endian) 是一种 数据在内存中的存储顺序,其核心特点是: > 数据的低位字节(LSB, Least Significant Byte)存储在内存的低地址处,高位字节(MSB, Most Significant Byte)存储在高地址处。
1. 小端 vs 大端
| 特性 | 小端(Little-Endian) | 大端(Big-Endian) |
|---|---|---|
| 存储顺序 | 低位字节在前(低地址),高位在后 | 高位字节在前(低地址),低位在后 |
| 示例 | 0x12345678 → 存储为 78 56 34 12 |
0x12345678 → 存储为 12 34 56 78 |
| 常见平台 | x86/x64 架构(Intel/AMD 处理器) | ARM(部分模式)、网络协议(TCP/IP) |
2. 小端方式的直观理解
示例:32位整数 0x12345678
1 | 地址 → 0x1000 0x1001 0x1002 0x1003 |
0x78 存储在最低地址
0x1000。0x12 存储在最高地址 0x1003。在 IA-32(x86)架构中,转移目标地址的计算依赖于 指令的长度 和 相对偏移量(Displacement)。以下是详细分析:
1. 转移指令的基本原理
2. 示例:call 指令的地址计算
(1) 已知条件
0x804838e(call
指令的起始地址)。E8 1E 00 00 00。
E8 是 call 的操作码。1E 00 00 00 是偏移量(小端方式存储)。(2) 计算步骤
call 指令占 5 字节(1 字节操作码 + 4
字节偏移量)。0x804838e + 5 = 0x8048393。1E 00 00 00(小端方式)→ 转换为大端顺序为
0x0000001E(十进制 30)。0x8048393 + 0x1E = 0x80483B1。3. 核心公式 目标地址 = (当前指令地址 + 指令长度) + 偏移量
- 当前指令地址:指令的起始地址(如
0x804838e)。 -
指令长度:由操作码和操作数决定(如 call 占
5 字节)。 -
偏移量:从指令的操作数中提取并转换为有符号整数。
9. 其他指令示例
(1) je 指令
1 | 804838c: 74 08 je 0x8048396 |
0x804838c。0x08(单字节,无需反转)。0x804838c + 2 + 0x08 = 0x8048396。(2) jmp 指令
1 | 80483a4: E9 F6 FF FF FF jmp 0x804839f |
0x80483a4。F6 FF FF FF(小端)→ 补码为
-10(十进制)。0x80483a4 + 5 + (-10) = 0x804839f。下一条指令地址=当前指令地址+当前指令长度
【CSAPP-深入理解计算机系统】7-6. 重定位_哔哩哔哩_bilibili
计算机系统基础摘记——程序的链接_引入链接的好处是什么-CSDN博客
【CSAPP-深入理解计算机系统】7-5. 静态库的解析过程_哔哩哔哩_bilibili
gdb调试






方差(Variance)和偏差(Bias)是机器学习中衡量模型性能的两个核心概念,它们共同构成了偏差-方差权衡(Bias-Variance Tradeoff)的基础框架。以下是两者的定义与区别:
1. 偏差(Bias)
2. 方差(Variance)
3. 如何降低偏差与方差
| 目标 | 方法 | 示例 |
|---|---|---|
| 降低偏差 | 增加模型复杂度(如更多特征、更深的神经网络)、减少正则化强度 | 使用多项式回归替代线性回归 |
| 降低方差 | 增加训练数据、引入正则化(L1/L2)、使用集成方法(如 Bagging、Boosting) | 随机森林(Bagging)降低决策树的方差 |
4. 总结
以下是关于监督学习与无监督学习的核心区别总结:
1. 监督学习(Supervised Learning)
任务类型:
-
分类(Classification):预测离散类别标签(如垃圾邮件/非垃圾邮件)。
-
回归(Regression):预测连续数值标签(如房价预测)。
特点:
- 需要带标签的样本(Labeled
Data),即每个训练样本都有明确的输入 $ x $ 和输出 $ y $。
- 模型通过学习输入与标签之间的映射关系进行预测。
2. 无监督学习(Unsupervised Learning)
任务类型:
特点:
- 仅需无标签的样本(Unlabeled
Data),无需预先定义输出目标。
- 模型自主挖掘数据内在结构或分布规律。
本质思想:寻找合适的参数使得「当前的样本情况发生的概率」最大。
又由于假设每一个样本相互独立(概率条件理想的情况下),因此可以用连乘的形式表示上述概率,当然由于概率较小导致连乘容易出现浮点数精度损失,因此尝尝采用取对数的方式来避免「下溢」问题。也就是所谓的「对数似然估计」方法。
在已知样本特征 $ $ 的条件下,选择分类结果 $ c_i $,使得分类的期望损失(Risk)最小。
**(1) 损失函数 $ _{ij} $**
(2) 条件风险(单个样本的期望损失)
对于给定样本 $ $,若将其分类为 $ c_i ,则其 * *条件风险 * *为:$ R(c_i | ) = {j=1}^N {ij} P(c_j | ) $$ - 含义:在已知 $ $ 的情况下,分类为 $ c_i $ 的平均损失。 - 推导: - $ P(c_j | ) $:样本 $ $ 真实属于 $ c_j $ 的后验概率。 - $ {ij} $:若真实类别是 $ c_j $,但被分到 $ c_i $,则产生损失 $ {ij} $。 - 因此,总期望损失是所有可能真实类别的加权和(权重为后验概率)。
(3) 总体风险
对于整个数据集,分类器 $ h() $ 的总体风险为: R(h) = 𝔼x[R(h(x)|x)] = ∫R(h(x)|x)p(x)dx - 含义:所有样本的平均条件风险。h为分类器(模型) - 目标:找到使 $ R(h) $ 最小的分类器 $ h() $。
根据上述定义,贝叶斯决策论的分类规则是: > 对于样本 $ $,选择使其条件风险 $ R(c_i | ) $ 最小的类别 $ c_i $ 作为预测结果。
即: $$ h^*(\mathbf{x}) = \arg\min_{c_i} R(c_i | \mathbf{x}) = \arg\min_{c_i} \sum_{j=1}^N \lambda_{ij} P(c_j | \mathbf{x}) $$
此时条件风险简化为: R(c_i | ) = {j i} P(c_j | ) = 1 - P(c_i | ) $$ 原因:概率之和为 1:$ {j=1}^N P(c_j | ) = 1 $,因此 $ _{j i} P(c_j | ) = 1 - P(c_i | ) $。
此时,最小化风险等价于最大化后验概率,即: h*(x) = arg maxciP(ci|x) 这正是传统贝叶斯分类器的决策规则。
即在x样本的情况下,分类正确的概率最大
后验概率(Posterior Probability)是贝叶斯理论中的核心概念,指的是在观察到新证据(数据)后,对事件发生概率的修正 。 其本质是:
“已知结果(数据),反推原因(类别或参数)的概率” 。
已知结果(数据)B,反推最可能的原因A(后验概率 P(A∣B) )
先验概率是贝叶斯统计中的核心概念,指的是在观察到新数据之前,对某一事件或假设的概率估计。它是基于已有知识、经验或假设得出的初始概率,后续会通过新数据更新为更准确的后验概率。
1. 核心定义
2. 直观理解
(1) 类比:医学诊断
| 模型类型 | 建模目标 | 数学表达 |
|---|---|---|
| 判别式模型 | 直接建模 $ P(c | ) $ |
| 生成式模型 | 先建模联合概率 $ P(, c) $,再推导 $ P(c | ) $ |
1. 判别式模型(Discriminative Model)
2. 生成式模型(Generative Model)
目标:先学习数据的生成过程,即联合概率 $ P(, c) $,再通过贝叶斯定理推导条件概率 $ P(c|) $。
数学步骤:
假设我们要判断一封邮件是否为垃圾邮件($ c=spam $ 或 $ ham $)。
判别式模型(逻辑回归)
直接建模: $$ P(spam|\mathbf{x}) = \frac{1}{1 + e^{-(w^T \mathbf{x} + b)}} $$ 若 $ P(spam|) > 0.5 $,则判定为垃圾邮件。
生成式模型(朴素贝叶斯)
根据概率论的基本定义: $$ P(c|\mathbf{x}) = \frac{P(\mathbf{x}, c)}{P(\mathbf{x})} $$ - 含义: - $ P(, c) $:联合概率,表示特征 $ $ 和类别 $ c $ 同时发生的概率。 - $ P() $:边缘概率(证据),表示特征 $ $ 出现的概率,用于归一化。
根据贝叶斯定理,联合概率 $ P(, c) $ 可以分解为: P(x, c) = P(c) ⋅ P(x|c) 其中: - $ P(c) $:类先验概率(Prior Probability),表示类别 $ c $ 在数据中的整体占比。 - $ P(|c) $:似然度(Likelihood),表示在类别 $ c $ 下,特征 $ $ 出现的概率。
将上述分解代入条件概率公式,得到: $$ P(c|\mathbf{x}) = \frac{P(c) \cdot P(\mathbf{x}|c)}{P(\mathbf{x})} $$ 产生问题:
在贝叶斯分类中,需要计算联合概率 P(x∣c) ,即在类别 c 下,特征向量 x=(x1,x2,…,*x**d) 的条件概率。 若直接建模联合概率,需估计 d* 个特征的所有可能组合的概率。例如:
举例:
结果 : 在高维空间中,训练数据无法覆盖所有可能的特征组合,导致模型无法可靠估计联合概率 P(x∣c) 。
因此产生属性条件独立性假设
朴素贝叶斯分类器的核心思想是通过贝叶斯定理和属性条件独立性假设来简化计算,从而高效地进行分类。
朴素贝叶斯的核心假设是:在已知类别 $ c $
的条件下,所有属性(特征)之间相互独立。
因此,联合概率 $ P(|c) $ 可以分解为各属性独立概率的乘积: $$
P(\mathbf{x}|c) = \prod_{i=1}^d P(x_i|c)
$$ 其中 $ d $ 是特征的数量,$ x_i $ 是第 $ i $ 个特征的取值。
将此代入贝叶斯公式: $$ P(c|\mathbf{x}) = \frac{P(c) \cdot \prod_{i=1}^d P(x_i|c)}{P(\mathbf{x})} $$
在分类任务中,我们的目标是比较不同类别 $ c $ 的后验概率 $ P(c|) $,并选择最大值。由于 $ P() $ 对所有类别来说是相同的常量(与类别无关),因此在最大化过程中可以忽略: $$ \arg\max_{c} P(c|\mathbf{x}) = \arg\max_{c} \left[ \frac{P(c) \cdot \prod_{i=1}^d P(x_i|c)}{P(\mathbf{x})} \right] = \arg\max_{c} \left[ P(c) \cdot \prod_{i=1}^d P(x_i|c) \right] $$ 这就是公式中 $ P() $ 被省略的原因。
在比较的过程中,分母相同,可以忽略
简化后的决策规则为: $$ h_{nb}(\mathbf{x}) = \arg\max_{c} \left[ P(c) \cdot \prod_{i=1}^d P(x_i|c) \right] $$ 即: - 计算每个类别的先验概率 $ P(c) $。 - 计算每个特征在该类别下的条件概率 $ P(x_i|c) $。 - 将这些概率相乘,选择乘积最大的类别作为预测结果。
基于大数定律 $$ P(c) = \frac{|D_c|}{|D|} $$ - 符号含义: - $ D $:训练集,包含所有样本。 - $ D_c $:训练集中类别为 $ c $ 的样本子集。 - $ |D_c| $:类别 $ c $ 的样本数量。 - $ |D| $:训练集总样本数量。
在生成式模型(如朴素贝叶斯分类器)中,条件概率 $ P(x_i | c) $ 表示在类别 $ c $ 下,第 $ i $ 个属性取值为 $ x_i $ 的概率。根据属性类型(离散或连续),其估计方法不同:
1. 离散属性的条件概率估计
公式: $$ P(x_i | c) = \frac{|D_{c,x_i}|}{|D_c|} $$ - 符号含义: - $ D_c $:训练集中类别为 $ c $ 的样本集合。 - $ D_{c,x_i} : D_c $ 中第 $ i $ 个属性取值为 $ x_i $ 的样本子集。 - $ |D_{c,x_i}| : D_{c,x_i} $ 的样本数量。 - $ |D_c| $:类别 $ c $ 的总样本数量。
直观解释:
注意事项:
2. 连续属性的条件概率估计
假设:属性服从正态分布(高斯分布) $$ p(x_i | c) = \frac{1}{\sqrt{2\pi}\sigma_{c,i}} \exp\left( -\frac{(x_i - \mu_{c,i})^2}{2\sigma_{c,i}^2} \right) $$ - 符号含义: - $ {c,i} $:类别 $ c $ 在第 $ i $ 个属性上的均值。 - $ {c,i}^2 $:类别 $ c $ 在第 $ i $ 个属性上的方差。
直观解释:
注意事项:
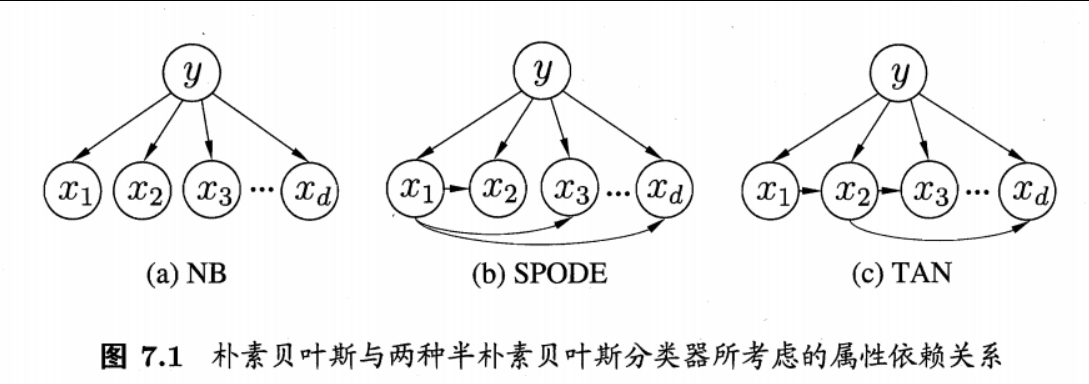
半朴素贝叶斯分类器是对传统朴素贝叶斯的改进,它在保留计算效率的同时,适当引入部分属性间的依赖关系,从而在分类性能和计算复杂度之间取得平衡。
(1) 定义
独依赖估计(One-Dependent Estimator, ODE)是半朴素贝叶斯的一种实现方式,其核心假设是: > 每个属性 $ x_i $ 在类别 $ c $ 之外最多依赖于一个其他属性(称为父属性 $ pa_i $)。
数学表达式为: $$ P(c|\mathbf{x}) \propto P(c) \prod_{i=1}^d P(x_i | c, pa_i) $$ 其中: - $ pa_i $:属性 $ x_i $ 的父属性(依赖的单一属性)。 - $ P(x_i | c, pa_i) $:在类别 $ c $ 和父属性 $ pa_i $ 下,属性 $ x_i $ 的条件概率。
(2) 直观理解
超父独依赖估计(Super Parent One-Dependent Estimator, SPODE)是半朴素贝叶斯分类器的一种扩展,其核心思想是: > 所有属性都依赖于同一个“超父”属性 $ x_i $,从而在保留部分依赖关系的同时避免完全联合概率的计算。
(1) 贝叶斯定理展开 $$ P(c|\mathbf{x}) = \frac{P(\mathbf{x}, c)}{P(\mathbf{x})} $$ 其中: - $ P(, c) $:联合概率,表示特征 $ $ 和类别 $ c $ 同时发生的概率。 - $ P() $:证据(归一化因子)。
(2) 引入“超父”属性 $ x_i $
假设所有属性 $ x_j (j i) $ 在类别 $ c $ 下仅依赖于 $ x_i ,则:$ P(, c) = P(c, x_i) P(x_1, , x_{i-1}, x_{i+1}, , x_d | c, x_i) 进一步分解为: P(, c) = P(c, x_i) _{j i} P(x_j | c, x_i) $$
(3) 最终形式
由于 $ P() $ 对所有类别相同,可忽略,最终决策规则为: $$ P(c|\mathbf{x}) \propto P(c, x_i) \cdot \prod_{j=1}^d P(x_j | c, x_i) $$ 其中: - $ P(c, x_i) $:类别 $ c $ 和属性 $ x_i $ 的联合概率。 - $ P(x_j | c, x_i) $:在类别 $ c $ 和 $ x_i $ 的条件下,属性 $ x_j $ 的概率。
TAN(Tree-Augmented Naive Bayes)是半朴素贝叶斯分类器的一种扩展,旨在通过引入属性间的树状依赖关系,在保留计算效率的同时,显著提升分类性能。它结合了贝叶斯网络的建模能力和生成式模型的概率推理优势。
1. 核心思想
TAN 的核心假设是: > 所有属性(特征)在类别 $ c $ 的基础上,形成一个以属性为节点的树状依赖结构,即每个属性最多依赖一个其他属性(父属性),且整个依赖图是一棵无环的树。
数学表达: $$ P(c|\mathbf{x}) \propto P(c) \cdot \prod_{i=1}^d P(x_i | c, pa_i) $$ 其中: - $ pa_i $:属性 $ x_i $ 的父属性(依赖的单一属性)。 - $ P(x_i | c, pa_i) $:在类别 $ c $ 和父属性 $ pa_i $ 的条件下,属性 $ x_i $ 的条件概率。
2. TAN 的构建步骤
TAN 通过以下步骤构建属性间的依赖结构:
(1) 计算互信息(Mutual Information)
互信息衡量两个属性之间的相关性: $$ I(x_i, x_j) = \sum_{x_i, x_j} P(x_i, x_j) \log \frac{P(x_i, x_j)}{P(x_i)P(x_j)} $$ - 含义:互信息越大,两个属性之间的依赖关系越强。
(2) 构建带权图
(3) 最大带权生成树(Maximum Weight Spanning Tree, MWST)
使用克鲁斯卡尔(Kruskal)算法或普里姆(Prim)算法,选择一棵连接所有属性节点的树,使得: - 树的边权重(互信息)总和最大。 - 树中无环。
(4) 确定依赖方向
待学习
EM算法(Expectation-Maximization Algorithm)是一种迭代优化算法,用于处理含有隐变量(Hidden Variables)或缺失数据的概率模型参数估计问题。它的核心思想是通过交替执行期望(E)步和最大化(M)步,逐步逼近模型参数的最大似然估计。
(1) 什么是隐变量?
隐变量(Latent Variables)是模型中不可观测但影响观测数据的变量。例如: - 混合高斯模型(GMM):每个样本属于哪个高斯分布是隐变量。 - 聚类任务:样本所属的聚类标签是隐变量。
(2) 问题挑战
当存在隐变量时,直接最大化似然函数变得困难。例如: log P(x|θ) = log ∑zP(x, z|θ) 其中 $ z $ 是隐变量,$ $ 是模型参数。由于对数中包含求和,直接求导无法分离参数。
(3) EM算法的解决方案
EM算法通过以下步骤迭代求解: 1. E步(期望):用当前参数估计隐变量的后验分布(即“责任”分配)。 2. M步(最大化):基于隐变量的后验分布,最大化期望似然函数以更新参数。
(1) 初始化参数
选择初始参数 $ ^{(0)} $,例如随机初始化或通过启发式方法设定。
(2) E步:计算隐变量后验分布
给定当前参数 $ ^{(t)} $,计算隐变量 $ z $ 的后验概率: Q(t)(z) = P(z|x, θ(t)) 这一步为每个样本分配隐变量的概率分布(如样本属于某个聚类的概率)。
(3) M步:最大化期望似然
基于 $ Q^{(t)}(z) ,构造期望似然函数并最大化:$ ^{(t+1)} = _{} _z Q^{(t)}(z) P(, z|) $$ 这一步更新参数 $ $,使得期望似然最大。
(4) 收敛判断
重复E步和M步直到参数收敛(如 $ |^{(t+1)} - ^{(t)}| < $)或达到最大迭代次数。
假设数据由多个高斯分布生成,但不知道每个样本属于哪个分布。
(1) 模型定义
(2) E步:计算责任分配
对于每个样本 $ x_i $ 和类别 $ k ,计算责任(responsibility):$ _{ik}^{(t)} = P(z_i=k|x_i, ^{(t)}) = $$ 含义:在当前参数下,样本 $ x_i $ 属于类别 $ k $ 的概率。
(3) M步:更新参数
根据责任 $ _{ik} $ 更新参数: - 均值更新: $$ \mu_k^{(t+1)} = \frac{\sum_{i=1}^N \gamma_{ik}^{(t)} x_i}{\sum_{i=1}^N \gamma_{ik}^{(t)}} $$ - 协方差更新: $$ \Sigma_k^{(t+1)} = \frac{\sum_{i=1}^N \gamma_{ik}^{(t)} (x_i - \mu_k^{(t+1)})(x_i - \mu_k^{(t+1)})^T}{\sum_{i=1}^N \gamma_{ik}^{(t)}} $$ - 权重更新: $$ \pi_k^{(t+1)} = \frac{\sum_{i=1}^N \gamma_{ik}^{(t)}}{N} $$
(4) 迭代终止
当参数变化小于阈值或达到最大迭代次数时停止。
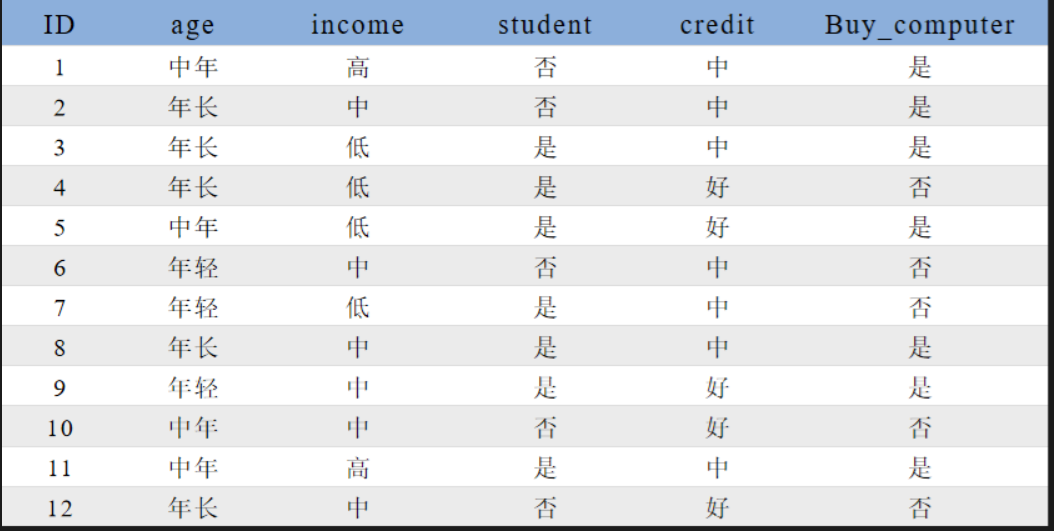

已知观测数据-67,-48,6,8,14,16,23,24,28,29,41,49,56,60,75,试估计两个分量的高斯混合模型的5个参数。

1 | from sklearn.mixture import GaussianMixture |
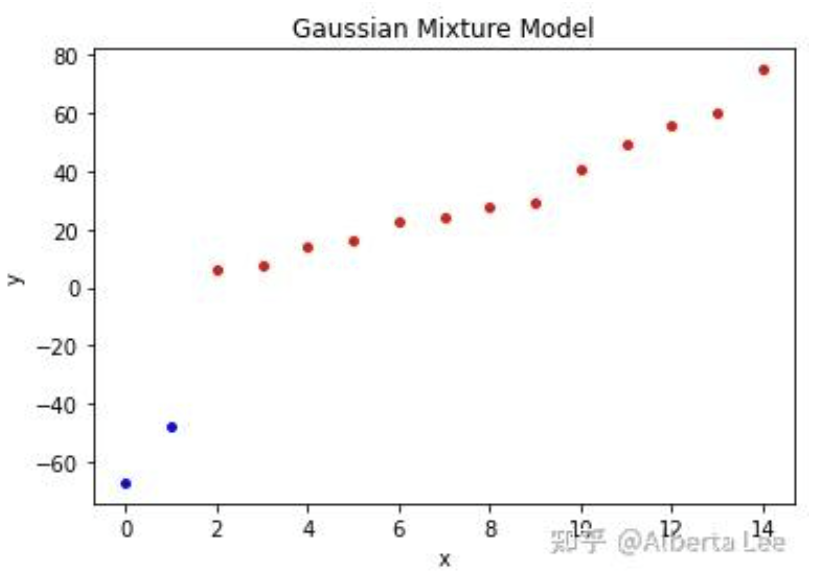
1 | # means = [[ 32.98489643 -57.51107027]] |
简要阐述下EM算法的原理,并给出EM算法对高斯混合模型GMM进行求解的具体过程。
EM算法(期望最大化算法)是一种用于含有隐变量的概率模型参数估计的迭代优化方法。其核心思想是通过交替执行两个步骤来最大化观测数据的似然函数:
EM算法通过不断优化似然函数的下界,最终收敛到局部最优解。以下具体阐述EM算法对高斯混合模型(GMM)的求解过程。
1. GMM模型定义
GMM假设数据由 $ K $ 个高斯分布线性组合生成,其概率密度函数为: $$ p(\mathbf{x}|\theta) = \sum_{k=1}^K \alpha_k \cdot \mathcal{N}(\mathbf{x}|\mu_k, \Sigma_k) $$ 其中: - $ k $:第 $ k $ 个高斯分布的权重($ {k=1}^K _k = 1 $)。 - $ _k $:第 $ k $ 个高斯分布的均值向量。 - $ _k $:第 $ k $ 个高斯分布的协方差矩阵。 - $ = {_k, _k, k}{k=1}^K $:模型参数。
隐变量 $ z_i {1,,K} $ 表示样本 $ _i $ 的类别标签(未知)。
2. EM算法步骤
(1) 初始化参数
随机或通过K-means初始化: - 每个高斯分布的均值 $ _k^{(0)} $、协方差 $ _k^{(0)} $、权重 $ _k^{(0)} $。
(2) 迭代优化(E步与M步)
E步:计算责任(后验概率) 对每个样本 xi 和每个簇 $ k $,计算其属于第 $ k $ 个高斯分布的后验概率 $$ \gamma(z_{ik}) = \frac{\alpha_k \cdot \mathcal{N}(\mathbf{x}_i | \mu_k, \Sigma_k)}{\sum_{j=1}^K \alpha_j \cdot \mathcal{N}(\mathbf{x}_i | \mu_j, \Sigma_j)} $$ 此概率表示在当前参数下,样本 $ _i $ 属于第 $ k $ 个高斯分布的“责任”。
M步:更新参数
基于责任 $ (z_{ik}) $,最大化完全数据似然函数的期望,更新参数:
(3) 收敛判断
计算对数似然函数: $$ \log p(\mathbf{X}|\theta) = \sum_{i=1}^N \log \left( \sum_{k=1}^K \alpha_k \cdot \mathcal{N}(\mathbf{x}_i|\mu_k, \Sigma_k) \right) $$ 若对数似然的变化量小于阈值或达到最大迭代次数,则停止;否则重复E步和M步。。
[5分钟学算法] #06 EM算法 你到底是哪个班级的_哔哩哔哩_bilibili
集成学习(Ensemble Learning)通过构建并结合多个学习器(基模型)来完成学习任务,其核心思想是“优而不同”,即通过多个弱学习器的协作提升整体性能,通常能获得比单一学习器更优的泛化能力 。

在上图的集成模型中,若个体学习器都属于同一类别,例如都是决策树或都是神经网络,则称该集成为同质的(homogeneous);若个体学习器包含多种类型的学习算法,例如既有决策树又有神经网络,则称该集成为异质的(heterogenous)。
同质集成:个体学习器称为“基学习器”(base learner),对应的学习算法为“基学习算法”(base learning algorithm)。
异质集成:个体学习器称为“组件学习器”(component learner)或直称为“个体学习器”。
集成学习的两个重要概念:准确性和多样性(diversity)。准确性指的是个体学习器不能太差,要有一定的准确度;多样性则是个体学习器之间的输出要具有差异性。
通过下面的这三个例子可以很容易看出这一点,准确度较高,差异度也较高,可以较好地提升集成性能。

集成策略:如何结合多个基模型的预测结果,例如:
公式解析 $$ P(H(\boldsymbol{x}) \neq f(\boldsymbol{x})) = \sum_{k=0}^{\lfloor T/2 \rfloor} \binom{T}{k} (1-\epsilon)^k \epsilon^{T-k} \leq \exp\left(-\frac{1}{2} T (1 - 2\epsilon)^2\right) $$
1. 公式含义
2. 推导思路
两个基本结论
1. 收敛速率随个体学习器数量 T 指数下降
2. ϵ = 0.5 的个体学习器对收敛没有作用
根据个体学习器的生成方式,目前集成学习可分为两类,代表作如下:
Boosting是一种串行的工作机制,即个体学习器的训练存在依赖关系,必须一步一步序列化进行。
其基本思想是:增加前一个基学习器在训练过程中预测错误样本的权重,使得后续基学习器更加关注这些打标错误的训练样本,尽可能纠正这些错误,然后基于调整后的样本分布训练下一个基学习器,如此重复,一直向下串行直至产生需要的T个基学习器,Boosting最终对这T个学习器进行加权结合,产生学习器委员会。
Boosting族算法最著名、使用最为广泛的就是AdaBoost,因此下面主要是对AdaBoost算法进行介绍。
AdaBoost使用的是指数损失函数,因此AdaBoost的权值与样本分布的更新都是围绕着最小化指数损失函数进行的。
看到这里回想一下之前的机器学习算法,不难发现机器学习的大部分带参模型只是改变了最优化目标中的损失函数:如果是Square loss,那就是最小二乘了;如果是Hinge Loss,那就是著名的SVM了;如果是log-Loss,那就是Logistic Regression了。
$$ H(\boldsymbol{x}) = \sum_{t=1}^T \alpha_t h_t(\boldsymbol{x}) $$ ℓexp(H|𝒟) = 𝔼x ∼ 𝒟[e−f(x)H(x)]
1. 符号含义
2. 指数损失函数的意义
指数损失函数的形式为: ℓexp(H|𝒟) = 𝔼x ∼ 𝒟[e−f(x)H(x)] - 直观解释: - 当 H(x) 与 f(x) 同号时(预测正确),指数项 e−f(x)H(x) 接近 0,损失小。 - 当 H(x) 与 f(x) 异号时(预测错误),指数项趋近于正无穷,损失极大。 - 因此,该损失函数对错误样本的惩罚非常严格,迫使模型优先修正错误。
AdaBoost的目标是选择基学习器 ht 和权重 αt,使得集成模型 H(x) 能够最小化指数损失函数: $$ \min_{\alpha_1, h_1, \dots, \alpha_T, h_T} \mathbb{E}_{\boldsymbol{x} \sim \mathcal{D}} \left[ e^{-f(\boldsymbol{x}) \sum_{t=1}^T \alpha_t h_t(\boldsymbol{x})} \right] $$
优化策略
AdaBoost采用前向分步算法(Forward Stagewise Algorithm),逐轮迭代优化: 1. 初始化样本权重:初始时所有样本权重相等。 2. 训练基学习器 ht:在当前样本权重分布下,训练一个弱学习器 ht。 3. 计算权重 αt:根据 ht 的错误率 ϵt 计算其权重: $$ \alpha_t = \frac{1}{2} \ln \left( \frac{1 - \epsilon_t}{\epsilon_t} \right) $$ 4. 更新样本权重:提高被 ht 错分类样本的权重,降低正确分类样本的权重。 5. 重复步骤 2-4,直到训练完成 T 轮。
假设一个二分类任务,真实标签 f(x) ∈ {−1, +1},集成模型预测值 $H(\boldsymbol{x}) = \sum_{t=1}^T \alpha_t h_t(\boldsymbol{x})$: - 若 H(x) > 0,预测为 +1; - 若 H(x) < 0,预测为 −1。
此时,指数损失函数的值反映了模型对错误样本的惩罚程度: - 正确预测时,e−f(x)H(x) ≈ 0; - 错误预测时,e−f(x)H(x) ≫ 1。

在集成学习中,Boosting 算法的核心在于动态调整样本权重 ,以逐步聚焦难分类样本。Boosting 主要通过两种方法实现样本权重的更新:重赋权法(re-weighting) 和 重采样法(re-sampling) 。
重赋权法 : 对每个样本附加一个权重,这时涉及到样本属性与标签的计算,都需要乘上一个权值。 重采样法 : 对于一些无法接受带权样本的及学习算法,适合用“重采样法”进行处理。方法大致过程是,根据各个样本的权重,对训练数据进行重采样,初始时样本权重一样,每个样本被采样到的概率一致,每次从N个原始的训练样本中按照权重有放回采样N个样本作为训练集,然后计算训练集错误率,然后调整权重,重复采样,集成多个基学习器。
从偏差-方差分解来看:Boosting算法主要关注于降低偏差,每轮的迭代都关注于训练过程中预测错误的样本,因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成学习器。
任务分为分类,回归,聚类,降维等,而分类中还分为二分类和多分类
从AdaBoost的算法流程来看,标准的AdaBoost只适用于二分类问题。
通过改造AdaBoost对样本分类的限制和损失函数,可以实现多分类或回归问题,这样改造出来的算法框架成为Gradient Boosting
1. GBDT 的核心思想
GBDT 是基于梯度提升(Gradient Boosting)框架的集成学习方法,其特点包括: - 基学习器:使用CART(分类与回归树)作为个体学习器。 - 损失函数: - 回归问题:平方损失(Squared Loss): err(Ht(x), f(x)) = (Ht(x) − f(x))2 - 二分类问题:对数似然损失(Log-Likelihood Loss,类似逻辑回归): err(Ht(x), f(x)) = log (1 + exp (−f(x)Ht(x))) - 多分类问题:扩展为多分类对数损失。
2. XGBoost 的定位
XGBoost(eXtreme Gradient Boosting)是 GBDT 的一种高效实现和改进,类似于 LIBSVM 对 SVM 的优化关系。其核心目标是: - 提升训练速度:通过并行计算、内存优化等工程技巧。 - 增强模型性能:引入正则化项、缺失值处理、自适应学习率等改进。
XGBoost即eXtremeGradient Boosting的缩写,XGBoost与GBDT的关系可以类比为 LIBSVM和SVM的关系,即XGBoOst是GBDT的一种高效实现和改进。
它并非一个全新的算法框架,而是对标准 GBDT 进行了大量的工程优化和算法增强。

Bagging是一种并行式的集成学习方法,即基学习器的训练之间没有前后顺序可以同时进行
Bagging使用“有放回”采样的方式选取训练集,对于包含m个样本的训练集,进行m次有放回的随机采样操作,从而得到m个样本的采样集,这样训练集中有接近36.8%的样本没有被采到,可用作验证集来对泛化性能进行“包外估计”(out-of-bag estimate)。
按照相同的方式重复进行,我们就可以采集到T个包含m个样本的数据集,从而训练出T个基学习器,最终对这T个基学习器的输出进行结合。
Boosting算法一大特点是串行,这样诚然可以降低模型的偏差,增强拟合能力,但是当数据过大时,一大缺点就是会降低学习效率
Bagging作为并行式的集成学习方法,通过综合多个基学习器的结果,可以增加学习效率
二者差异性:
1.对目标的拟合程度:Boosting对目标有更好的拟合能力(偏差小);Bagging则偏差相对大一些
2.运行效率:由于并行的特点,Bagging的运行效率是大于Boosting的
3.泛化能力:由于Bagging每个学习器不会受其他学习器的影响,泛化能力(方差大)相对于Boosting
更好

可以看出Bagging主要通过样本的扰动来增加基学习器之间的多样性,因此Bagging的基学习器应为那些对训练集十分敏感的不稳定学习算法,例如:神经网络与决策树等。
从偏差-方差分解来看,Bagging算法主要关注于降低方差,即通过多次重复训练提高稳定性。
不同于AdaBoost的是,Bagging可以十分简单地移植到多分类、回归等问题。总的说起来则是:AdaBoost关注于降低偏差,而Bagging关注于降低方差。
在机器学习中,自助采样法(Bootstrap Sampling) 是 Bagging 算法的核心技术之一。其核心思想是从原始数据集中有放回地随机抽取样本,形成新的训练子集。这一过程的一个重要数学性质是:当样本量 n 趋近于无穷大时,每个样本在 Bootstrap 样本集中未被抽中的概率趋近于 $\frac{1}{e} \approx 36.6\%$。以下是详细解析:
1. 公式推导
假设我们从 n 个样本中有放回地抽取 n 次,形成一个 Bootstrap 样本集。对于任意一个特定样本(如第 i 个样本),它在某次抽样中未被选中的概率为: $$ 1 - \frac{1}{n} $$ 因此,它在整个 n 次抽样中从未被选中的概率为: $$ \left(1 - \frac{1}{n}\right)^n $$ 当 n → ∞ 时,该概率的极限为: $$ \lim_{n \to \infty} \left(1 - \frac{1}{n}\right)^n = \frac{1}{e} \approx 0.3679 \quad (\text{即 } 36.6\%) $$ 在每次 Bootstrap 采样中,约有 36.6% 的样本未被选中 ,这些样本称为 Out-of-Bag(OOB,包外估计)样本 。
2. OOB 样本的应用
在 Bagging 算法中,OOB 样本具有以下重要作用: 1.
无偏验证:
每个基学习器的训练数据不包含其对应的 OOB
样本,因此可以用这些样本直接评估模型性能(即 OOB
误差),无需额外的交叉验证。 2. 特征重要性评估:
在随机森林中,通过比较 OOB
样本在打乱某个特征后的预测误差变化,可以衡量该特征的重要性。
3. 与其他采样方法的对比
| 采样方法 | 是否放回 | 样本覆盖范围 | 典型应用场景 |
|---|---|---|---|
| Bootstrap 采样 | 是 | 约 63.4% 样本被重复使用 | Bagging、随机森林 |
| 简单随机采样 | 否 | 所有样本唯一出现 | 传统交叉验证 |
随机森林(Random Forest)是Bagging的一个拓展体,它的基学习器固定为决策树,多棵树也就组成了森林,而“随机”则在于选择划分属性的随机,随机森林在训练基学习器时,也采用有放回采样的方式添加样本扰动,同时它还引入了一种属性扰动,即在基决策树的训练过程中,在选择划分属性时,RF先从候选属性集中随机挑选出一个包含K个属性的子集,再从这个子集中选择最优划分属性 。
这样随机森林中基学习器的多样性不仅来自样本扰动,还来自属性扰动,从而进一步提升了基学习器之间的差异度。相比决策树的Bagging集成,随机森林的起始性能较差(由于属性扰动,基决策树的准确度有所下降),但随着基学习器数目的增多,随机森林往往会收敛到更低的泛化误差。同时不同于Bagging中决策树从所有属性集中选择最优划分属性,随机森林只在属性集的一个子集中选择划分属性,因此训练效率更高。
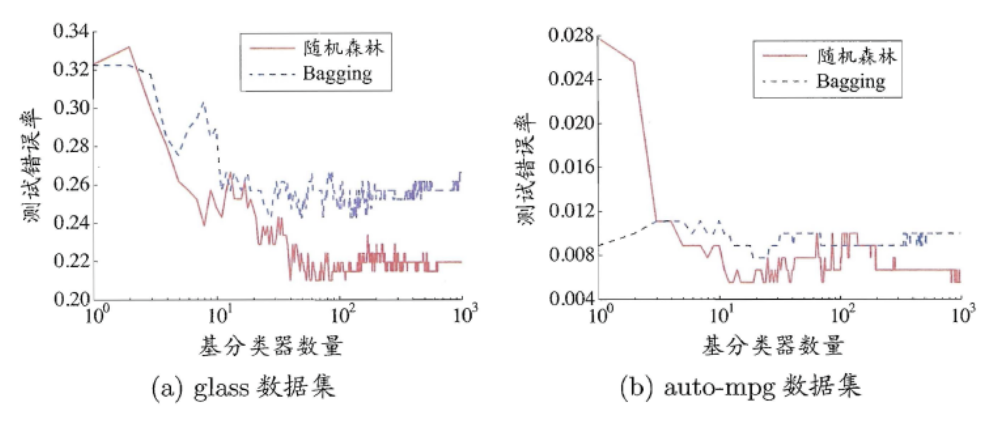
在集成学习中,结合策略是将多个基学习器的输出整合为最终预测结果的关键步骤。以下是针对回归和分类问题的不同结合策略及其核心要点:
定义:在训练好多个基学习器后,如何将其输出组合成集成模型的最终输出。
简单平均法(Simple Averaging)
加权平均法(Weighted Averaging)
绝对多数投票法(majority voting)提供了拒绝选项,这在可靠性要求很高的学习任务中是一个很好的机制。同时,对于分类任务,各个基学习器的输出值有两种类型,分别为类标记和类概率。

一些在产生类别标记的同时也生成置信度的学习器,置信度可转化为类概率使用,一般基于类概率进行结合往往比基于类标记进行结合的效果更好,需要注意的是对于异质集成,其类概率不能直接进行比较,此时需要将类概率转化为类标记输出,然后再投票。
学习法是一种更高级的结合策略,其核心思想是通过训练一个次级学习器(Meta-Learner) 来动态融合多个基学习器的输出。其中,Stacking(堆叠泛化) 是学习法的典型代表,它通过将基学习器的预测结果作为新特征,进一步训练一个次级模型,最终实现更优的泛化性能。
Stacking 的基本原理
步骤概述:
Stacking 的优势
Stacking 的实现细节
在集成学习中,多样性增强(Diversity Enhancement) 是提升模型性能的关键策略。通过引入多样性,可以降低基学习器之间的相关性,从而减少误差传递和过拟合风险。以下是四种常见的多样性增强方法及其核心要点:
1. 数据样本扰动(Data Perturbation)
原理:通过修改训练数据的分布或采样方式,使每个基学习器看到不同的数据子集。
实现方式:
- Bagging(如随机森林):
- 随机有放回地采样(Bootstrap),生成多个不同的训练集。
- 对输入扰动敏感的基学习器(如决策树、神经网络)效果显著。
- 示例:
- 决策树对数据扰动敏感,Bagging 可有效提升其泛化能力。
- 线性模型(如线性回归、SVM)对数据扰动不敏感,Bagging 效果有限。
2. 输入属性扰动(Input Attribute Perturbation)
原理:通过改变输入特征的表示或选择,增加基学习器间的差异。
实现方式:
-
特征子集采样:每次随机选择部分特征进行训练(如随机森林中的列扰动)。
- 特征变换:对特征进行缩放、旋转或加噪声等操作。
- 适用场景:
- 数据包含大量冗余属性时,可大幅加速训练并提升多样性。
- 对高维数据(如图像、文本)尤其有效。
3. 输出属性扰动(Output Attribute Perturbation)
原理:通过修改训练样本的标签,间接影响基学习器的学习过程。
实现方式:
-
随机翻转标签:对部分样本的标记进行随机更改(需谨慎使用,避免干扰模型)。
- Dropout(神经网络):
- 在训练过程中随机“关闭”部分神经元,强制网络学习更鲁棒的特征。
- 类似于对输出属性的随机扰动,可提升模型泛化能力。
4. 算法参数扰动(Algorithm Parameter Perturbation)
原理:通过调整基学习器的超参数,生成不同的模型行为。
实现方式:
集成学习中常见的两种方法是什么?请分别介绍它们的原理和特点。集成学习相比于单个模型有什么优势和应用场景?
集成学习常见方法、原理、特点及优势
常见方法:Bagging 和 Boosting
原理与特点:
| 方法 | 原理 | 特点 |
|---|---|---|
| Bagging | 1. 自助采样:从训练集有放回抽取多个子集 2. 并行训练基模型 3. 聚合预测(投票/平均) |
- 降低方差 - 适合高方差模型(如未剪枝决策树) - 并行化,训练快 - 代表:随机森林 |
| Boosting | 1. 顺序训练:后一个模型修正前一个模型的错误 2. 加权困难样本 3. 加权组合模型 |
- 降低偏差 - 需弱学习器(如树桩) - 易过拟合(需正则化) - 代表:AdaBoost, GBDT, XGBoost |
集成学习的优势:
-
提升泛化能力:降低过拟合(Bagging)或欠拟合(Boosting)风险
- 增强鲁棒性:减少异常值/噪声影响(如投票机制)
- 突破性能上限:组合多个弱模型达到强模型效果
应用场景:
- 分类任务:医疗诊断(整合多模型减少误诊)
- 回归任务:房价预测(融合不同树模型提升精度)
- 不平衡数据:Boosting 加权少数类样本
- 高维数据:随机森林自动特征选择
如果在完全相同的训练集上训练了五个不同的模型,并且它们都达到了95%的准确率,是否还有机会通过结合这些模型来获得更好的结果?如果可以,该怎么做?如果不行,为什么?
模型结合提升性能的可能性与方法
是否可能提升:是,但需满足条件:模型错误不相关(即犯错样本不同)。
如何实现:
若无法提升的情况:
-
原因:模型高度相关(如相同算法、相同特征、相同超参)
- 数学解释:误差相关性 rho ≈ 1
时,集成误差 ≈单一模型误差
是否可以通过在多个服务器上并行来加速随机森林的训练?AdaBoost集成呢?为什么?
| 算法 | 是否支持并行 | 原因 |
|---|---|---|
| 随机森林 | ✅ 是 | 1. 树之间独立训练 2. 可分布式分配Bootstrap样本到不同服务器 3. 特征分裂也可并行(如选特征子集) |
| AdaBoost | ❌ 否 | 1.
模型必须顺序训练:后一个模型依赖前一个模型的样本权重更新 2. 无法解耦迭代过程 |
我们之前学习的分类/回归任务都属于 有监督学习 需要我们提供样本与标签
而马上要学习的聚类任务和后续学习的降维则属于 无监督学习 仅需提供样本
聚类是一种经典的无监督学习(unsupervised learning)方法,无监督学习的目标是通过对无标记训练样本的学习,发掘和揭示数据集本身潜在的结构与规律,即不依赖于训练数据集的类标记信息。
聚类试图将数据集中的样本划分为若干个通常是不相交的子集,每个子集称为一个“簇”( cluster)。通过这样的划分,每簇可能对应于一些潜在的概念(类别),如“浅色瓜”“深色瓜”,“有籽瓜”“无籽瓜”,甚至“本地瓜”“外地瓜”等;需说明的是,这些概念对聚类算法而言事先是未知的,聚类过程仅能自动形成簇结构, 簇所对应的概念语义需由使用者来把握和命名。
直观上来说,聚类是将相似的样本聚在一起,从而形成一个类簇(cluster)。涉及两个问题
明可夫斯基距离(Minkowski Distance)
明可夫斯基距离是一组常用的连续型距离度量,通过调整参数 $ p $ 可以统一表示多种距离形式,是欧氏距离和曼哈顿距离的推广。
1. 公式定义
对于两个 $ n $ 维向量 $ i = (x{i1}, x_{i2}, , x_{in}) $ 和 $ j = (x{j1}, x_{j2}, , x_{jn}) ,明可夫斯基距离的计算公式为:$ {}(i, j) = ( {u=1}^{n} |x{iu} - x{ju}|^p )^{} $$ 其中,$ p $ 是一个可调节的参数。
2. 特殊情况
3. 参数 $ p $ 的影响
我们知道属性分为两种:连续属性(continuous attribute)和离散属性(catergorical attribute有限个取值)。对于连续值的属性,一般都可以被学习器所用,有时会根据具体的情形作相应的预处理,例如:归一化等;而对于离散值的属性,需要作下面进一步的处理:
若属性值之间存在序关系(ordinal attribute),则可以将其转化为连续值,例如:身高属性“高”“中等”“矮”,可转化为{1, 0.5, 0}。
若属性值之间不存在序关系(non-ordinal attribute),则通常将其转化为向量的形式,例如:性别属性“男”“女”,可转化为{(1,0),(0,1)}。
连续属性和存在序关系的离散属性都可以直接参与计算,而不存在序关系的无序属性,我们一般采用VDM(Value Difference Metric)进行距离的计算
VDM 是一种专门用于离散无序属性的距离度量方法,通过统计信息量化不同类别间的差异。其核心思想是:若两个类别的样本在目标变量上的分布差异越大,则它们的距离越大。
1. 公式解析 $$
\text{VDM}_p(a, b) = \sum_{i=1}^{k} \left| \frac{m_{u,a,i}}{m_{u,a}} -
\frac{m_{u,b,i}}{m_{u,b}} \right|^p
$$ - 符号含义:
- $ a, b $:两个不同的类别值(如性别“男”和“女”)。
- $ m_{u,a,i} $:在属性 $ u $ 的第 $ i $ 个取值下,类别 $ a $
的样本数量。
- $ m_{u,a} $:类别 $ a $ 的总样本数量。
- $ k $:属性 $ u $ 的不同取值数目(如颜色属性有红、蓝、绿三种取值,则 $
k=3 $)。
- $ p $:距离幂指数(通常取 $ p=1 $ 或 $ p=2 $)。
2. 核心思想
3. 示例说明
假设我们有一个“颜色”属性(红、蓝、绿),目标变量是“是否购买商品”(0/1)。统计结果如下:
| 颜色 | 购买(1) | 不购买(0) | 总计 |
|---|---|---|---|
| 红 | 10 | 5 | 15 |
| 蓝 | 8 | 12 | 20 |
| 绿 | 3 | 7 | 10 |
计算“红”与“蓝”之间的 VDM 距离($ p=1 ):1.计算每个颜色在购买/不购买的比例: − 红:
P(1) = 10/15 , P(0) = 5/15 $
- 蓝:$ P(1) = 8/20 = 0.4 , P(0) =
12/20 = 0.6 $
2. 计算差异并求和:
VDM1(红, 蓝) = |0.67 − 0.4|+|0.33 − 0.6| = 0.27 + 0.27 = 0.54
于聚类算法不依赖于样本的真实类标,就不能像监督学习的分类那般,通过计算分对分错(即精确度或错误率)来评价学习器的好坏或作为学习过程中的优化目标。
直观上看,我们希望“物以类聚”,即同一簇的样本尽可能彼此相似,不同簇的样本尽可能不同换言之,聚类结果的“簇内相似度”( intra-cluster similarity)高且“簇间相似度” inter-cluster similarity)低
聚类性能度量有两类
1.基本概念

显然,$ a + b + c + d = $ 。
2. 常用外部指标
(1)Jaccard系数(JC) $$
\text{JC} = \frac{a}{a + b + c}
$$ -
含义:衡量两个划分的重叠程度,仅考虑正确匹配($ a )与矛盾情况(
b + c )。 − * * 范围 * *: [0,
1] $,值越大越好。
- 特点:对称性差,对噪声敏感 。
(2)Fowlkes-Mallows指数(FMI) $$
\text{FMI} = \sqrt{\frac{a}{a + b} \cdot \frac{a}{a + c}}
$$ - 含义:结合查准率($ )和查全率(
),反映正确匹配的综合能力。 − * * 范围 * *:
[0, 1] $,值越大越好。
- 特点:平衡性较好,适合小样本 。
(3)Rand指数(RI) $$
\text{RI} = \frac{2(a + d)}{m(m - 1)}
$$ - 含义:同时考虑正确匹配($ a + d )与总样本对数,适用于大规模数据。 − * * 范围 * *:
[0, 1] $,值越大越好。
- 特点:计算简单,但对噪声较鲁棒 。
常用指标
优点
局限性
3. 应用示例
假设一个包含4个样本的数据集,参考标签为 {A, A, B, B},聚类结果为
{C, C, D, D}:
- 计算样本对:
- $ a = 2 $(样本1-2同簇,参考与聚类均同类)。
- $ b = 0 $(参考同类但聚类不同类)。
- $ c = 0 $(参考不同类但聚类同类)。
- $ d = 2 $(参考不同类且聚类不同类)。
- 指标结果:
- JC = $ = 1 $(完美匹配)。
- FMI = $ = 1 $。
- RI = $ = $。
内部指标不依赖任何外部参考模型,直接通过簇内紧凑性和簇间分离性评估聚类结果。其核心思想是:
- 簇内高内聚:同一簇的样本尽可能相似(距离小)。
- 簇间低耦合:不同簇的样本尽可能不同(距离大)。
1. 基本定义
设聚类结果为 $ C = {C_1, C_2, , C_k} $,定义以下四个关键距离:
(1)簇内平均距离(avg(C)) $$
\text{avg}(C) = \frac{2}{|C|(|C| - 1)} \sum_{1 \leq i < j \leq |C|}
\text{dist}(\boldsymbol{x}_i, \boldsymbol{x}_j)
$$ - 含义:簇内所有样本对的平均距离。
- 目标:越小越好,表示簇内样本更紧密。
(2)簇内最大距离(diam(C)) diam(C) = max1 ≤ i < j ≤ |C|dist(xi, xj)
- 含义:簇内最远的两个样本之间的距离。
- 目标:越小越好,避免簇内存在离群点。
**(3)簇间最小距离($ d_{}(C_i, C_j) ) * *$ d_{}(C_i, C_j) = _{_i C_i, _j C_j}
(_i, _j) $$ - 含义:簇 $ C_i $ 和 $ C_j $
之间最近的两个样本的距离。
- 目标:越大越好,表示簇间分离度高。
**(4)簇中心距离($ d_{}(C_i, C_j) ) * *$ d_{}(C_i, C_j) = (_i, _j) $$ -
含义:簇 $ C_i $ 和 $ C_j $
的中心点(均值向量)之间的距离。
- 目标:越大越好,表示簇中心相隔较远。
2. 常用内部指标
1. DB指数(Davies-Bouldin Index, DBI)
2. Dunn指数(Dunn Index, DI)
3. 轮廓系数(Silhouette Coefficient)
单一样本的轮廓系数:
$$
s = \frac{b - a}{\max(a, b)}
$$
整体轮廓系数:所有样本轮廓系数的平均值。
示例:
若某样本 $ a = 2 , b = 5 $,则 $ s = =
0.6 $,表明该样本分类合理。
4.肘部法则(Elbow Method)
肘部法则是一种经验性方法,常用于确定K-means等聚类算法的最优簇数($ K $)。其核心思想是通过观察误差平方和(SSE, Sum of Squared Errors)随 $ K $ 值变化的趋势,寻找“肘部点”(即 SSE 下降速度明显减缓的拐点),从而选择最优的 $ K $ 值
SSE(误差平方和):衡量每个样本到其所属簇中心的距离平方和,公式为: $$ \text{SSE} = \sum_{i=1}^n \|x_i - \mu_{c_i}\|^2 $$ 其中 $ x_i $ 是样本点,$ _{c_i} $ 是其所属簇中心。
趋势分析:
肘部点的意义:
肘部点对应的 $ K $
值是模型复杂度(簇数)与聚类效果(SSE)之间的平衡点。
指标对比与选择
| 指标 | 计算方式 | 目标 | 适用场景 | 局限性 |
|---|---|---|---|---|
| DBI | 簇内平均距离与簇中心距离的比值 | 越小越好 | 球形簇,需指定 $ k $ | 对离群点敏感 |
| Dunn指数 | 簇间最小距离与簇内最大直径的比值 | 越大越好 | 强调簇间分离与簇内紧凑 | 计算复杂,受离群点影响 |
| 轮廓系数 | 样本到同簇/异簇的平均距离差 | 越接近 1 越好 | 快速评估,适合 K-Means | 对非球形簇不敏感 |
原型聚类即“基于原型的聚类”(prototype-based clustering),原型表示模板的意思,就是通过参考一个模板向量或模板分布的方式来完成聚类的过程,通常情形下算法先对原型进行初始化,然后对原型进行迭代更新求解。采用不同的原型表、不同的求解方式,将产生不同的算法。
常见的K-Means便是基于簇中心(原型向量)来实现聚类,混合高斯聚类则是基于簇分布(概率模型)来实现聚类。
目标函数:最小化所有样本到其所属簇中心的平方距离之和:
$$
E = \sum_{i=1}^{k} \sum_{\boldsymbol{x} \in C_i} \|\boldsymbol{x} -
\boldsymbol{\mu}_i\|_2^2
$$ 其中,$ i = { C_i} $ 是簇 $ C_i $ 的均值向量。
算法步骤
如何选择 $ k $ 值?

此法相对于 K-means 做出了一个小的改进。在一开始选择 k 个聚类中心时,并不是随机初始化 k 个,而是首先随机出 1 个,然后循环 k−1k−1 次选择剩下的 k-1 个聚类中心。选择的规则是:每次选择最不可能成为新的聚类中心的样本,或者是到所有聚类中心的最小距离最大的样本。
避免不良初始化 :传统K-means随机初始化可能导致中心过于集中,而K-means++通过“最大化最小距离”策略,使初始中心分布更均匀。
此法叫做二分 K-means 算法。具体的,在一开始将所有的样本划分为一个簇,然后每次选择一个误差最大的簇进行二分裂,不断分裂直到收敛。这种方法不能使得 Loss 最小,但是可以作为 K-means 算法的一个预热,比如可以通过这种方法得到一个相对合理的簇中心,然后再利用 K-means 算法进行聚类。
降低计算复杂度 :每次仅对一个簇进行二分,时间复杂度为 O(k⋅m⋅n) ,适合大规模数据。
提供合理初始中心 :可作为传统K-means的预处理,减少随机初始化的影响。
核心思想:
LVQ
是一种有监督的原型聚类算法,结合了神经网络与向量量化技术。它通过维护一组原型向量(Prototype
Vectors)来代表不同类别,并利用这些原型对数据进行分类或聚类。与 K-Means
类似,LVQ
会为每个簇分配一个原型向量,但其更新规则受类别标签的指导,因此更适用于分类任务
。
算法特点:
一句话概述算法:高斯混合聚类算法是一种概率模型,假设数据由多个高斯分布混合而成,通过迭代优化参数以拟合数据分布,常用于无监督学习中的聚类任务。
算法过程:
初始化参数: 随机初始化每个分量的均值、协方差矩阵和混合系数。
E 步(Expectation): 对每个数据点,计算它属于每个分量的后验概率,即计算每个分量的权重。
M 步(Maximization): 使用E步计算得到的后验概率,更新每个分量的均值、协方差矩阵和混合系数。
迭代: 重复执行E步和M步,直到模型参数收敛或达到预定的迭代次数。
GMM的优点包括对各种形状和方向的聚类簇建模能力,以及对数据分布的灵活性。它在许多领域,如模式识别、图像处理和自然语言处理等,都有广泛的应用。

以下是高斯混合聚类(GMM)算法的详细步骤及EM算法中E步与M步的解释:
算法流程解析
输入:样本集 $ D = {x_1, x_2, , x_m} $,混合成分个数
$ k $。
输出:簇划分 $ C = {C_1, C_2, , C_k} $。
步骤详解
初始化模型参数
随机初始化或通过K-means初步估计以下参数:
迭代优化参数(EM循环)
重复以下步骤直到收敛(如对数似然变化小于阈值):
E步(期望步):
对每个样本 $ x_j $,计算其由第 $ i $
个高斯分布生成的后验概率(责任度 $ {ji} ):$ {ji} = p(z_j = i | x_j) = $$ 其中
$ (x | , ) $ 是高斯分布的概率密度函数。
M步(最大化步):
根据当前的责任度 $ _{ji} $,更新模型参数:
簇划分
E步与M步的核心作用
E步(期望步)
M步(最大化步)
西瓜书读书笔记整理(九) —— 第九章 聚类_西瓜书笔记第9章-CSDN博客
若样本分布为同心的两个环,kmeans则无法做到良好的聚类效果,因此引出密度聚类
密度聚类是一种基于样本分布密集程度的无监督学习方法,其核心思想是:将高密度区域划分为同一簇,低密度区域视为噪声或边界。
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是密度聚类的典型代表,通过两个关键参数 $ $ 和 $ MinPts $ 描述样本分布的紧密性。
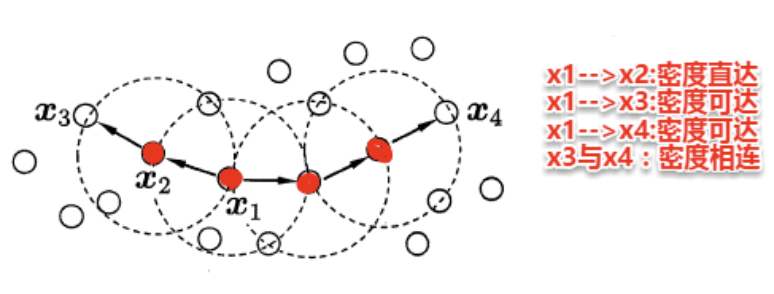
DBSCN定义的簇
简单来理解DBSCAN:找出一个核心对象所有密度可达的样本集合形成簇。首先从数据集中任选一个核心对象A,找出所有A密度可达的样本集合,将这些样本形成一个密度相连的类簇,直到所有的核心对象都遍历完。DBSCAN算法的流程如下图所示:

层次聚类是一种通过构建树状结构(Dendrogram)将数据划分为不同层次的聚类方法。其核心思想是:
-
凝聚型(Agglomerative):从每个样本作为一个独立簇开始,逐步合并最相似的簇,直到达到预设的簇数或形成一个唯一簇。
-
分裂型(Divisive):与凝聚型相反,从整个数据集作为一个簇开始,逐步分裂为更小的簇。
本节重点介绍AGNES(Agglomerative Nesting),一种经典的自底向上的层次聚类算法。
AGNES 的关键在于如何定义簇间距离,常见的三种方法如下:
(1)最小距离(Single Linkage) dmin(Ci, Cj) = minx ∈ Ci, z ∈ Cjdist(x, z) - 含义:两个簇之间最近的两个样本的距离。
(2)最大距离(Complete Linkage) dmax(Ci, Cj) = maxx ∈ Ci, z ∈ Cjdist(x, z) - 含义:两个簇之间最远的两个样本的距离。
(3)平均距离(Average Linkage) $$ d_{\text{avg}}(C_i, C_j) = \frac{1}{|C_i| |C_j|} \sum_{\boldsymbol{x} \in C_i} \sum_{\boldsymbol{z} \in C_j} \text{dist}(\boldsymbol{x}, \boldsymbol{z}) $$ - 含义:两个簇所有样本对距离的平均值。

假设任务是将下面8个点聚类成3个簇:A1(2,10), A2(2,5), A3(8,4), B1(5,8), B2(7,5), B3(6,4), C1(1,2), C3(4,9),距离函数是欧式距离。假设初始选择A1,B1,C1分别作为每个聚类的中心,用Kmeans算法给出计算过程。


Kmeans初始类簇中心如何选取?K值如何确定?请简要阐述。
一、初始类簇中心的选取 (如何选好的起始点?)
传统K-means随机选择初始中心点,容易导致结果不稳定(多次运行结果不同)或陷入局部最优(效果差)。改进方法主要有:
二、K值(簇数量)的确定 (如何知道分几类?)
K值通常需要预先指定,但没有绝对正确的答案。常用方法基于评估不同K值下聚类结果的“质量”,寻找拐点或最优值:
K值 - SSE曲线图。观察曲线,寻找SSE下降幅度突然变得平缓的那个K值(形如手臂的“肘关节”)。a)和与其他簇的分离度(b)。a(i) = i
到同簇内所有其他点的平均距离(簇内不相似度)。b(i) = i
到所有其他簇中点的平均距离的最小值(最近邻簇的不相似度)。s(i) = (b(i) - a(i)) / max(a(i), b(i))。值在[-1,
1]之间。k近邻算法简称kNN(k-Nearest Neighbor),是一种经典的监督学习方法,是数据挖掘十大算法之一。其工作机制十分简单:给定某个测试样本,kNN基于某种距离度量在训练集中找出与其距离最近的k个带有真实标记的训练样本,然后基于这k个邻居的真实标记来进行预测,类似于集成学习中的基学习器结合策略:分类任务采用投票法,回归任务则采用平均法。
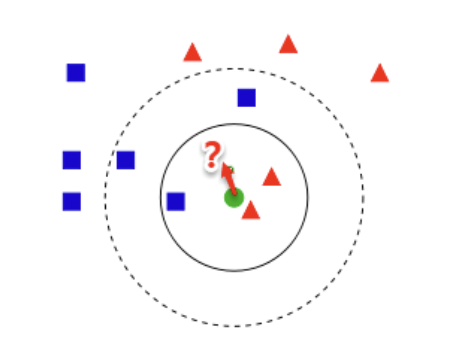
核心思想
1NN 分类器通过将测试样本 $ $ 分配到其最近邻样本 $ $
的类别来完成预测。其错误概率取决于两个关键因素: - $ $
的真实类别:$ P(c | ) $,即给定 $ $ 属于类别 $ c $
的概率。
- $ $ 的类别:$ P(c | ) $,即 $ $ 属于类别 $ c $
的概率。
错误概率公式
若测试样本 $ $ 的最近邻为 $ ,则1NN分类器出错的概率为:$
P() = 1 - P() = 1 - _{c } P(c | ) P(c | ) $$ 其中: - $ $
是所有可能的类别集合。
- $ P(c | ) : $ 属于类别 $ c $
的条件概率。
- $ P(c | ) : $ 属于类别 $ c $
的条件概率。
通过证明可以发现一个令人震惊的结论:最近邻分类器的错误率不超过贝叶斯最优分类器错误率的两倍。
对于距离度量,不同的度量方法得到的k个近邻不尽相同,从而对最终的投票结果产生了影响,因此选择一个合适的距离度量方法也十分重要。
在上一篇聚类算法中,在度量样本相似性时介绍了常用的几种距离计算方法,包括闵可夫斯基距离,曼哈顿距离,VDM等。在实际应用中,kNN的距离度量函数一般根据样本的特性来选择合适的距离度量,同时应对数据进行去量纲/归一化处理来消除大量纲属性的强权政治影响。
使用knn的前提是样本空间的密度要一定大,但是这个条件在现实中很难满足,因此引出降维操作
kNN的重要假设: 任意测试样本 附近任意小的 距离范围内总能找到一个训练样本,即训练样本的采样密度足够大,或称为 “密采样”( dense sample) 。然而,这个假设在现实任务中通常很难满足
样本的特征数也称为维数(dimensionality),当维数非常大时,也就是通常所说的“维数灾难”(curse of dimensionality),具体表现在:在高维情形下,数据样本变得十分稀疏,因为此时要满足训练样本为“密采样”的总体样本数目是一个触不可及的天文数字。训练样本的稀疏使得其代表总体分布的能力大大减弱,从而消减了学习器的泛化能力;同时当维数很高时,计算距离也变得十分复杂,甚至连计算内积都不再容易
缓解维数灾难的一个重要途径就是降维(dimension reduction),即通过某种数学变换将原始高维空间转变到一个低维的子空间。在这个子空间中,样本的密度将大幅提高,同时距离计算也变得容易。这
时也许会有疑问,降维之后不是会丢失原始数据的一部分信息吗?
实际上,在很多实际问题中,虽然训练数据是高维的,但是与学习任务相关也许仅仅是其中的一个低维子空间,也称为一个低维嵌入,例如:数据属性中存在噪声属性、相似属性或冗余属性等,对高维数据进行降维能在一定程度上达到提炼低维优质属性或降噪的效果。
MDS(Multidimensional Scaling,多维尺度分析)是一种经典的降维技术,其核心目标是将高维数据映射到低维空间(如二维或三维),同时尽可能保留原始数据中样本点之间的距离关系。以下是其核心原理与应用要点:
1. 核心思想
2. 算法步骤
MDS 的核心是通过矩阵分解从距离矩阵推导低维坐标: 1.
构建距离矩阵 $ D $:
对于 $ r $ 个样本,计算两两之间的距离,形成 $ r r $ 的矩阵 $ D $,其中 $
D_{ij} $ 表示样本 $ i $ 和 $ j $ 的距离 。
双中心化(Double Centering):
构造矩阵 $ B = - H D^{(2)} H $,其中 $ D^{(2)} $ 是距离的平方矩阵,$ H =
I - ^$ 是中心化矩阵 。
特征值分解:
对 $ B $ 进行特征值分解,得到 $ B = V V^$,其中 $ $
是按降序排列的特征值对角矩阵,$ V $ 是对应的特征向量矩阵 。
构造低维坐标:
选择前 $ d’ $ 个最大特征值($ d’ $
为目标维度)和对应的特征向量,计算低维坐标矩阵:
Z = Λ1/2V⊤
其中 $ ^{1/2} $ 是特征值矩阵的平方根 。
3. 关键特性
线性降维通过线性变换将高维数据 $ ^{d m} $ 投影到低维空间 $ ^{d’ m} ( d’ d ),保留数据的主要信息。其数学表达为:$ = ^ $$
变换矩阵 $ ^{d d’} $:
每一列是正交的基向量,构成低维子空间的坐标系。
目标:选择 $ $ 使得低维表示 $ $ 最大化保留原始数据的信息(如方差、距离等)。
MDS:
直接以保留高维空间中样本点之间的距离关系为目标。降维后的低维空间需尽可能保持原始样本两两之间的距离(如欧氏距离、自定义相似性距离)。
其他线性方法(如PCA、LDA):
不同于MDS采用距离保持的方法,主成分分析(Principal Component Analysis ,PCA)是一种经典的无监督降维算法 ,其核心目标是通过线性变换将高维数据映射到低维空间,同时保留数据的最大方差信息 (即信息损失最小)
直接通过一个线性变换,将原始空间中的样本投影到新的低维空间中。
简单来理解这一过程便是:PCA采用一组新的基(向量)来表示样本点,其中每一个基向量都是原始空间基向量的线性组合,通过使用尽可能少的新基向量来表出样本,从而达到降维的目的。
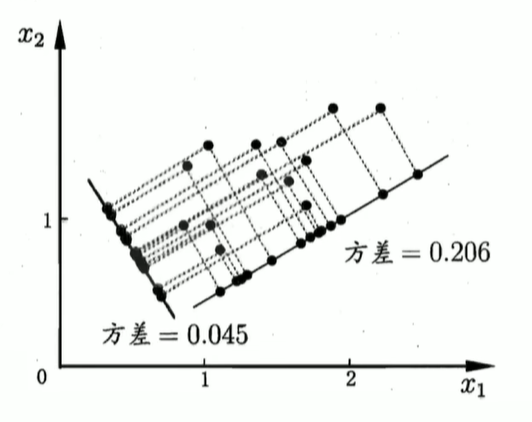
假设使用d’个新基向量来表示原来样本,实质上是将样本投影到一个由d’个基向量确定的一个超平面上(即舍弃了一些维度),要用一个超平面对空间中所有高维样本进行恰当的表达,最理想的情形是:若这些样本点都能在超平面上表出且这些表出在超平面上都能够很好地分散开来。但是一般使用较原空间低一些维度的超平面来做到这两点十分不容易,因此我们退一步海阔天空,要求这个超平面应具有如下两个性质:
最近重构性:样本点到超平面的距离足够近,即尽可能在超平面附近;
最大可分性:样本点在超平面上的投影尽可能地分散开来,即投影后的坐标具有区分性。
这里十分神奇的是:最近重构性与最大可分性虽然从不同的出发点来定义优化问题中的目标函数,但最终这两种特性得到了完全相同的优化问题:

若数据已中心化(均值为零),则 $ ^$ 是样本协方差矩阵的 $ m $ 倍。此时,PCA的优化问题转化为: $$ \begin{aligned} & \underset{\mathbf{W}}{\text{maximize}} & & \text{tr}\left( \mathbf{W}^\top \mathbf{X} \mathbf{X}^\top \mathbf{W} \right) \\ & \text{subject to} & & \mathbf{W}^\top \mathbf{W} = \mathbf{I} \end{aligned} $$ 通过拉格朗日乘数法,该问题的解为 $ ^$ 的前 $ d’ $ 个最大特征值对应的特征向量
优化目标:
maxW tr(W⊤XX⊤W) s.t. W⊤W = I
其中,$ ^{d m} $ 是中心化后的数据矩阵(均值为零)。
拉格朗日乘数法:
引入拉格朗日乘子 $ ,构造拉格朗日函数:$
(, ) = ( ^ ^ ) - ( (^ - ) ) $$
对 $ \mathbf{W} $ 求导并令导数为零,得到:
$$ ^ = $$
即 $ \mathbf{X} \mathbf{X}^\top $ 的特征向量 $ \mathbf{w}_i $ 满足:
$$ ^_i = _i _i $$
1. 核心问题
在PCA中,我们希望找到一个 $ d’ d $ 的变换矩阵 $ $,其列向量是协方差矩阵 $ ^$ 的特征向量,且满足正交约束 $ ^ = $。关键问题是:如何从 $ d $ 个特征向量中选择 $ d’ $ 个最优的?
2. 数学推导
特征值分解:
协方差矩阵 $ {d d} $ 可分解为: XX⊤W = WΛ
其中,$ = (_1, _2, , _d) $ 是特征值对角矩阵,$ $
是特征向量矩阵。
优化目标转化:
PCA的目标是最大化 $ (^ ^) 。利用特征值分解,可得:$
^ ^ = ^( ) = 因此,优化目标变为:
{} () = {i=1}^{d’} _i $$ 即选择 $ d’ $ 个最大的特征值 $ _i $
对应的特征向量组成 $ $。
3. 特征向量选择策略

待学习
流形学习(manifold learning)是一种借助拓扑流形概念的降维方法,流形是指在局部与欧式空间同胚的空间,即在局部与欧式空间具有相同的性质,能用欧氏距离计算样本之间的距离。这样即使高维空间的分布十分复杂,但是在局部上依然满足欧式空间的性质,基于流形学习的降维正是这种 “邻域保持” 的思想。其中 等度量映射(Isomap)试图在降维前后保持邻域内样本之间的距离,而局部线性嵌入(LLE)则是保持邻域内样本之间的线性关系 。
等度量映射的基本出发点是:高维空间中的直线距离具有误导性,因为有时高维空间中的直线距离在低维空间中是不可达的。因此利用流形在局部上与欧式空间同胚的性质,可以使用近邻距离来逼近测地线距离,即对于一个样本点,它与近邻内的样本点之间是可达的,且距离使用欧式距离计算,这样整个样本空间就形成了一张近邻图,高维空间中两个样本之间的距离就转为最短路径问题。可采用著名的Dijkstra算法或Floyd算法计算最短距离,得到高维空间中任意两点之间的距离后便可以使用 MDS 算法来其计算低维空间中的坐标。
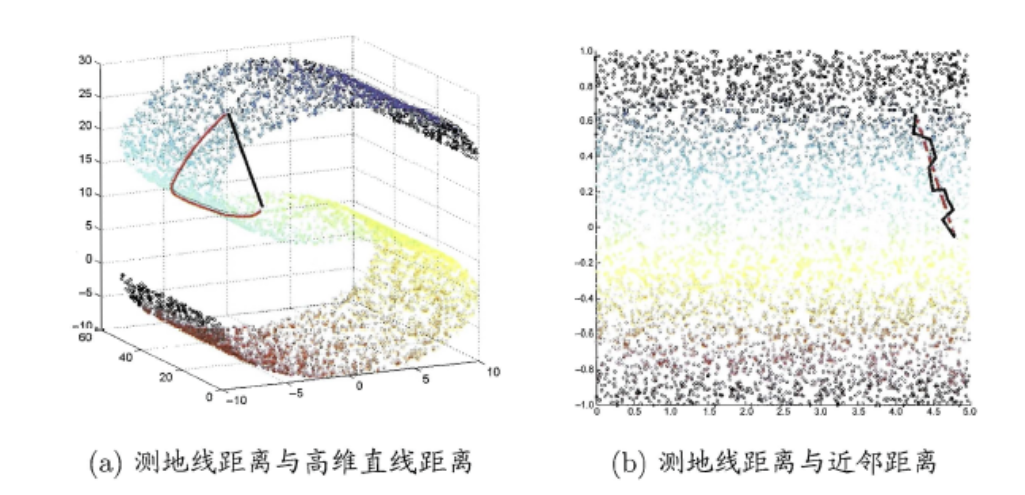
Isomap算法流程如下图:

对于近邻图的构建,常用的有两种方法:一种是指定近邻点个数,像kNN一样选取k个最近的邻居;另一种是指定邻域半径,距离小于该阈值的被认为是它的近邻点。但两种方法均会出现下面的问题:
若邻域范围指定过大,则会造成“短路问题”,即本身距离很远却成了近邻,将距离近的那些样本扼杀在摇篮。
若邻域范围指定过小,则会造成“断路问题”,即有些样本点无法可达了,整个世界村被划分为互不可达的小部落。
待学习
1. 核心思想
度量学习(Metric Learning)的核心目标是学习一个合理的距离度量,使得相似样本距离更近,不相似样本距离更远。传统欧式距离(Euclidean Distance)虽然简单,但其固定权重无法反映不同特征的实际重要性。因此,我们引入加权欧式距离,通过可调节的参数(权重)优化距离计算。
2. 欧式距离与加权欧式距离
标准欧式距离:
$$
\text{dist}_{\text{ed}}^2(\boldsymbol{x}_i, \boldsymbol{x}_j) =
\|\boldsymbol{x}_i - \boldsymbol{x}_j\|_2^2 = \sum_{k=1}^d
(\boldsymbol{x}_{i,k} - \boldsymbol{x}_{j,k})^2
$$
每个特征维度对距离的贡献相同,未考虑特征的重要性差异。
加权欧式距离:
distwed2(xi, xj) = (xi − xj)⊤W(xi − xj)
其中,$ = () $ 是对角权重矩阵,$ w_k $ 表示第 $ k $ 个特征的权重。
展开后为: $$
\text{dist}_{\text{wed}}^2(\boldsymbol{x}_i, \boldsymbol{x}_j) =
\sum_{k=1}^d w_k (\boldsymbol{x}_{i,k} - \boldsymbol{x}_{j,k})^2
$$
3. 权重的作用
4. 度量学习的目标
通过学习最优权重 $ ,使以下目标成立: − * * 相似样本 * *:加权距离小( _{}^2(_i, j) )。 − * * 不相似样本 * *:加权距离大( {}^2(_i, _j) $)。
典型优化问题形式: minw ∑(xi, xj) ∈ Sdistwed2(xi, xj) + λ∥w∥22 其中,$ S $ 是相似样本对集合,$ $ 是正则化项防止过拟合。
总结来说,
- 降维是将原高维空间嵌入到一个合适的低维子空间中,接着在低维空间中进行学习任务
- 度量学习则是试图去学习出一个 *距离度量* 来等效降维的效果
1. 核心思想
LMNN 是一种监督度量学习方法,其目标是通过学习一个线性变换矩阵 $ $,使同类样本在变换后的空间中更紧密,不同类样本被推开,从而提升KNN等基于距离的算法性能。其核心是引入最大边距(Large Margin)的概念,类似于SVM的分类边界。
2. 损失函数
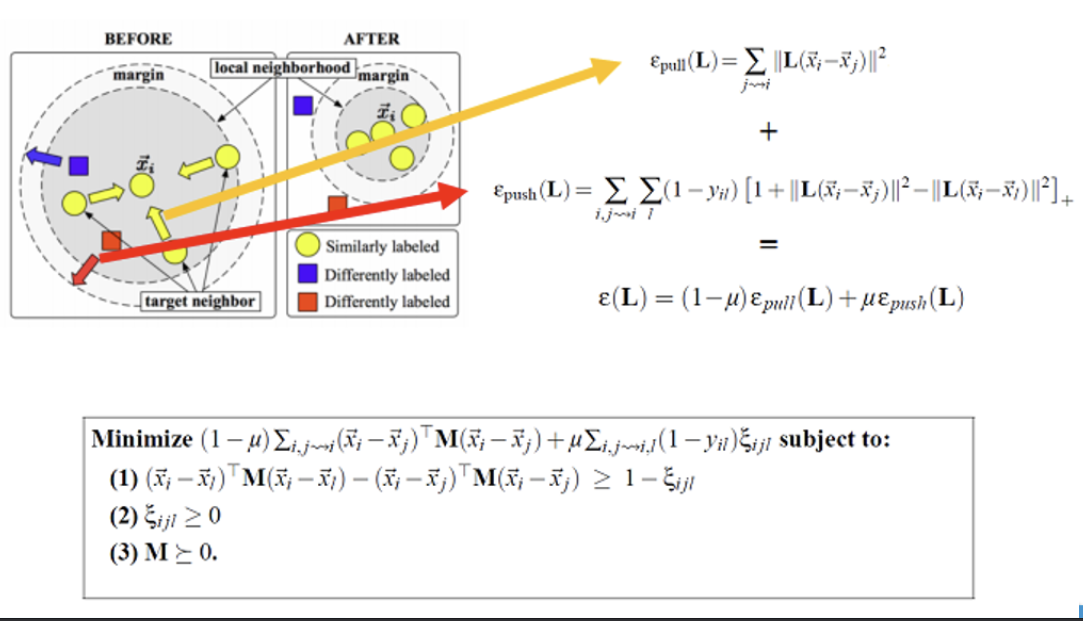
LMNN 的优化目标由两部分组成: - Pull
Loss(拉力损失):
使同类样本对的距离尽可能小,公式为: $$
\varepsilon_{\text{pull}}(\mathbf{L}) = \sum_{j \sim i}
\|\mathbf{L}(\bar{\boldsymbol{x}}_i - \bar{\boldsymbol{x}}_j)\|^2
$$ 其中,$ j i $ 表示与样本 $ i $ 同类的最近邻样本。
Push Loss(推力损失):
使不同类样本对的距离至少保持一个固定边距 $ {ijl} ,公式为:$
{}() = {i,j,l} (1 - y{il}) + $$ 其中,$ y{il} = 1
$ 表示样本 $ i $ 和 $ l $ 属于同一类,否则为0;$ []_+ $
表示取正值部分。
总损失函数:
ε(L) = (1 − μ)εpull(L) + μεpush(L)
参数 $ $ 控制两类损失的权重。
3. 优化问题
LMNN 的目标是最小化总损失函数,同时满足以下约束: $$
\begin{aligned}
& \min_{\mathbf{M}, \boldsymbol{\xi}} \quad (1 - \mu) \sum_{i,j \sim
i} (\bar{\boldsymbol{x}}_i - \bar{\boldsymbol{x}}_j)^\top \mathbf{M}
(\bar{\boldsymbol{x}}_i - \bar{\boldsymbol{x}}_j) + \mu \sum_{i,j \sim
i,l} (1 - y_{il}) \xi_{ijl} \\
& \text{s.t.} \quad (\bar{\boldsymbol{x}}_i -
\bar{\boldsymbol{x}}_l)^\top \mathbf{M} (\bar{\boldsymbol{x}}_i -
\bar{\boldsymbol{x}}_l) - (\bar{\boldsymbol{x}}_i -
\bar{\boldsymbol{x}}_j)^\top \mathbf{M} (\bar{\boldsymbol{x}}_i -
\bar{\boldsymbol{x}}_j) \geq 1 - \xi_{ijl}, \\
& \quad \quad \quad \xi_{ijl} \geq 0, \quad \mathbf{M} \succeq 0.
\end{aligned}
$$ -
约束(1):确保不同类样本对的距离比同类样本对大至少 $ 1
- {ijl} $。
- 约束(2):松弛变量 $ {ijl} $
允许部分样本对违反约束。
- 约束(3):$ $
必须是半正定矩阵,保证距离的非负性和三角不等式。
数据降维有哪些常用的方法?阐述主成分分析(PCA)算法的计算流程,并讨论PCA 降维之后的维度如何确定?
(1)常用数据降维方法
(2)主成分分析(PCA)的计算流程
(3)PCA降维后维度的确定
度量学习的目标是什么?LMNN算法中三元组损失是什么?如何计算?
(1)度量学习的目标
度量学习旨在学习一个合理的距离度量,使得: -
相似样本:距离尽可能小(如同类样本)。
- 不相似样本:距离尽可能大(如异类样本)。
典型应用包括推荐系统(优化用户-商品相似性)、图像检索(提升匹配精度)和生物识别(增强类间可分性)。
(2)LMNN中的三元组损失
LMNN(Large Margin Nearest Neighbor)是一种监督度量学习方法,其核心思想是通过优化距离度量来提升KNN的分类性能。虽然LMNN本身主要使用对比损失(Contrastive Loss),但三元组损失(Triplet Loss)是深度度量学习中常见的损失函数,其计算方式如下:三元组损失的定义
三元组损失基于锚点(Anchor)、正例(Positive)和负例(Negative)三个样本,目标是使锚点与正例的距离小于锚点与负例的距离,公式为:
ℒ = ∑i, j, lmax (0, ∥zi − zj∥2−∥zi − zl∥2 + m)
- $ _i $:锚点样本的嵌入表示。
- $ _j $:与锚点同类的正例样本。
- $ _l $:与锚点不同类的负例样本。
- $ m $:预设的边界值(Margin),控制正负样本距离的最小差距 。
LMNN的损失函数
LMNN 的损失函数包含两部分: 1. 拉力损失(Pull
Loss):最小化同类样本对的距离:
$$
\varepsilon_{\text{pull}} = \sum_{i,j \sim i}
\|\mathbf{L}(\bar{\boldsymbol{x}}_i - \bar{\boldsymbol{x}}_j)\|^2
$$ 2. 推力损失(Push
Loss):最大化异类样本对的距离:
$$
\varepsilon_{\text{push}} = \sum_{i,j \sim i,l} (1 - y_{il}) \left[1
+ \|\mathbf{L}(\bar{\boldsymbol{x}}_i - \bar{\boldsymbol{x}}_j)\|^2 -
\|\mathbf{L}(\bar{\boldsymbol{x}}_i -
\bar{\boldsymbol{x}}_l)\|^2\right]_+
$$ 其中 $ $ 是线性变换矩阵,$ y_{il} $ 表示样本对是否同类,$
[]_+ $ 表示取正值部分 。
优化目标
LMNN 的总损失为拉力和推力损失的加权和: ε(L) = (1 − μ)εpull + μεpush 参数 $ $ 平衡两类损失的权重,最终通过优化 $ $ 得到最优距离度量 。
监督学习解决现实问题有哪些难点? 1.标记数据获取成本高:在许多领域如医疗,获取标记数据是昂贵且耗时的。 2.未标记数据大量存在且易得:相对而言,未标记数据大量存在且容易获取。 3.提升模型的泛化能力:通过利用未标记数据,可以增强模型的泛化能力。 举例:在医疗领域,获取医生标记的诊断数据非常昂贵,但有大量未标记的病人记录。 半监督学习可以帮助利用这些未标记数据,提高疾病预测模型的准确性。
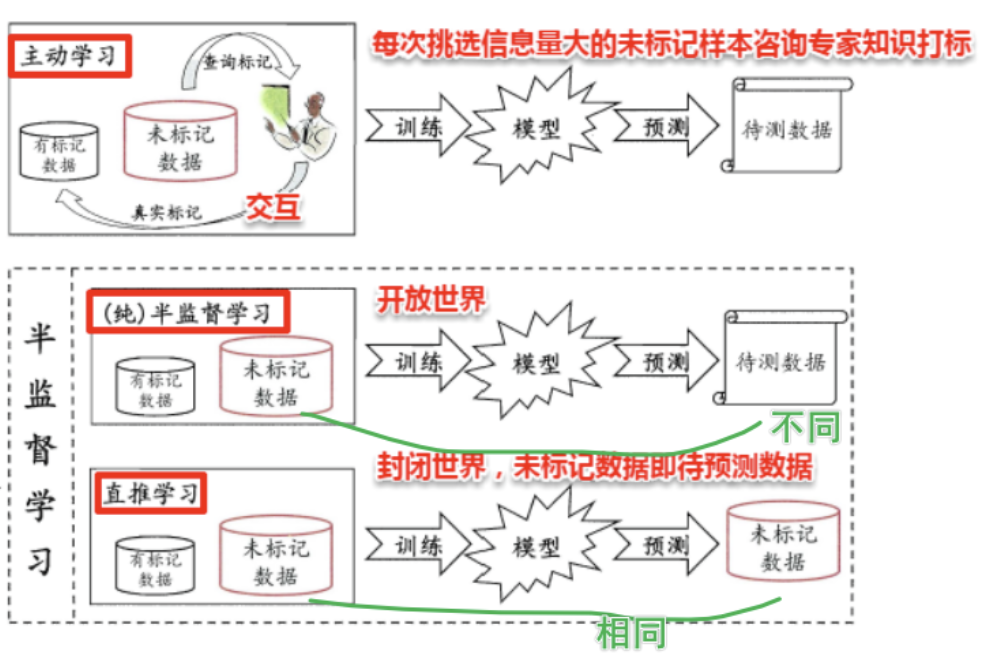 半监督学习结合了有监督学习和无监督学习,半监督学习使用少量的标记数据和大量的未标记数据来训练模型,主要目标是提升模型在未标记数据上的表现。
半监督学习结合了有监督学习和无监督学习,半监督学习使用少量的标记数据和大量的未标记数据来训练模型,主要目标是提升模型在未标记数据上的表现。
假设所有数据(无论是否有标记)都是由一个潜在的模型“生成”的。那么无标记的数据可以帮助更准确的估计潜在模型的参数。 比如右图中可以看到数据可以由两个高斯分布近似,则无监督的数据可以被用来更好得做高斯分布的参数估计

监督学习中的SVM试图找到一个划分超平面,使得两侧支持向量之间的间隔最大,即 最大划分间隔 思想。对于半监督SVM (Semi-Supervised Support Vector Machine, S3VM) 则考虑超平面在能将两类标记样本分隔的同时,穿过数据低密度的区域。
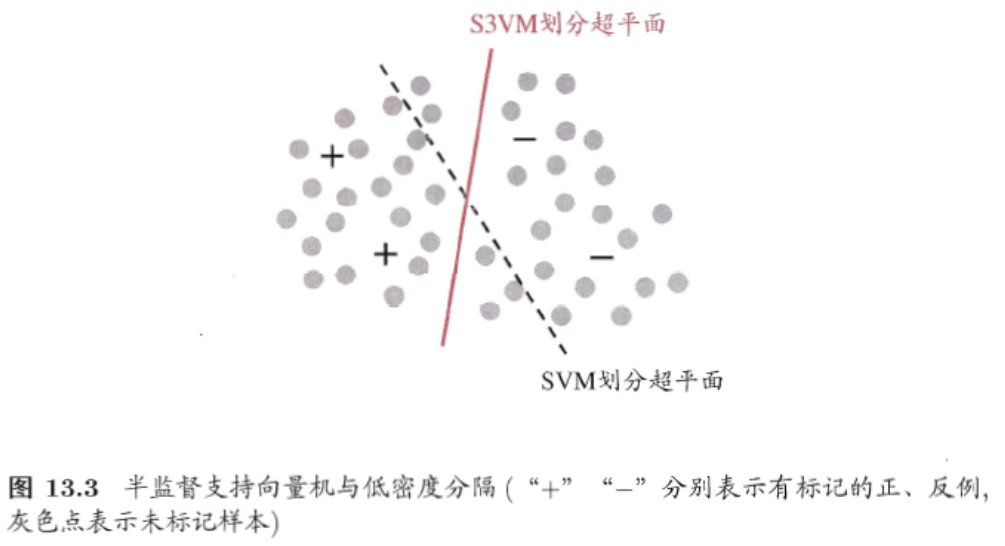
1. 核心思想
TSVM 是一种半监督学习方法,通过结合有标记数据 $ D_l
$ 和未标记数据 $ D_u
$,利用伪标签(Pseudo-labels)和迭代优化策略,最大化分类超平面的间隔。其损失函数需同时考虑:
- 有标记样本:最小化分类错误(Hinge Loss)。
- 未标记样本:通过伪标签引入约束,逐步调整超平面。
2. 损失函数推导
TSVM 的目标是找到一个超平面 $ ^ + b = 0 $,使得: 1.
有标记样本的分类误差最小。
2. 未标记样本的伪标签与超平面预测结果一致。
标准SVM的损失函数为: $$ \min_{\boldsymbol{w}, b, \xi} \quad \frac{1}{2} \|\boldsymbol{w}\|^2 + C \sum_{i=1}^l \xi_i $$ 其中,$ _i $ 是松弛变量,表示样本 $ (_i, y_i) $ 的分类误差。
TSVM的扩展:
引入未标记样本 $ D_u $ 的伪标签 $ j ( j = l+1, , l+u $),并赋予其较小的惩罚系数
$ C_u $(初始阶段 $ C_u C_l ):$
{, b, } ||^2 + C_l _{i=1}^l i + C_u {j=l+1}^{l+u} _j $$
其中: - $ C_l $:有标记样本的惩罚系数。
- $ C_u
$:未标记样本的惩罚系数,初始值很小,逐步增大以增强伪标签的影响。
3. 迭代优化流程
4. 关键数学细节
Hinge Loss:
对每个样本 $ (_i, y_i) ,损失为:$ _i =
(0, 1 - y_i (^_i + b)) $$ 未标记样本的伪标签 $ _j $
同样代入此公式,但惩罚系数为 $ C_u $。
正则化项:
$ ||^2 $ 确保超平面的泛化能力,防止过拟合。
伪标签翻转条件:
当两个未标记样本 $ i, j $ 满足: ŷiŷj < 0 且 ξi > 0, ξj > 0, ξi + ξj > 2
表示它们被错误分类且距离超平面较近,需翻转其中一个标签以减少冲突。
给定一个数据集,我们可将其映射为一个图,数据集中每个样本对应于图结点,若两个样本之间的相似度很高(或相关性很强),则对应的结点之间存在一条边,边的“强度”(strength) 正比于样本之间的相似度(或相关性)。
可将有标记样本所对应的结点想象为染过色,标记样本所对应的结点尚未染色。半监督学习就对应于“颜色”在图上扩散或传播的过程。由于个图对应了一个矩阵,我们就能基于矩阵运算来进行半监督学习算法的推导与分析。
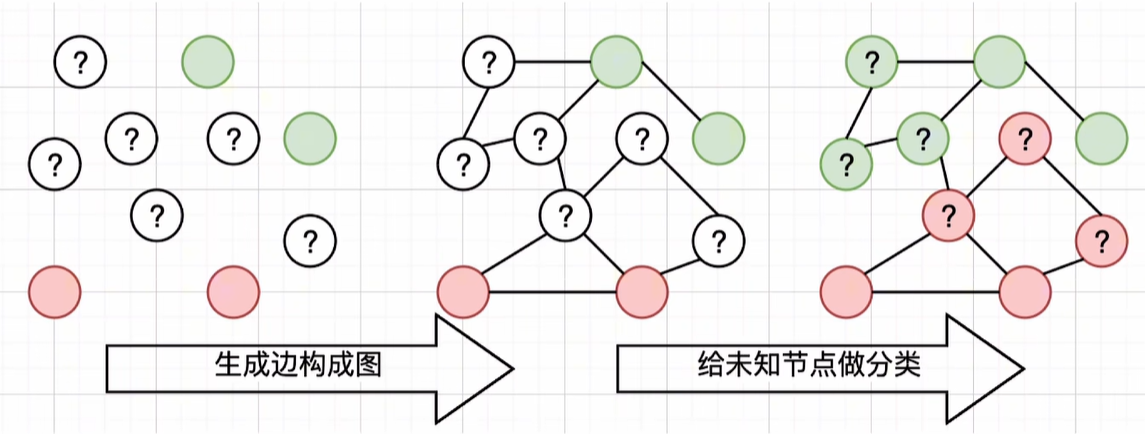
图半监督学习中的能量函数推导详解
1. 图结构与亲和矩阵
给定有标记数据集 $ D_l = {(1, y_1), (2, y_2), , (l, y_l)}
$ 和未标记数据集 $ D_u = {{l+1}, {l+2}, , {l+u}}
$,构建图 $ G = (V, E) : − * * 结点集 * *:
V = {1, , l, {l+1}, , {l+u}} $,包含所有样本。
- 边集:通过亲和矩阵 $ $ 表示,元素定义为: $$
(\mathbf{W})_{ij} =
\begin{cases}
\exp\left(-\frac{\|\boldsymbol{x}_i -
\boldsymbol{x}_j\|^2}{2\sigma^2}\right), & i \neq j \\
0, & \text{otherwise}
\end{cases}
$$ 其中,$ $ 是高斯核的带宽参数,控制邻接关系的敏感性。
2. 能量函数的定义与推导
假设分类模型的输出标记为 $ f(_i) $(取值为类别标签,如 $ $),定义能量函数 $ E(f) $ 为: $$ E(f) = \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m (\mathbf{W})_{ij} (f(\boldsymbol{x}_i) - f(\boldsymbol{x}_j))^2 $$ 其中 $ m = l + u $ 是总样本数。
3. 能量函数的展开与简化
图半监督学习方法推导详解
1. 分块矩阵表示
将亲和矩阵 $ $ 和度矩阵 $ $ 按有标记数据(前 $ l $
行列)和未标记数据(后 $ u $ 行列)分块: $$
\mathbf{W} =
\begin{bmatrix}
\mathbf{W}_{ll} & \mathbf{W}_{lu} \\
\mathbf{W}_{ul} & \mathbf{W}_{uu}
\end{bmatrix}, \quad
\mathbf{D} =
\begin{bmatrix}
\mathbf{D}_{ll} & \mathbf{0}_{lu} \\
\mathbf{0}_{ul} & \mathbf{D}_{uu}
\end{bmatrix}
$$ 其中: - $ {ll} $:有标记数据间的亲和度。
- $ {lu} $:有标记与未标记数据间的亲和度。
- $ {uu} $:未标记数据间的亲和度。
- $ {ll}, _{uu} $:对应子图的度矩阵。
2. 能量函数的分块展开
能量函数 $ E(f) = ^( - ) $ 可展开为
展开后得到: E(f) = fl⊤(Dll − Wll)fl − 2fu⊤Wulfl + fu⊤(Duu − Wuu)fu
**3. 对未标记数据 $ _u $ 求偏微分**
目标是最小化 $ E(f) $,对 $ _u $ 求偏导并令其为零: $$ \frac{\partial E(f)}{\partial \boldsymbol{f}_u} = -2 \mathbf{W}_{ul} \boldsymbol{f}_l + 2 (\mathbf{D}_{uu} - \mathbf{W}_{uu}) \boldsymbol{f}_u = 0 $$ 解得: fu = (Duu − Wuu)−1Wulfl
协同训练(Co-training)是一种经典的半监督学习方法,由Blum和Mitchell于1998年首次提出,主要用于处理多视图数据(Multi-view Data)。其核心思想是通过多个分类器的协作,利用少量标记数据和大量未标记数据提升模型性能。以下是详细解析:
1. 核心思想与假设
(1)多视图数据
(2)协作机制
2. 算法流程
3. 核心优势
什么是半监督学习?请简要描述其基本思想。半监督学习相比于监督学习和无监督学习有什么优势和应用场景?
(1)定义与基本思想
半监督学习(Semi-Supervised
Learning)是结合监督学习(利用标记数据)和无监督学习(利用未标记数据)的机器学习方法,其核心思想是通过少量标记数据与大量未标记数据的联合训练,提升模型的泛化能力和鲁棒性。
-
监督学习:依赖大量人工标注数据(如分类、回归)。
-
无监督学习:仅利用数据分布规律(如聚类、降维)。
-
半监督学习:在标记数据稀缺时,通过未标记数据挖掘潜在结构,降低标注成本
。
(2)优势
(3)应用场景
协同训练算法的作用是什么?请简述算法主要流程和所需条件。
(1)作用与核心思想
协同训练是一种典型的半监督学习方法,适用于多视图数据(Multi-view Data)。其核心思想是通过多个分类器的协作,利用未标记数据扩展训练集,最终提升模型性能。
(2)算法流程
(3)所需条件
智能天气提醒助手
描述:开发一款web应用,实时获取天气数据并支持个性化提醒(如雨天带伞)。
要求:
调用天气API获取实时数据(如OpenWeatherMap,每天1000次免费调用)
使用前端三件套设计交互界面,展示当前及未来天气信息,空气质量、体感温度、日出日落、月相等信息;
使用fastapi做后端
支持地点设置和天气提醒条件配置,在预设的提醒条件下提醒用户,并且将用户偏好保存至本地文件。
多城市切换、历史天气查询、全球地图展示等额外功能(可选*)。
fastapi,前端三件套(fetchapi),apifox
Fetch API
是现代浏览器提供的标准网络请求接口,允许开发者通过 JavaScript 发起异步
HTTP 请求(如 GET、POST、PUT、DELETE 等),并处理响应数据(如
JSON、文本、图片等)。它是传统
XMLHttpRequest(AJAX)的替代方案,语法更简洁,且支持
Promise 异步编程。
简单来说,就是用作给后端发送请求,实现前后端分离
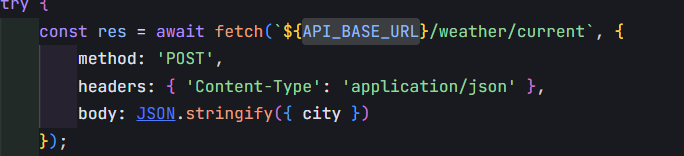
在使用 fetch 发起 HTTP
请求时,method、headers 和 body
是配置请求的核心参数,它们共同决定了请求的行为和数据格式。以下是每个参数的具体作用及示例:
method: 'POST'作用
指定 HTTP 请求的方法(动词),POST
表示向服务器提交数据(如创建资源)。 - 常见方法: -
GET:获取数据(默认方法,无需显式声明)。 -
POST:提交数据(如新增记录)。 -
PUT:更新数据。 - DELETE:删除数据。 -
与后端交互:FastAPI 的路由通过
@app.post()、@app.get()
等装饰器匹配请求方法。
示例
1 | fetch('https://api.example.com/submit', { |
headers
请求头作用
定义请求的元信息,用于告知服务器如何处理请求和数据格式。 -
关键字段: -
Content-Type:指定请求体(body)的数据格式。
- application/json:表示发送 JSON 数据。 -
application/x-www-form-urlencoded:表示表单数据(键值对)。
- multipart/form-data:用于上传文件。 -
Authorization:携带身份凭证(如 Token)。
- Accept:声明客户端期望的响应格式(如
JSON、XML)。
示例
1 | headers: { |
body: JSON.stringify(item)作用
定义请求体(即发送给服务器的数据),需根据 Content-Type
的类型进行格式化。 -
JSON.stringify(item):将 JavaScript
对象转换为 JSON 字符串。 - 因为 HTTP
协议只能传输文本,不能直接传输对象。 - 注意事项: -
若未设置
Content-Type: application/json,服务器可能无法正确解析数据。
- 若使用 FormData 上传文件,需使用
multipart/form-data 格式。
示例
1 | const item = { name: "Apple", price: 1.99 }; |
FastAPI 后端定义
1 | from fastapi import FastAPI |
前端调用
1 | const item = { name: "Banana", price: 0.99 }; |
| 参数 | 作用 | 必填性 |
|---|---|---|
method |
定义请求类型(如 POST) |
必填(非 GET 时) |
headers |
声明数据格式、身份凭证等 | 必填(尤其 Content-Type) |
body |
发送的数据(需格式化为字符串) | 必填(POST/PUT 时) |
关键点:
- POST 请求必须设置 headers['Content-Type'] 和
body。 - JSON.stringify() 是发送 JSON
数据的关键步骤。 - FastAPI 会根据 Content-Type
自动解析请求体并进行数据校验(通过 Pydantic 模型)。
CORS(Cross-Origin Resource Sharing) 是一种浏览器安全机制,用于解决 跨域请求 的问题。它允许服务器明确授权某些跨域请求,从而在保障安全的前提下,实现前后端分离架构中的跨域通信。
1. 同源策略(Same-Origin Policy)
浏览器默认遵循 同源策略,即网页只能请求与自身
同源(相同域名、协议、端口) 的资源。
例如:
http://localhost:3000http://localhost:80002. 跨域场景
跨域是前后端分离架构中的常见问题,例如: - 前端部署在
https://example.com,后端 API 在
https://api.example.com。 -
前端本地开发(localhost:3000)调用后端服务(localhost:8000)。
3. CORS 的作用
CORS 通过 服务器响应头
告诉浏览器:“这个跨域请求是安全的,允许它通过”。
浏览器根据这些响应头决定是否放行请求。
以 FastAPI 为例,配置允许跨域请求的步骤如下:
启用 CORS 中间件
1 | from fastapi import FastAPI |
1. 前后端分离开发
localhost:3000,后端(FastAPI)运行在
localhost:8000。allow_origins=["http://localhost:3000"]
允许跨域通信。2. 第三方 API 调用
Access-Control-Allow-Origin: *
表示允许所有来源。3. 需要凭证的场景
1 | app.add_middleware( |
| 概念 | 作用 | 配置示例 |
|---|---|---|
| 同源策略 | 浏览器安全机制,阻止跨域请求 | 默认启用 |
| CORS | 服务器通过响应头授权跨域请求 | Access-Control-Allow-Origin |
| 预检请求 | OPTIONS 请求,验证复杂跨域请求的合法性 | 自动触发 |
| FastAPI 配置 | 使用 CORSMiddleware 中间件 |
app.add_middleware(...) |
最佳实践: 1.
开发阶段:允许所有来源(allow_origins=["*"]),方便调试。
2.
生产环境:严格限制允许的源、方法、头信息,避免安全风险。
3. 携带凭证:启用 allow_credentials=True
并明确指定允许的源(避免使用 *)。
Nginx(发音为 “engine-x”)是一个高性能的开源 Web 服务器、反向代理服务器、负载均衡器和 HTTP 缓存,广泛用于现代 Web 架构中。它以轻量级、低资源消耗和高并发处理能力著称,常用于优化网站性能、管理流量和提升安全性。
1. Web 服务器
2. 反向代理
3. 负载均衡
4. SSL/TLS 终端
5. 缓存
6. 高可用性和容错
1. 反向代理 FastAPI 服务
1 | # /etc/nginx/sites-available/fastapi.conf |
example.com
的请求转发给运行在 127.0.0.1:8000 的 FastAPI 服务。2. 静态文件托管
1 | location /static/ { |
/var/www/static/
目录下的静态文件(如图片、CSS)。1 | 客户端 -> Nginx(反向代理) -> FastAPI(处理业务逻辑) -> 数据库/其他服务 |
最佳实践:
uvicorn main:app --reload)。通过 Nginx 的反向代理和负载均衡,可以显著提升 FastAPI 应用的性能、安全性和可扩展性。
反向代理(Reverse Proxy) 是一种服务器角色,它位于客户端与服务器之间,接收客户端的请求后,将请求转发给后端服务器(如 FastAPI、Django、Node.js 等),并将后端服务器的响应返回给客户端。它的核心作用是隐藏后端服务器的真实地址,优化请求处理流程,并增强安全性。
反向代理是现代 Web 架构中不可或缺的组件,尤其在前后端分离、微服务、高并发场景下作用显著。通过 Nginx 等工具实现反向代理,可以: - 提升安全性(隐藏后端、过滤攻击)。 - 优化性能(负载均衡、缓存静态资源)。 - 简化运维(集中管理 SSL、日志)。
对于 FastAPI 项目,推荐在生产环境中使用 Nginx 作为反向代理,以充分发挥其高性能和灵活性优势。
二级域名(Second-Level Domain, SLD) 是域名系统(DNS)中的一个层级,通常位于顶级域名(TLD)之下,主域名(一级域名)之上。它是域名结构中的关键部分,用于标识网站或服务的主体。
域名层级结构
域名由多个层级组成,从右向左层级递增,具体如下:
1 | mail.example.com |
1. 顶级域名(TLD)
.com(商业)、.org(非营利组织)、.net(网络服务)、.cn(中国)、.jp(日本)。2. 二级域名(SLD)
example.com
中,example 是二级域名。3. 子域名(Subdomain)
mail.example.com
中,mail 是子域名。二级域名的常见用途
google.com、apple.com。mail.google.com:邮件服务drive.google.com:云存储服务maps.google.com:地图服务fr.wikipedia.org(法语版)zh.wikipedia.org(中文版)DOM(Document Object Model,文档对象模型)
是浏览器将 HTML 或 XML 文档解析为树状结构的编程接口。DOM
元素 是构成这棵树的节点(如
<div>、<p>、<button>
等),它们不仅是页面内容的载体,更是实现动态交互的核心工具。
获取apihttps://home.openweathermap.org/api_keys
api文档Weather API - OpenWeatherMap
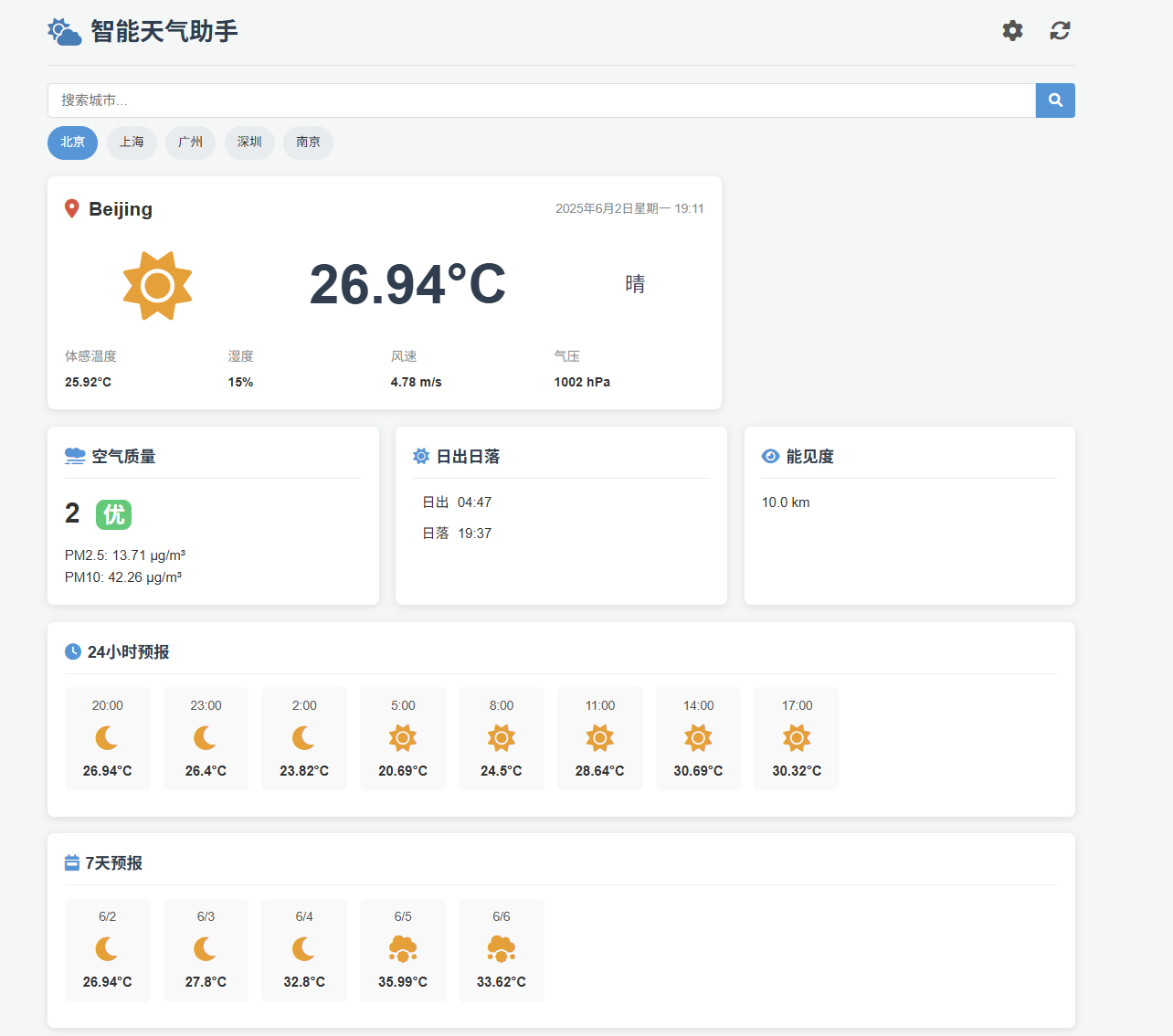
完成基本天气功能的开发
完成ai建议功能
复习:在前面我们已经学习了Pandas基础,知道利用Pandas读取csv数据的增删查改,今天我们要学习的就是探索性数据分析,主要介绍如何利用Pandas进行排序、算术计算以及计算描述函数describe()的使用。
1 | #加载所需的库 |
1 | #载入之前保存的train_chinese.csv数据,关于泰坦尼克号的任务,我们就使用这个数据 |
教材《Python for Data Analysis》第五章
1 | # 具体请看《利用Python进行数据分析》第五章 排序和排名 部分 |
| d | a | b | c | |
|---|---|---|---|---|
| 2 | 0 | 1 | 2 | 3 |
| 1 | 4 | 5 | 6 | 7 |
【代码解析】
pd.DataFrame() :创建一个DataFrame对象
np.arange(8).reshape((2, 4)) : 生成一个二维数组(2*4),第一列:0,1,2,3 第二列:4,5,6,7
index=[’2, 1] :DataFrame 对象的索引列
columns=[‘d’, ‘a’, ‘b’, ‘c’] :DataFrame 对象的索引行
【问题】:大多数时候我们都是想根据列的值来排序,所以将你构建的DataFrame中的数据根据某一列,升序排列
1 | #回答代码 |
| d | a | b | c | |
|---|---|---|---|---|
| 1 | 4 | 5 | 6 | 7 |
| 2 | 0 | 1 | 2 | 3 |
【思考】通过书本你能说出Pandas对DataFrame数据的其他排序方式吗?
【总结】下面将不同的排序方式做一个总结
1.让行索引升序排序
1 | #代码 |
| d | a | b | c | |
|---|---|---|---|---|
| 1 | 4 | 5 | 6 | 7 |
| 2 | 0 | 1 | 2 | 3 |
2.让列索引升序排序
1 | #代码 |
| a | b | c | d | |
|---|---|---|---|---|
| 2 | 1 | 2 | 3 | 0 |
| 1 | 5 | 6 | 7 | 4 |
3.让列索引降序排序
1 | #代码 |
| d | c | b | a | |
|---|---|---|---|---|
| 2 | 0 | 3 | 2 | 1 |
| 1 | 4 | 7 | 6 | 5 |
4.让任选两列数据同时降序排序
1 | #代码 |
| d | a | b | c | |
|---|---|---|---|---|
| 1 | 4 | 5 | 6 | 7 |
| 2 | 0 | 1 | 2 | 3 |
1 | ''' |
| 乘客ID | 是否幸存 | 仓位等级 | 姓名 | 性别 | 年龄 | 兄弟姐妹个数 | 父母子女个数 | 船票信息 | 票价 | 客舱 | 登船港口 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 679 | 680 | 1 | 1 | Cardeza, Mr. Thomas Drake Martinez | male | 36.0 | 0 | 1 | PC 17755 | 512.3292 | B51 B53 B55 | C |
| 258 | 259 | 1 | 1 | Ward, Miss. Anna | female | 35.0 | 0 | 0 | PC 17755 | 512.3292 | NaN | C |
| 737 | 738 | 1 | 1 | Lesurer, Mr. Gustave J | male | 35.0 | 0 | 0 | PC 17755 | 512.3292 | B101 | C |
| 438 | 439 | 0 | 1 | Fortune, Mr. Mark | male | 64.0 | 1 | 4 | 19950 | 263.0000 | C23 C25 C27 | S |
| 341 | 342 | 1 | 1 | Fortune, Miss. Alice Elizabeth | female | 24.0 | 3 | 2 | 19950 | 263.0000 | C23 C25 C27 | S |
| 88 | 89 | 1 | 1 | Fortune, Miss. Mabel Helen | female | 23.0 | 3 | 2 | 19950 | 263.0000 | C23 C25 C27 | S |
| 27 | 28 | 0 | 1 | Fortune, Mr. Charles Alexander | male | 19.0 | 3 | 2 | 19950 | 263.0000 | C23 C25 C27 | S |
| 742 | 743 | 1 | 1 | Ryerson, Miss. Susan Parker “Suzette” | female | 21.0 | 2 | 2 | PC 17608 | 262.3750 | B57 B59 B63 B66 | C |
| 311 | 312 | 1 | 1 | Ryerson, Miss. Emily Borie | female | 18.0 | 2 | 2 | PC 17608 | 262.3750 | B57 B59 B63 B66 | C |
| 299 | 300 | 1 | 1 | Baxter, Mrs. James (Helene DeLaudeniere Chaput) | female | 50.0 | 0 | 1 | PC 17558 | 247.5208 | B58 B60 | C |
| 118 | 119 | 0 | 1 | Baxter, Mr. Quigg Edmond | male | 24.0 | 0 | 1 | PC 17558 | 247.5208 | B58 B60 | C |
| 380 | 381 | 1 | 1 | Bidois, Miss. Rosalie | female | 42.0 | 0 | 0 | PC 17757 | 227.5250 | NaN | C |
| 716 | 717 | 1 | 1 | Endres, Miss. Caroline Louise | female | 38.0 | 0 | 0 | PC 17757 | 227.5250 | C45 | C |
| 700 | 701 | 1 | 1 | Astor, Mrs. John Jacob (Madeleine Talmadge Force) | female | 18.0 | 1 | 0 | PC 17757 | 227.5250 | C62 C64 | C |
| 557 | 558 | 0 | 1 | Robbins, Mr. Victor | male | NaN | 0 | 0 | PC 17757 | 227.5250 | NaN | C |
| 527 | 528 | 0 | 1 | Farthing, Mr. John | male | NaN | 0 | 0 | PC 17483 | 221.7792 | C95 | S |
| 377 | 378 | 0 | 1 | Widener, Mr. Harry Elkins | male | 27.0 | 0 | 2 | 113503 | 211.5000 | C82 | C |
| 779 | 780 | 1 | 1 | Robert, Mrs. Edward Scott (Elisabeth Walton Mc… | female | 43.0 | 0 | 1 | 24160 | 211.3375 | B3 | S |
| 730 | 731 | 1 | 1 | Allen, Miss. Elisabeth Walton | female | 29.0 | 0 | 0 | 24160 | 211.3375 | B5 | S |
| 689 | 690 | 1 | 1 | Madill, Miss. Georgette Alexandra | female | 15.0 | 0 | 1 | 24160 | 211.3375 | B5 | S |
1 | #代码 |
【思考】排序后,如果我们仅仅关注年龄和票价两列。根据常识我知道发现票价越高的应该客舱越好,所以我们会明显看出,票价前20的乘客中存活的有14人,这是相当高的一个比例,那么我们后面是不是可以进一步分析一下票价和存活之间的关系,年龄和存活之间的关系呢?当你开始发现数据之间的关系了,数据分析就开始了。
当然,这只是我的想法,你还可以有更多想法,欢迎写在你的学习笔记中。
多做几个数据的排序
1 | # 具体请看《利用Python进行数据分析》第五章 算术运算与数据对齐 部分 |
( a b c
one 0.0 1.0 2.0
two 3.0 4.0 5.0
three 6.0 7.0 8.0,
a e c
first 0.0 1.0 2.0
one 3.0 4.0 5.0
two 6.0 7.0 8.0
second 9.0 10.0 11.0)将frame_a和frame_b进行相加
1 | #代码 |
| a | b | c | e | |
|---|---|---|---|---|
| first | NaN | NaN | NaN | NaN |
| one | 3.0 | NaN | 7.0 | NaN |
| second | NaN | NaN | NaN | NaN |
| three | NaN | NaN | NaN | NaN |
| two | 9.0 | NaN | 13.0 | NaN |
【提醒】两个DataFrame相加后,会返回一个新的DataFrame,对应的行和列的值会相加,没有对应的会变成空值NaN。
当然,DataFrame还有很多算术运算,如减法,除法等,有兴趣的同学可以看《利用Python进行数据分析》第五章
算术运算与数据对齐 部分,多在网络上查找相关学习资料。
1 | ''' |
10【提醒】我们只需找出”兄弟姐妹个数“和”父母子女个数“之和最大的数,当然你还可以想出很多方法和思考角度,欢迎你来说出你的看法。
多做几个数据的相加,看看你能分析出什么?
1 | #(1) 关键知识点示例做一遍(简单数据) |
| one | two | |
|---|---|---|
| a | 1.40 | NaN |
| b | 7.10 | -4.5 |
| c | NaN | NaN |
| d | 0.75 | -1.3 |
1 | #代码 |
| one | two | |
|---|---|---|
| count | 3.000000 | 2.000000 |
| mean | 3.083333 | -2.900000 |
| std | 3.493685 | 2.262742 |
| min | 0.750000 | -4.500000 |
| 25% | 1.075000 | -3.700000 |
| 50% | 1.400000 | -2.900000 |
| 75% | 4.250000 | -2.100000 |
| max | 7.100000 | -1.300000 |
调用 describe 函数,观察frame2的数据基本信息
1 | ''' |
'\n看看泰坦尼克号数据集中 票价 这列数据的基本统计数据\n'1 | #代码 |
count 891.000000
mean 32.204208
std 49.693429
min 0.000000
25% 7.910400
50% 14.454200
75% 31.000000
max 512.329200
Name: 票价, dtype: float64【思考】从上面数据我们可以看出, 一共有891个票价数据, 平均值约为:32.20, 标准差约为49.69,说明票价波动特别大, 25%的人的票价是低于7.91的,50%的人的票价低于14.45,75%的人的票价低于31.00, 票价最大值约为512.33,最小值为0。 当然,答案只是我的想法,你还可以有更多想法,欢迎写在你的学习笔记中。
多做几个组数据的统计,看看你能分析出什么?
1 | # 写下你的其他分析 |
count 891.000000
mean 0.381594
std 0.806057
min 0.000000
25% 0.000000
50% 0.000000
75% 0.000000
max 6.000000
Name: 父母子女个数, dtype: float64【思考】有更多想法,欢迎写在你的学习笔记中。
【总结】本节中我们通过Pandas的一些内置函数对数据进行了初步统计查看,这个过程最重要的不是大家得掌握这些函数,而是看懂从这些函数出来的数据,构建自己的数据分析思维,这也是第一章最重要的点,希望大家学完第一章能对数据有个基本认识,了解自己在做什么,为什么这么做,后面的章节我们将开始对数据进行清洗,进一步分析。
复习:这门课程得主要目的是通过真实的数据,以实战的方式了解数据分析的流程和熟悉数据分析python的基本操作。知道了课程的目的之后,我们接下来我们要正式的开始数据分析的实战教学,完成kaggle上泰坦尼克的任务,实战数据分析全流程。 这里有两份资料: 教材《Python for Data Analysis》和 baidu.com & google.com(善用搜索引擎)
数据集下载 https://www.kaggle.com/c/titanic/overview
1 | #写入代码 |
【提示】如果加载失败,学会如何在你的python环境下安装numpy和pandas这两个库
1 | #写入代码 |
1 | #写入代码 |
/workspace/WuTeachingAI/hands-on-data-analysis/myself/titanic/test.csv
/workspace/WuTeachingAI/hands-on-data-analysis/myself/titanic/train.csv| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th… | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
【提示】相对路径载入报错时,尝试使用os.getcwd()查看当前工作目录。
【思考】知道数据加载的方法后,试试pd.read_csv()和pd.read_table()的不同,如果想让他们效果一样,需要怎么做?了解一下’.tsv’和’.csv’的不同,如何加载这两个数据集?
【总结】加载的数据是所有工作的第一步,我们的工作会接触到不同的数据格式(eg:.csv;.tsv;.xlsx),但是加载的方法和思路都是一样的,在以后工作和做项目的过程中,遇到之前没有碰到的问题,要多多查资料吗,使用googel,了解业务逻辑,明白输入和输出是什么。
1 | # pd.read_csv() 和 pd.read_table() 本质上非常相似,主要区别在于默认的分隔符参数。 |
1 | #写入代码 |
PassengerId Survived Pclass \
0 1 0 3
1 2 1 1
2 3 1 3
3 4 1 1
4 5 0 3
.. ... ... ...
886 887 0 2
887 888 1 1
888 889 0 3
889 890 1 1
890 891 0 3
Name Sex Age SibSp \
0 Braund, Mr. Owen Harris male 22.0 1
1 Cumings, Mrs. John Bradley (Florence Briggs Th... female 38.0 1
2 Heikkinen, Miss. Laina female 26.0 0
3 Futrelle, Mrs. Jacques Heath (Lily May Peel) female 35.0 1
4 Allen, Mr. William Henry male 35.0 0
.. ... ... ... ...
886 Montvila, Rev. Juozas male 27.0 0
887 Graham, Miss. Margaret Edith female 19.0 0
888 Johnston, Miss. Catherine Helen "Carrie" female NaN 1
889 Behr, Mr. Karl Howell male 26.0 0
890 Dooley, Mr. Patrick male 32.0 0
Parch Ticket Fare Cabin Embarked
0 0 A/5 21171 7.2500 NaN S
1 0 PC 17599 71.2833 C85 C
2 0 STON/O2. 3101282 7.9250 NaN S
3 0 113803 53.1000 C123 S
4 0 373450 8.0500 NaN S
.. ... ... ... ... ...
886 0 211536 13.0000 NaN S
887 0 112053 30.0000 B42 S
888 2 W./C. 6607 23.4500 NaN S
889 0 111369 30.0000 C148 C
890 0 370376 7.7500 NaN Q
[891 rows x 12 columns]【思考】什么是逐块读取?为什么要逐块读取呢?
【提示】大家可以chunker(数据块)是什么类型?用for循环打印出来出处具体的样子是什么?
1 | # **什么是逐块读取?** |
PassengerId => 乘客ID
Survived => 是否幸存
Pclass => 乘客等级(1/2/3等舱位)
Name => 乘客姓名
Sex => 性别
Age => 年龄
SibSp => 堂兄弟/妹个数
Parch => 父母与小孩个数
Ticket => 船票信息
Fare => 票价
Cabin => 客舱
Embarked => 登船港口
1 | #写入代码 |
| 是否幸存 | 仓位等级 | 姓名 | 性别 | 年龄 | 兄弟姐妹个数 | 父母子女个数 | 船票信息 | 票价 | 客舱 | 登船港口 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 乘客ID | |||||||||||
| 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th… | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
【思考】所谓将表头改为中文其中一个思路是:将英文列名表头替换成中文。还有其他的方法吗?
导入数据后,你可能要对数据的整体结构和样例进行概览,比如说,数据大小、有多少列,各列都是什么格式的,是否包含null等
1 | #写入代码 |
<class 'pandas.core.frame.DataFrame'>
Index: 891 entries, 1 to 891
Data columns (total 11 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 是否幸存 891 non-null int64
1 仓位等级 891 non-null int64
2 姓名 891 non-null object
3 性别 891 non-null object
4 年龄 714 non-null float64
5 兄弟姐妹个数 891 non-null int64
6 父母子女个数 891 non-null int64
7 船票信息 891 non-null object
8 票价 891 non-null float64
9 客舱 204 non-null object
10 登船港口 889 non-null object
dtypes: float64(2), int64(4), object(5)
memory usage: 83.5+ KB| 是否幸存 | 仓位等级 | 年龄 | 兄弟姐妹个数 | 父母子女个数 | 票价 | |
|---|---|---|---|---|---|---|
| count | 891.000000 | 891.000000 | 714.000000 | 891.000000 | 891.000000 | 891.000000 |
| mean | 0.383838 | 2.308642 | 29.699118 | 0.523008 | 0.381594 | 32.204208 |
| std | 0.486592 | 0.836071 | 14.526497 | 1.102743 | 0.806057 | 49.693429 |
| min | 0.000000 | 1.000000 | 0.420000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 0.000000 | 2.000000 | 20.125000 | 0.000000 | 0.000000 | 7.910400 |
| 50% | 0.000000 | 3.000000 | 28.000000 | 0.000000 | 0.000000 | 14.454200 |
| 75% | 1.000000 | 3.000000 | 38.000000 | 1.000000 | 0.000000 | 31.000000 |
| max | 1.000000 | 3.000000 | 80.000000 | 8.000000 | 6.000000 | 512.329200 |
【提示】有多个函数可以这样做,你可以做一下总结
1 | #写入代码 |
| 是否幸存 | 仓位等级 | 姓名 | 性别 | 年龄 | 兄弟姐妹个数 | 父母子女个数 | 船票信息 | 票价 | 客舱 | 登船港口 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 乘客ID | |||||||||||
| 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th… | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
| 6 | 0 | 3 | Moran, Mr. James | male | NaN | 0 | 0 | 330877 | 8.4583 | NaN | Q |
| 7 | 0 | 1 | McCarthy, Mr. Timothy J | male | 54.0 | 0 | 0 | 17463 | 51.8625 | E46 | S |
| 8 | 0 | 3 | Palsson, Master. Gosta Leonard | male | 2.0 | 3 | 1 | 349909 | 21.0750 | NaN | S |
| 9 | 1 | 3 | Johnson, Mrs. Oscar W (Elisabeth Vilhelmina Berg) | female | 27.0 | 0 | 2 | 347742 | 11.1333 | NaN | S |
| 10 | 1 | 2 | Nasser, Mrs. Nicholas (Adele Achem) | female | 14.0 | 1 | 0 | 237736 | 30.0708 | NaN | C |
| 11 | 1 | 3 | Sandstrom, Miss. Marguerite Rut | female | 4.0 | 1 | 1 | PP 9549 | 16.7000 | G6 | S |
| 12 | 1 | 1 | Bonnell, Miss. Elizabeth | female | 58.0 | 0 | 0 | 113783 | 26.5500 | C103 | S |
| 13 | 0 | 3 | Saundercock, Mr. William Henry | male | 20.0 | 0 | 0 | A/5. 2151 | 8.0500 | NaN | S |
| 14 | 0 | 3 | Andersson, Mr. Anders Johan | male | 39.0 | 1 | 5 | 347082 | 31.2750 | NaN | S |
| 15 | 0 | 3 | Vestrom, Miss. Hulda Amanda Adolfina | female | 14.0 | 0 | 0 | 350406 | 7.8542 | NaN | S |
1 | #写入代码 |
1 | #写入代码 |
| 是否幸存 | 仓位等级 | 姓名 | 性别 | 年龄 | 兄弟姐妹个数 | 父母子女个数 | 船票信息 | 票价 | 客舱 | 登船港口 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 乘客ID | |||||||||||
| 1 | False | False | False | False | False | False | False | False | False | True | False |
| 2 | False | False | False | False | False | False | False | False | False | False | False |
| 3 | False | False | False | False | False | False | False | False | False | True | False |
| 4 | False | False | False | False | False | False | False | False | False | False | False |
| 5 | False | False | False | False | False | False | False | False | False | True | False |
【总结】上面的操作都是数据分析中对于数据本身的观察
【思考】对于一个数据,还可以从哪些方面来观察?找找答案,这个将对下面的数据分析有很大的帮助
1 | #写入代码 |
【总结】数据的加载以及入门,接下来就要接触数据本身的运算,我们将主要掌握numpy和pandas在工作和项目场景的运用。
复习:在前面我们已经学习了Pandas基础,第二章我们开始进入数据分析的业务部分,在第二章第一节的内容中,我们学习了数据的清洗,这一部分十分重要,只有数据变得相对干净,我们之后对数据的分析才可以更有力。而这一节,我们要做的是数据重构,数据重构依旧属于数据理解(准备)的范围。
1 | # 导入基本库 |
1 | # 载入上一个任务人保存的文件中:result.csv,并查看这个文件 |
| Unnamed: 0 | PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th… | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
1 | #写入心得 |
1 | # 写入代码 |
{'female': [1, 2, 3, 8, 9, 10, 11, 14, 15, 18, 19, 22, 24, 25, 28, 31, 32, 38, 39, 40, 41, 43, 44, 47, 49, 52, 53, 56, 58, 61, 66, 68, 71, 79, 82, 84, 85, 88, 98, 100, 106, 109, 111, 113, 114, 119, 123, 128, 132, 133, 136, 140, 141, 142, 147, 151, 156, 161, 166, 167, 172, 177, 180, 184, 186, 190, 192, 194, 195, 198, 199, 205, 208, 211, 215, 216, 218, 229, 230, 233, 235, 237, 240, 241, 246, 247, 251, 254, 255, 256, 257, 258, 259, 264, 268, 269, 272, 274, 275, 276, ...], 'male': [0, 4, 5, 6, 7, 12, 13, 16, 17, 20, 21, 23, 26, 27, 29, 30, 33, 34, 35, 36, 37, 42, 45, 46, 48, 50, 51, 54, 55, 57, 59, 60, 62, 63, 64, 65, 67, 69, 70, 72, 73, 74, 75, 76, 77, 78, 80, 81, 83, 86, 87, 89, 90, 91, 92, 93, 94, 95, 96, 97, 99, 101, 102, 103, 104, 105, 107, 108, 110, 112, 115, 116, 117, 118, 120, 121, 122, 124, 125, 126, 127, 129, 130, 131, 134, 135, 137, 138, 139, 143, 144, 145, 146, 148, 149, 150, 152, 153, 154, 155, ...]}
Sex
female 44.479818
male 25.523893
Name: Fare, dtype: float64在了解GroupBy机制之后,运用这个机制完成一系列的操作,来达到我们的目的。
下面通过几个任务来熟悉GroupBy机制。
1 | # 写入代码 |
Sex
female 233
male 109
Name: Survived, dtype: int641 | # 写入代码 |
Pclass
1 136
2 87
3 119
Name: Survived, dtype: int64【提示:】表中的存活那一栏,可以发现如果还活着记为1,死亡记为0
【思考】从数据分析的角度,上面的统计结果可以得出那些结论
【思考】从任务二到任务三中,这些运算可以通过agg()函数来同时计算。并且可以使用rename函数修改列名。你可以按照提示写出这个过程吗?
1 | #思考心得 |
| mean_fare | count_pclass | |
|---|---|---|
| Sex | ||
| female | 44.479818 | 314 |
| male | 25.523893 | 577 |
1 | # 写入代码 |
Pclass Age
1 0.92 151.5500
2.00 151.5500
4.00 81.8583
11.00 120.0000
14.00 120.0000
Name: Fare, dtype: float641 | # 写入代码 |
1 | # 写入代码 |
Age
0.42 1
0.67 1
0.75 2
0.83 2
0.92 1
Name: Survived, dtype: int641 | # 写入代码 |
Age
24.0 15
Name: Survived, dtype: int641 | _sum = text['Survived'].sum() |
3421 | print("sum of person:"+str(_sum)) |
sum of person:342
最大存活率:0.043859649122807015经过前面的两章的知识点的学习,我可以对数数据的本身进行处理,比如数据本身的增删查补,还可以做必要的清洗工作。那么下面我们就要开始使用我们前面处理好的数据了。这一章我们要做的就是使用数据,我们做数据分析的目的也就是,运用我们的数据以及结合我的业务来得到某些我们需要知道的结果。那么分析的第一步就是建模,搭建一个预测模型或者其他模型;我们从这个模型的到结果之后,我们要分析我的模型是不是足够的可靠,那我就需要评估这个模型。今天我们学习建模,下一节我们学习评估。
我们拥有的泰坦尼克号的数据集,那么我们这次的目的就是,完成泰坦尼克号存活预测这个任务。
1 | import pandas as pd |
1 | %matplotlib inline |
1 | plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签 |
载入这些库,如果缺少某些库,请安装他们
【思考】这些库的作用是什么呢?你需要查一查
1 | #思考题回答 |
'\nImage 是 IPython.display 模块的一部分,用于在 Jupyter Notebook 或 IPython 环境中直接显示图像。支持从本地路径或网络 URL 加载图像,并控制显示格式(如宽度、高度、格式类型)\nseaborn 是一个基于 Matplotlib 的高级数据可视化库,专注于统计图形的绘制(如分布图、相关性图、分类图等),能快速生成美观且信息丰富的图表\n'1 | %matplotlib inline |
载入我们提供清洗之后的数据(clear_data.csv),大家也将原始数据载入(train.csv),说说他们有什么不同
1 | #写入代码 |
(891, 12)1 | #写入代码 |
.dataframe tbody tr th {
vertical-align: top;
}
.dataframe thead th {
text-align: right;
}| PassengerId | Survived | Pclass | Name | Sex | Age | SibSp | Parch | Ticket | Fare | Cabin | Embarked | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 3 | Braund, Mr. Owen Harris | male | 22.0 | 1 | 0 | A/5 21171 | 7.2500 | NaN | S |
| 1 | 2 | 1 | 1 | Cumings, Mrs. John Bradley (Florence Briggs Th… | female | 38.0 | 1 | 0 | PC 17599 | 71.2833 | C85 | C |
| 2 | 3 | 1 | 3 | Heikkinen, Miss. Laina | female | 26.0 | 0 | 0 | STON/O2. 3101282 | 7.9250 | NaN | S |
| 3 | 4 | 1 | 1 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | female | 35.0 | 1 | 0 | 113803 | 53.1000 | C123 | S |
| 4 | 5 | 0 | 3 | Allen, Mr. William Henry | male | 35.0 | 0 | 0 | 373450 | 8.0500 | NaN | S |
1 | #写入代码 |
| PassengerId | Pclass | Age | SibSp | Parch | Fare | Sex_female | Sex_male | Embarked_C | Embarked_Q | Embarked_S | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 3 | 22.0 | 1 | 0 | 7.2500 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 38.0 | 1 | 0 | 71.2833 | 1 | 0 | 1 | 0 | 0 |
| 2 | 2 | 3 | 26.0 | 0 | 0 | 7.9250 | 1 | 0 | 0 | 0 | 1 |
| 3 | 3 | 1 | 35.0 | 1 | 0 | 53.1000 | 1 | 0 | 0 | 0 | 1 |
| 4 | 4 | 3 | 35.0 | 0 | 0 | 8.0500 | 0 | 1 | 0 | 0 | 1 |
这里我的建模,并不是从零开始,自己一个人完成完成所有代码的编译。我们这里使用一个机器学习最常用的一个库(sklearn)来完成我们的模型的搭建
下面给出sklearn的算法选择路径,供大家参考
1 | # sklearn模型算法选择路径图 |
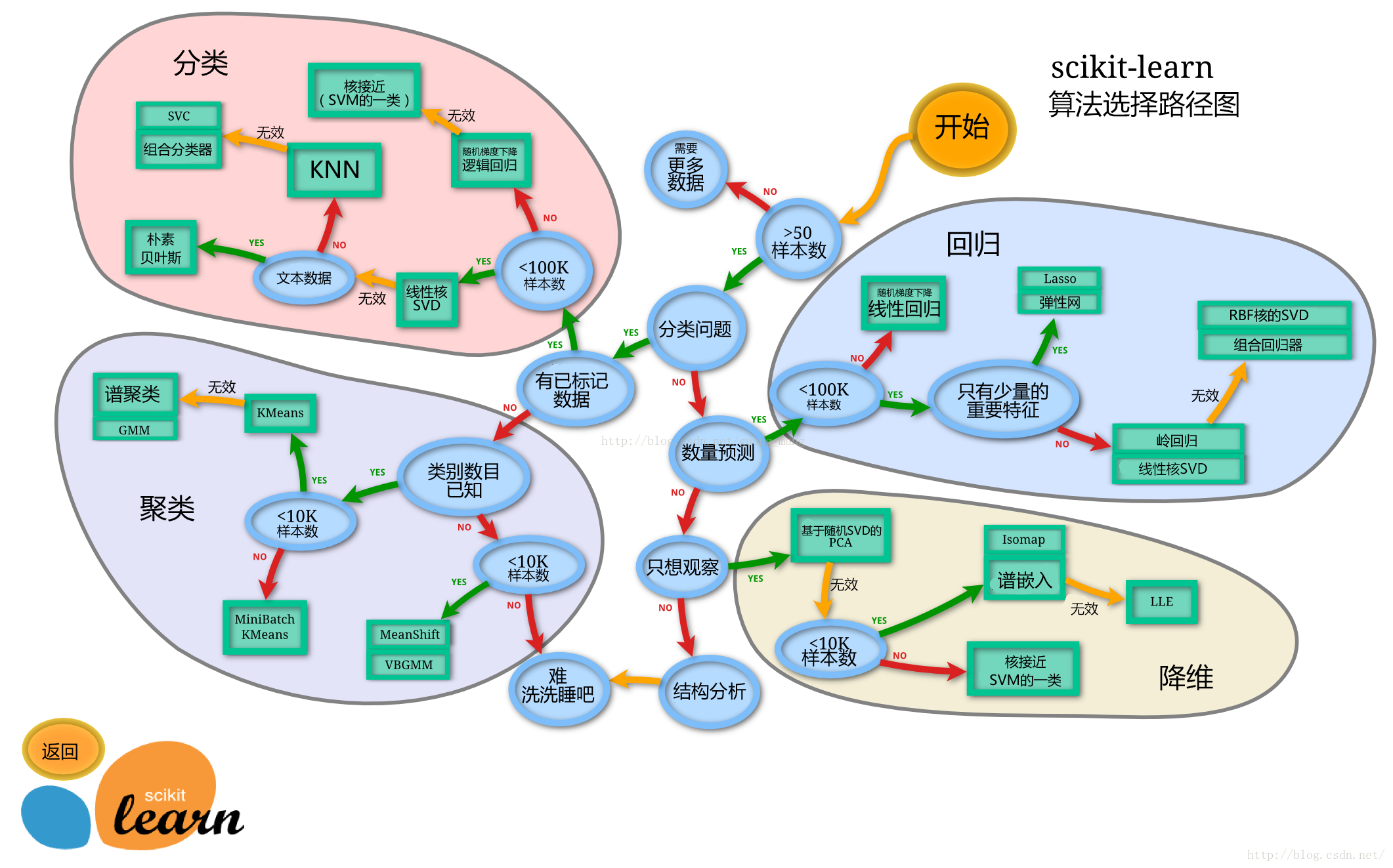
【思考】数据集哪些差异会导致模型在拟合数据是发生变化
1 | #思考回答 |
这里使用留出法划分数据集
【思考】 * 划分数据集的方法有哪些? * 为什么使用分层抽样,这样的好处有什么?
1 | # 划分数据集的方法有哪些? |
train_test_splittrain_test_split?后回车即可看到要从clear_data.csv和train.csv中提取train_test_split()所需的参数
1 | #写入代码 |
1 | #写入代码 |
((668, 11), (223, 11))【思考】 * 什么情况下切割数据集的时候不用进行随机选取
1 | #思考回答 |
LinearRegression混淆sklearn.linear_modelsklearn.ensemble1 | #写入代码 |
1 | #写入代码 |
/root/.pyenv/versions/3.11.1/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:465: ConvergenceWarning: lbfgs failed to converge (status=1):
STOP: TOTAL NO. OF ITERATIONS REACHED LIMIT.
Increase the number of iterations (max_iter) or scale the data as shown in:
https://scikit-learn.org/stable/modules/preprocessing.html
Please also refer to the documentation for alternative solver options:
https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression
n_iter_i = _check_optimize_result(1 | #写入代码 |
Training set score: 0.80
Testing set score: 0.791 | #写入代码 |
Training set score: 0.79
Testing set score: 0.78
/root/.pyenv/versions/3.11.1/lib/python3.11/site-packages/sklearn/linear_model/_logistic.py:465: ConvergenceWarning: lbfgs failed to converge (status=1):
STOP: TOTAL NO. OF ITERATIONS REACHED LIMIT.
Increase the number of iterations (max_iter) or scale the data as shown in:
https://scikit-learn.org/stable/modules/preprocessing.html
Please also refer to the documentation for alternative solver options:
https://scikit-learn.org/stable/modules/linear_model.html#logistic-regression
n_iter_i = _check_optimize_result(1 | # 默认参数的随机森林分类模型 |
Training set score: 1.00
Testing set score: 0.82【思考】 * 为什么线性模型可以进行分类任务,背后是怎么的数学关系 * 对于多分类问题,线性模型是怎么进行分类的
1 | #思考回答 |
predict能输出预测标签,predict_proba则可以输出标签概率1 | #写入代码 |
1 | #写入代码 |
array([0, 1, 1, 1, 0, 0, 1, 0, 1, 1])1 | #写入代码 |
1 | #写入代码 |
array([[0.60887905, 0.39112095],
[0.17668722, 0.82331278],
[0.40624596, 0.59375404],
[0.18896449, 0.81103551],
[0.87984221, 0.12015779],
[0.91385758, 0.08614242],
[0.13282516, 0.86717484],
[0.90555878, 0.09444122],
[0.05280619, 0.94719381],
[0.10934565, 0.89065435]])【思考】 * 预测标签的概率对我们有什么帮助
1 | #思考回答 |