橘子海
橘子海
橘子海,现场超超超超级赞,嗨到爆,完全超出预期
Give me the faith that we broke
请重拾我们背叛过的誓言
Reminds me the verse that we spoke
不要让我遗忘共同诵读过的诗篇
There is no chance for start it over
一切已经永远无法重来
Back to the check point be my lover
回不去那个你我还是“我们”的存盘点







橘子海,现场超超超超级赞,嗨到爆,完全超出预期
Give me the faith that we broke
请重拾我们背叛过的誓言
Reminds me the verse that we spoke
不要让我遗忘共同诵读过的诗篇
There is no chance for start it over
一切已经永远无法重来
Back to the check point be my lover
回不去那个你我还是“我们”的存盘点







技术栈:streamlit,fastapi,Gradio,langchain,dify,coze
列出所有环境conda env list
删除指定环境conda env remove –name 环境名称
创建 Conda 环境conda create -n llm-universe python==3.9.0
激活 Conda 环境conda activate llm-universe
安装依赖项pip install -r requirements.txt
10 分钟!零基础彻底学会 Cursor AI 编程 | Cursor AI 编程|Cursor 进阶技巧 | Cursor 开发小程序 | 小白 AI 编程_哔哩哔哩_bilibili
【Langchain进阶篇】12.Prompt templates Few shot. Example selector(提示模板:少镜头。示例选择器)_哔哩哔哩_bilibili
以下是 Hexo 常用的指令整理,方便快速查阅:
初始化博客
1
hexo init [文件夹名] # 创建新博客(不指定文件夹则在当前目录生成)
安装依赖
1 | npm install # 安装 Hexo 核心依赖(初始化后可能需要执行) |
本地预览
1 | hexo server # 启动本地服务器(默认端口 4000),缩写:hexo s |
生成静态文件
1 | hexo generate # 生成 public 文件夹的静态文件,缩写:hexo g |
部署到服务器
1
hexo deploy # 部署到 GitHub Pages 或其他平台,缩写:hexo d
新建文章
1
hexo new "文章标题" # 生成新文章(Markdown 文件),缩写:hexo n
新建页面
1
hexo new page "页面名" # 创建自定义页面(如 about、tags)
清理缓存
1
hexo clean # 删除生成的 public 和缓存文件(修改主题后建议执行)
查看帮助
1
hexo help # 查看所有指令说明
生成并部署
1
2hexo g -d # 先生成静态文件,再部署(等同 hexo generate && hexo deploy)
hexo d -g # 同上,顺序不影响结果
生成并预览
1
hexo s -g # 先生成文件,再启动本地服务器
_config.yml 中设置
deploy 参数(如 GitHub 仓库地址)。npm install hexo-deployer-git。themes/
文件夹后,在配置文件中指定主题名称。如果需要更详细的操作说明,可以补充具体场景(如更换主题、设置分类等)!
原因:Clash 虽然开启了代理,但 Git 默认不会走这个代理,导致连接 GitHub 时失败
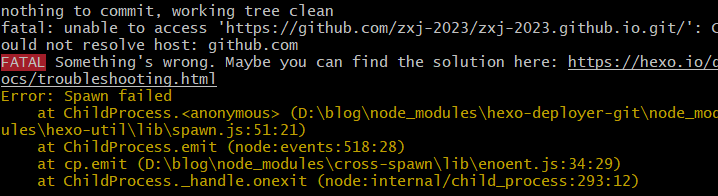
解决方案:
查看端口号
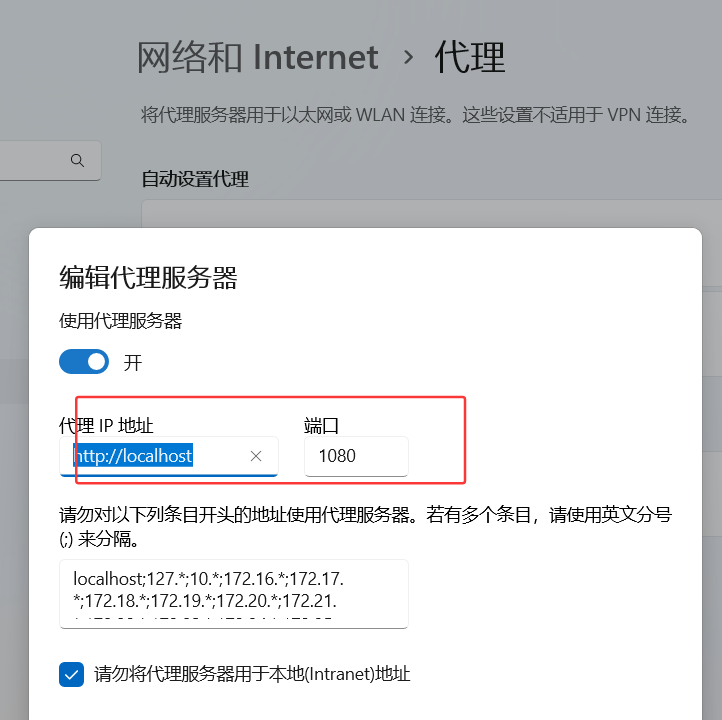
查看git代理
1 | git config --global --get http.proxy |
更改代理
1 | git config --global http.proxy socks5://127.0.0.1:1080 |
下面我将为你详细解释KKT(Karush-Kuhn-Tucker)条件。KKT条件是优化理论中用于求解带约束非线性规划问题的一组必要条件,广泛应用于支持向量机(SVM)等机器学习算法中。我会使用内联数学公式(如 f(x))来展示相关表达式。
我们考虑一个带有约束的优化问题,数学形式如下: - 目标:minxf(x) - 不等式约束:gi(x) ≤ 0,其中 i = 1, 2, …, m - 等式约束:hj(x) = 0,其中 j = 1, 2, …, p
这里: - f(x) 是目标函数,通常是我们希望最小化的函数。 - gi(x) ≤ 0 表示 m 个不等式约束。 - hj(x) = 0 表示 p 个等式约束。
KKT条件的目标是找到满足这些约束的局部最优解 x。
为了引入KKT条件,我们首先定义拉格朗日函数: $$\mathcal{L}(\mathbf{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = f(\mathbf{x}) + \sum_{i=1}^{m} \lambda_i g_i(\mathbf{x}) + \sum_{j=1}^{p} \mu_j h_j(\mathbf{x})$$
其中: - λ = (λ1, λ2, …, λm) 是与不等式约束 gi(x) ≤ 0 对应的拉格朗日乘子。 - μ = (μ1, μ2, …, μp) 是与等式约束 hj(x) = 0 对应的拉格朗日乘子。
拉格朗日函数将目标函数和约束条件结合在一起,通过引入乘子 λi 和 μj 来平衡约束对优化的影响。
KKT条件由以下四个部分组成,只有当某些正则性条件(如Slater条件)满足时,局部最优解 x 才会同时满足这些条件。以下是具体的KKT条件:
拉格朗日函数对 x 的梯度必须为零,即: $$\nabla_{\mathbf{x}} \mathcal{L}(\mathbf{x}, \boldsymbol{\lambda}, \boldsymbol{\mu}) = \nabla f(\mathbf{x}) + \sum_{i=1}^{m} \lambda_i \nabla g_i(\mathbf{x}) + \sum_{j=1}^{p} \mu_j \nabla h_j(\mathbf{x}) = 0$$
这意味着在最优解处,目标函数的梯度可以通过约束函数梯度的线性组合来表示。
解 x 必须满足原始问题的所有约束: - 不等式约束:gi(x) ≤ 0,其中 i = 1, 2, …, m - 等式约束:hj(x) = 0,其中 j = 1, 2, …, p
这确保了解仍在问题的可行域内。
对于不等式约束对应的拉格朗日乘子,必须满足: λi ≥ 0,其中 i = 1, 2, …, m
这表明不等式约束的乘子非负,反映了约束对优化方向的影响。
对于每个不等式约束,乘子与约束函数的乘积必须为零: λigi(x) = 0,其中 i = 1, 2, …, m
这意味着: - 如果某个约束不“紧”(即 gi(x) < 0),则对应的乘子 λi = 0。 - 如果 λi > 0,则该约束必须是“紧”的(即 gi(x) = 0)。
KKT条件在支持向量机(SVM)中尤为重要。SVM的原始优化问题为: - 目标:$$\min_{\mathbf{w}, b} \frac{1}{2} \|\mathbf{w}\|^2$$ - 约束:yi(w ⋅ xi + b) ≥ 1,其中 i = 1, 2, …, n
将其改写为标准形式的不等式约束:1 − yi(w ⋅ xi + b) ≤ 0。
拉格朗日函数为: $$\mathcal{L}(\mathbf{w}, b, \boldsymbol{\alpha}) = \frac{1}{2} \|\mathbf{w}\|^2 + \sum_{i=1}^{n} \alpha_i \left[ 1 - y_i (\mathbf{w} \cdot \mathbf{x}_i + b) \right]$$
应用KKT条件: 1. 梯度条件: - 对 w:$$\nabla_{\mathbf{w}} \mathcal{L} = \mathbf{w} - \sum_{i=1}^{n} \alpha_i y_i \mathbf{x}_i = 0$$ - 对 b:$$\frac{\partial \mathcal{L}}{\partial b} = -\sum_{i=1}^{n} \alpha_i y_i = 0$$ 2. 原始可行性:yi(w ⋅ xi + b) ≥ 1 3. 对偶可行性:αi ≥ 0 4. 互补松弛条件:αi[yi(w ⋅ xi + b) − 1] = 0
这些条件帮助我们识别支持向量(αi > 0 的点)并求解最优的 w 和 b。
KKT条件是求解带约束优化问题的核心工具,它通过梯度条件、原始可行性、对偶可行性和互补松弛条件,确保了解既是最优的,又满足所有约束。在机器学习中,KKT条件为SVM等算法提供了理论支持,是理解和实现这些模型的关键。

下面我们将推导支持向量机(SVM)中目标函数从原始问题转换为对偶问题的过程和条件,使用拉格朗日乘子法。我们将一步步展开,确保推导清晰且完整。
支持向量机(SVM)的目标是找到一个超平面,能够最大化到最近数据点的间隔。对于线性可分的情况,原始优化问题可以定义为:
目标函数:
$$\min_{\mathbf{w}, b} \frac{1}{2}
\|\mathbf{w}\|^2$$
约束条件:
yi(w ⋅ xi + b) ≥ 1, i = 1, 2, …, n
其中: - w 是超平面的法向量; - b 是超平面的截距; - xi 是训练样本,yi ∈ {−1, 1} 是对应的类别标签; - ∥w∥2 表示法向量的平方范数,目标是最小化它以最大化间隔; - 约束条件确保所有样本点被正确分类,并且到超平面的归一化距离至少为 1。
由于这是一个带不等式约束的优化问题,我们使用拉格朗日乘子法将其转换为无约束形式。引入拉格朗日乘子 α = (α1, α2, …, αn),其中 αi ≥ 0,构造拉格朗日函数:
$$\mathcal{L}(\mathbf{w}, b, \boldsymbol{\alpha}) = \frac{1}{2} \|\mathbf{w}\|^2 - \sum_{i=1}^{n} \alpha_i \left[ y_i (\mathbf{w} \cdot \mathbf{x}_i + b) - 1 \right]$$
我们的目标是通过拉格朗日函数,将原始问题转换为对偶问题。
对偶问题的核心思想是:先对 w 和 b 求拉格朗日函数的极小值,然后对 α 求极大值。即:
maxα ≥ 0minw, bℒ(w, b, α)
为了找到 ℒ 关于 w 和 b 的极小值,分别求偏导并令其为零:
对 w
求偏导:
$$\frac{\partial \mathcal{L}}{\partial
\mathbf{w}} = \mathbf{w} - \sum_{i=1}^{n} \alpha_i y_i \mathbf{x}_i =
0$$
解得:
$$\mathbf{w} = \sum_{i=1}^{n} \alpha_i y_i
\mathbf{x}_i$$
对 b 求偏导:
$$\frac{\partial \mathcal{L}}{\partial b} =
-\sum_{i=1}^{n} \alpha_i y_i = 0$$
解得:
$$\sum_{i=1}^{n} \alpha_i y_i =
0$$
这两个结果是后续推导的关键。
将 $$\mathbf{w} = \sum_{i=1}^{n} \alpha_i y_i \mathbf{x}_i$$ 代入拉格朗日函数,并利用 $$\sum_{i=1}^{n} \alpha_i y_i = 0$$ 简化:
$$\mathcal{L} = \frac{1}{2} \left\| \sum_{i=1}^{n} \alpha_i y_i \mathbf{x}_i \right\|^2 - \sum_{i=1}^{n} \alpha_i \left[ y_i \left( \left( \sum_{j=1}^{n} \alpha_j y_j \mathbf{x}_j \right) \cdot \mathbf{x}_i + b \right) - 1 \right]$$
计算第一项:
$$\left\| \sum_{i=1}^{n} \alpha_i y_i
\mathbf{x}_i \right\|^2 = \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i
\alpha_j y_i y_j (\mathbf{x}_i \cdot \mathbf{x}_j)$$
计算第二项中的内积部分:
$$y_i \left( \sum_{j=1}^{n} \alpha_j y_j
\mathbf{x}_j \right) \cdot \mathbf{x}_i = y_i \sum_{j=1}^{n} \alpha_j
y_j (\mathbf{x}_j \cdot \mathbf{x}_i)$$
所以:
$$\sum_{i=1}^{n} \alpha_i y_i \left(
\sum_{j=1}^{n} \alpha_j y_j (\mathbf{x}_j \cdot \mathbf{x}_i) \right) =
\sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j (\mathbf{x}_i
\cdot \mathbf{x}_j)$$
考虑 b 项:
$$\sum_{i=1}^{n} \alpha_i y_i b = b
\sum_{i=1}^{n} \alpha_i y_i = 0 \quad (\text{因为} \sum_{i=1}^{n}
\alpha_i y_i = 0)$$
代入后,拉格朗日函数变为:
$$\mathcal{L} = \frac{1}{2} \sum_{i=1}^{n}
\sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j (\mathbf{x}_i \cdot
\mathbf{x}_j) - \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j
(\mathbf{x}_i \cdot \mathbf{x}_j) + \sum_{i=1}^{n} \alpha_i$$
化简:
$$\mathcal{L} = -\frac{1}{2} \sum_{i=1}^{n}
\sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j (\mathbf{x}_i \cdot
\mathbf{x}_j) + \sum_{i=1}^{n} \alpha_i$$
于是,对偶问题是:
$$\max_{\boldsymbol{\alpha}} \left[
\sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n}
\alpha_i \alpha_j y_i y_j (\mathbf{x}_i \cdot \mathbf{x}_j)
\right]$$
为了与标准优化形式一致,常将其写为最小化问题:
$$\min_{\boldsymbol{\alpha}} \left[
\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j
(\mathbf{x}_i \cdot \mathbf{x}_j) - \sum_{i=1}^{n} \alpha_i
\right]$$
原始问题与对偶问题之间的关系由强对偶性保证。在SVM中: - 目标函数 $$\frac{1}{2} \|\mathbf{w}\|^2$$ 是凸函数(二次函数); - 约束条件 yi(w ⋅ xi + b) ≥ 1 是线性不等式; - 对于线性可分数据,Slater条件满足(存在可行解使约束严格成立)。
因此,强对偶性成立,原始问题的最优解可以通过对偶问题求解得到。
此外: - 最优的 α 通过对偶问题求解; - $$\mathbf{w} = \sum_{i=1}^{n} \alpha_i y_i \mathbf{x}_i$$; - 对于支持向量(αi > 0 的样本),yi(w ⋅ xi + b) = 1,可据此解出 b。
原始问题:
$$\min_{\mathbf{w}, b} \frac{1}{2}
\|\mathbf{w}\|^2$$
受约束:yi(w ⋅ xi + b) ≥ 1
对偶问题:
$$\max_{\boldsymbol{\alpha}} \left[
\sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n}
\alpha_i \alpha_j y_i y_j (\mathbf{x}_i \cdot \mathbf{x}_j)
\right]$$
受约束:$$\sum_{i=1}^{n} \alpha_i y_i =
0$$,αi ≥ 0
转换条件:
通过拉格朗日乘子法,基于凸优化和强对偶性完成转换。对偶形式不仅便于求解,还为引入核函数奠定了基础。
以上就是SVM目标函数从原始问题到对偶问题的推导过程和条件。

在这张图片中,表格列出了 x 和 y
的十六进制值,并且要求用 C
语言中的位运算符对它们进行操作。接下来,我将对每个表达式进行详细的计算和解释。
在表格中,要求使用 C 语言中的不同位运算符来计算 x 和
y 之间的结果。位运算符包括:
&(位与)|(位或)^(位异或)~(位取反)<<(左移)>>(右移)!(逻辑非)x & y: 位与运算会比较
x 和 y 的每一位,只有当对应位都为 1
时,结果才为 1,否则为 0。x | y: 位或运算会比较
x 和 y 的每一位,只要对应位有一个为
1,结果就为 1。x ^ y: 位异或运算会比较
x 和 y 的每一位,当两者相同时,结果为
0;当两者不同时,结果为 1。~x 和 ~y:
位取反运算会将 x 或 y 的每一位都反转,0 变
1,1 变 0。x << y: 左移运算会将
x 的二进制位向左移动 y 位,并在右边补 0。x >> y: 右移运算会将
x 的二进制位向右移动 y
位,符号位(对于负数来说是 1)保持不变。!x: 逻辑非运算对
x 进行布尔值判断,如果 x 为 0,则结果为
1,否则为 0。核心原理: 每一个十六进制数字正好对应 4 个二进制位。这是因为 16=24。
我们可以将十六进制数 8080 108B H
中的每一位数字,分别转换为它对应的4位二进制数:
8 H =
1000 b0 H =
0000 b8 H =
1000 b0 H =
0000 b1 H =
0001 b0 H =
0000 b8 H =
1000 bB H (B 代表十进制的 11) =
1011 b组合: 现在,按照原始十六进制数的顺序,把这些4位的二进制数组合起来:
1000 (来自8) + 0000
(来自0) + 1000 (来自8) +
0000 (来自0) + 0001
(来自1) + 0000 (来自0) +
1000 (来自8) + 1011
(来自B)
结果: 将它们连接在一起就得到:
1000 0000 1000 0000 0001 0000 1000 1011 b
所以,8080 108B H 等于
1000 0000 1000 0000 0001 0000 1000 1011 b
是因为每个十六进制位都可以独立地、直接地转换为一个4位的二进制表示,然后按顺序拼接起来。
好的,我们来详细解释一下为什么在不同的指令下,寄存器 R1 和 R2 的内容
0000 108B H 和 8080 108B H
会对应不同的真值。核心原因在于,指令决定了如何解释寄存器中的二进制位串。
(1)无符号数加法指令 (Unsigned Addition)
(2)带符号整数乘法指令 (Signed Integer Multiplication)
解释规则:
当执行带符号整数指令时,计算机会使用
补码 (Two’s Complement)
来表示整数。
0 代表正数或零,1 代表负数。(3)单精度浮点数减法指令 (Single-Precision Floating-Point Subtraction)
解释规则:
当执行浮点数指令时,计算机会按照
IEEE 754 单精度 (32位)
标准来解释寄存器中的位。格式如下:
0
为正,1 为负。e + bias,其中 e 是实际指数,bias
(偏移量) 对于单精度是 127。1.F(有一个隐藏的1)。在开始计算之前,我们先了解补码的基本规则:
0U 后面的 U
确实表示无符号的意思。具体来说:0
本身:这是一个整数常量,默认情况下是有符号整数类型(signed int)。0U 的含义:当在 0
后面加上 U
后缀时,它就变成了一个无符号整数常量(unsigned int)。U
后缀明确指定了这个数字是无符号类型。在 C 语言中,可以通过后缀来指定整数常量的类型: -
无后缀:表示默认的有符号整数(int)。 -
U 或
u:表示无符号整数(unsigned int)。 -
L 或
l:表示长整型(long int)。 -
UL 或
ul:表示无符号长整型(unsigned long int)。
0:有符号整数,值是 0。0U:无符号整数,值仍然是 0,但它的类型是
unsigned int。无符号类型和有符号类型的区别在某些情况下会影响程序的行为,比如比较运算: - 如果比较两个无符号整数,或者两个有符号整数,直接按数值比较即可。 - 如果一个是有符号整数,另一个是无符号整数,C 语言会将有符号整数转换为无符号整数后再比较。这可能导致意外结果,例如负数在转换为无符号整数时变成一个很大的正数。
总之,U
后缀的作用就是告诉编译器,这个整数常量是无符号的。所以你的理解是对的,后面带
U 就是无符号的意思!
(unsigned) -1 > -2 中,-1
被转换为无符号整数,而 -2 也被按无符号数处理。(unsigned) -1
的含义-1
从有符号整数(int)转换为无符号整数(unsigned int)。-1 的补码是 1111...1111(32
位全 1)。1111...1111 作为无符号整数的值是 (2^{32} - 1 =
4294967295)。(unsigned) -1 的结果是
4294967295。-2
为什么按无符号数处理(unsigned) -1 > -2 中,-2
默认是一个有符号整数(int),其补码表示为
1111...1110(32 位中最后一位是 0)。(unsigned) -1)与一个有符号整数(-2)进行比较时,C
语言会执行隐式类型转换,以确保两个操作数的类型一致。-2 会被隐式转换为无符号整数:
1111...1110 作为无符号整数的值是 (2^{32} - 2 =
4294967294)。(unsigned) -1 > -2 变成了:
(unsigned) -1 = 4294967295(无符号整数)。-2 被转换为
4294967294(无符号整数)。4294967295 > 4294967294,显然成立,结果为真(1)。-2
被按无符号数处理-2 被按无符号数处理的原因在于 C
语言的类型转换规则:
(unsigned) -1 强制指定了无符号类型。-2 由于与无符号数比较,被隐式转换成了无符号数。-1
显式转换为无符号整数,结果是 4294967295。4294967294。-2
被按无符号数处理。这种机制虽然确保了类型一致性,但在处理负数时可能导致意外结果,因此在使用无符号类型时需要特别注意。希望这个解释清晰地回答了你的问题!
1 | import numpy as np |
1 | data = pd.read_csv("work/西瓜数据集3.0α.txt") |
1 | yes = data[data['Good melon'].isin(['是'])] |
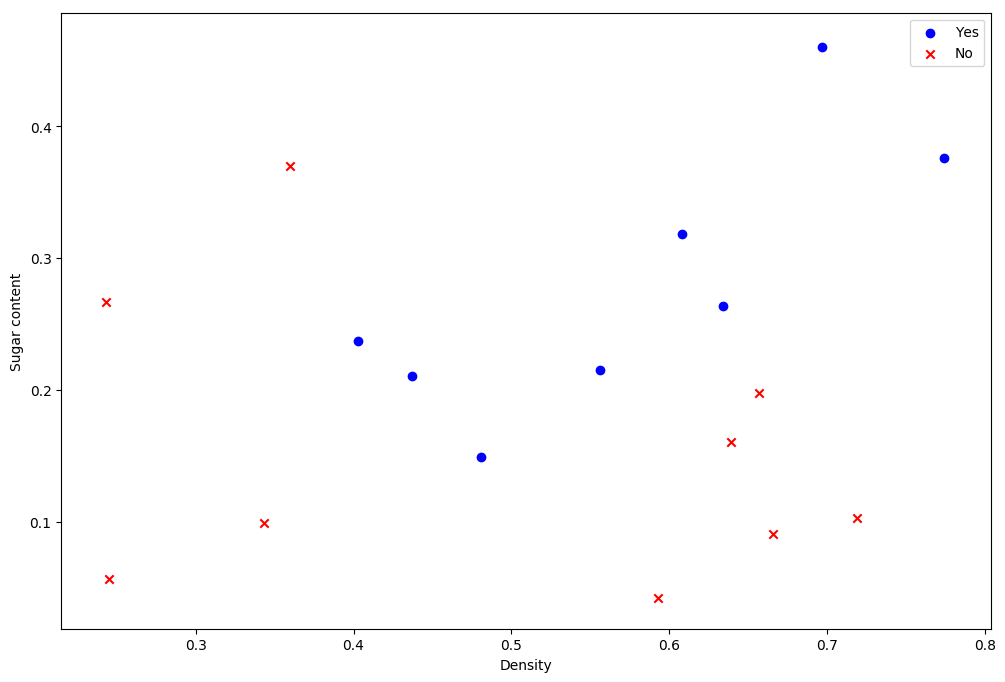
在SVM分类器中,使用线性核与高斯核进行比较。
1 | from sklearn import svm |
1 | temp = {'是': 1, '否': -1} |
1 | linear_svc.fit(X, y) |
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/sklearn/utils/validation.py:760: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
y = column_or_1d(y, warn=True)
array([[0.666, 0.091],
[0.243, 0.267],
[0.343, 0.099],
[0.639, 0.161],
[0.657, 0.198],
[0.36 , 0.37 ],
[0.593, 0.042],
[0.719, 0.103],
[0.697, 0.46 ],
[0.774, 0.376],
[0.634, 0.264],
[0.608, 0.318],
[0.556, 0.215],
[0.403, 0.237],
[0.481, 0.149],
[0.437, 0.211]])1 | rbf_svc.fit(X, y) |
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/sklearn/utils/validation.py:760: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
y = column_or_1d(y, warn=True)
array([[0.666, 0.091],
[0.243, 0.267],
[0.245, 0.057],
[0.343, 0.099],
[0.639, 0.161],
[0.657, 0.198],
[0.36 , 0.37 ],
[0.593, 0.042],
[0.719, 0.103],
[0.697, 0.46 ],
[0.774, 0.376],
[0.634, 0.264],
[0.608, 0.318],
[0.556, 0.215],
[0.403, 0.237],
[0.481, 0.149],
[0.437, 0.211]])将原始的Logistic Regression 进行核化,使用不同的核函数进行比较。
1 |
|
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/ipykernel_launcher.py:97: RuntimeWarning: overflow encountered in exp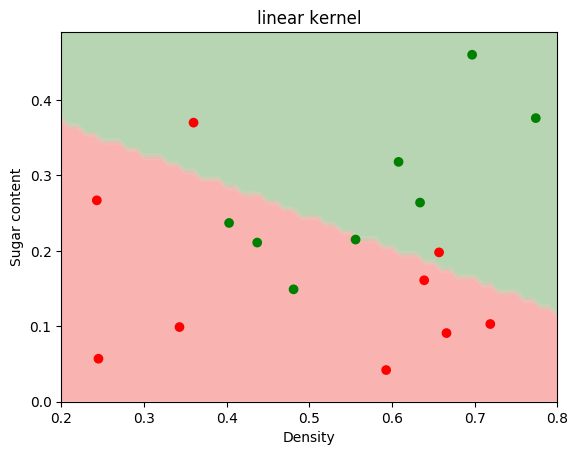
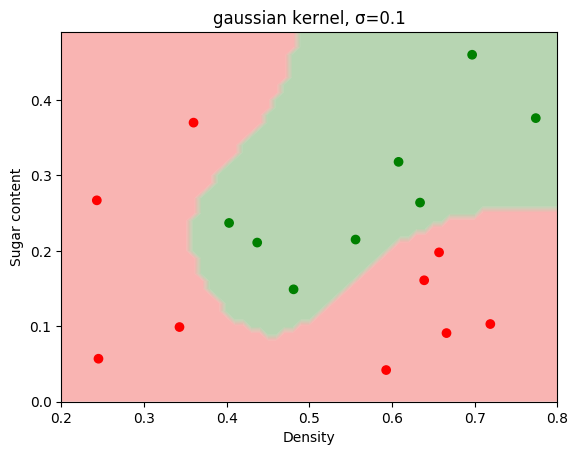
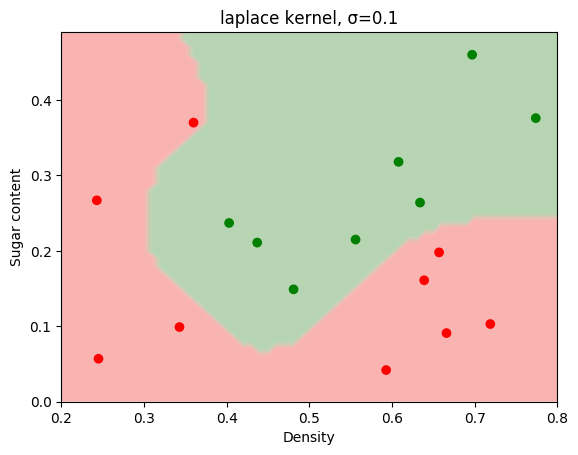
γ 控制影响范围:γ
越大,局部性越强(对邻近点更敏感)。以下是欧氏距离(Euclidean Distance)与曼哈顿距离(Manhattan Distance)的详细对比:
| 距离类型 | 公式 | 几何意义 |
|---|---|---|
| 欧氏距离 | ( |x - y|_2 = ) | 两点之间的直线距离 |
| 曼哈顿距离 | ( |x - y|1 = {i=1}^n | x_i - y_i |
假设两点 ( A(1, 1) ) 和 ( B(4, 5) ):
| 特征名称 | 特征含义 | 取值举例 |
|---|---|---|
| feature1 | 怀孕次数 | 6 |
| feature2 | 2小时口服葡萄糖耐受实验中的血浆葡萄浓度 | 148 |
| feature3 | 舒张压 (mm Hg) | 72 |
| feature4 | 三头肌皮褶厚度(mm) | 35 |
| feature5 | 2小时血清胰岛素浓度 (mu U/ml) | 0 |
| feature6 | 体重指数(weight in kg/(height in m)^2) | 33.6 |
| feature7 | 糖尿病谱系功能(Diabetes pedigree function) | 0.627 |
| feature8 | 年龄 | 50 |
| class | 是否患有糖尿病 | 1:阳性;0:阴性 |
主要任务如下: - 请先将数据使用sklearn中的StandardScaler进行标准化; - 然后使用sklearn中的svm.SVC支持向量分类器,构建支持向量机模型(所有参数使用默认参数),对测试集进行预测,将预测结果存为pred_y,并对模型进行评价; - 最后新建一个svm.SVC实例clf_new,并设置惩罚系数C=0.3,并利用该支持向量分类器对测试集进行预测,将预测结果存为pred_y_new,并比较两个模型的预测效果。
待补全代码
1 | import pandas as pd |
[187 180]
precision recall f1-score support
0 0.82 0.90 0.86 107
1 0.70 0.55 0.62 47
accuracy 0.79 154
macro avg 0.76 0.73 0.74 154
weighted avg 0.78 0.79 0.78 154
[197 196]
precision recall f1-score support
0 0.83 0.92 0.87 107
1 0.75 0.57 0.65 47
accuracy 0.81 154
macro avg 0.79 0.75 0.76 154
weighted avg 0.81 0.81 0.80 154
预期结果
在支持向量分类器中,核函数对其性能有直接的影响。已知径向基函数 RBF 及核矩阵元素为: K(xi, xj) = exp (−γ∥xi − xj∥2) 且对于核矩阵K,有Kij = K(xi, xj).
主要任务如下: - 自定义函数实现径向基函数 rbf_kernel,要求输入参数为两个矩阵 X、Y,以及 gamma; - 利用rbf_kernel核函数,计算标准化后的训练集scaled_train_X的核矩阵,并存为 rbf_matrix; - 利用rbf_kernel核函数,训练支持向量分类器 clf,并预测标准化后的测试数据 scaled_test_X 的标签,最后评价模型效果。 > 提示:先计算各自的 Gram 矩阵,然后再使用 np.diag 提取对角线元素,使用 np.tile 将列表扩展成一个矩阵。
待补全代码
1 | import numpy as np |
[250 208]
precision recall f1-score support
0 0.84 0.89 0.86 107
1 0.71 0.62 0.66 47
accuracy 0.81 154
macro avg 0.77 0.75 0.76 154
weighted avg 0.80 0.81 0.80 154预期结果
主要任务如下: - 读取sklearn中的iris数据集,提取特征与标记,并进行数据划分为训练与测试集; - 自定义函数实现SVM; - 调用SVM函数进行支持向量机训练,并对测试集进行测试。
待补全代码
1 | import numpy as np |
1 | class SVM: |
1 | # 调用SVM进行模型训练与测试评估 |
0.921 |
待补全代码
1 | import numpy as np |
[[0.94321144]
[1.83125284]
[4.71149329]]1.感知机是根据输入实例的特征向量x对其进行二类分类的线性分类模型:
f(x) = sign (w ⋅ x + b)
感知机模型对应于输入空间(特征空间)中的分离超平面w ⋅ x + b = 0。
2.感知机学习的策略是极小化损失函数:
minw, bL(w, b) = −∑xi ∈ Myi(w ⋅ xi + b)
损失函数对应于误分类点到分离超平面的总距离。
3.感知机学习算法是基于随机梯度下降法的对损失函数的最优化算法,有原始形式和对偶形式。算法简单且易于实现。原始形式中,首先任意选取一个超平面,然后用梯度下降法不断极小化目标函数。在这个过程中一次随机选取一个误分类点使其梯度下降。
4.当训练数据集线性可分时,感知机学习算法是收敛的。感知机算法在训练数据集上的误分类次数k满足不等式:
$$ k \leqslant\left(\frac{R}{\gamma}\right)^{2} $$
当训练数据集线性可分时,感知机学习算法存在无穷多个解,其解由于不同的初值或不同的迭代顺序而可能有所不同。
随机抽取一个误分类点使其梯度下降。
w = w + ηyixi
b = b + ηyi
当实例点被误分类,即位于分离超平面的错误侧,则调整w, b的值,使分离超平面向该无分类点的一侧移动,直至误分类点被正确分类。
使用iris数据集中两个类别的数据和[sepal length,sepal width]作为特征,进行感知机分类。
1 | import pandas as pd |
<matplotlib.legend.Legend at 0x7f177628f110>
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/font_manager.py:1331: UserWarning: findfont: Font family ['sans-serif'] not found. Falling back to DejaVu Sans
(prop.get_family(), self.defaultFamily[fontext]))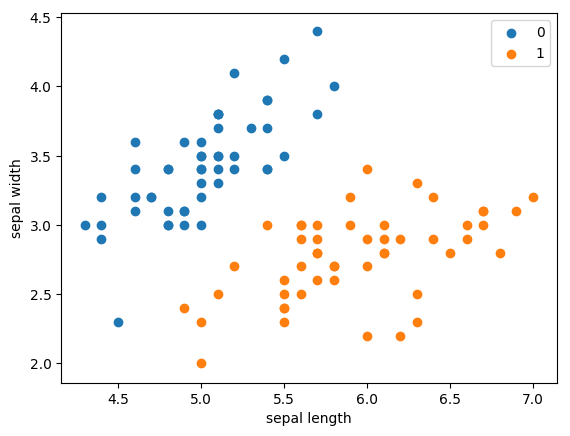
待补全代码
1 | # 数据线性可分,二分类数据 |
1 | # 进行模型训练 |
<matplotlib.legend.Legend at 0x7f1773a0c950>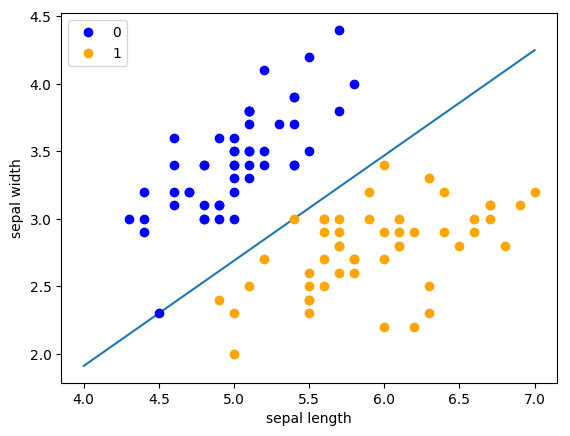
1 | import sklearn |
[[ 1.16 -1.935]]
[-0.25]1 | # 画布大小 |
<matplotlib.legend.Legend at 0x7f1769a4eb50>
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/font_manager.py:1331: UserWarning: findfont: Font family ['sans-serif'] not found. Falling back to DejaVu Sans
(prop.get_family(), self.defaultFamily[fontext]))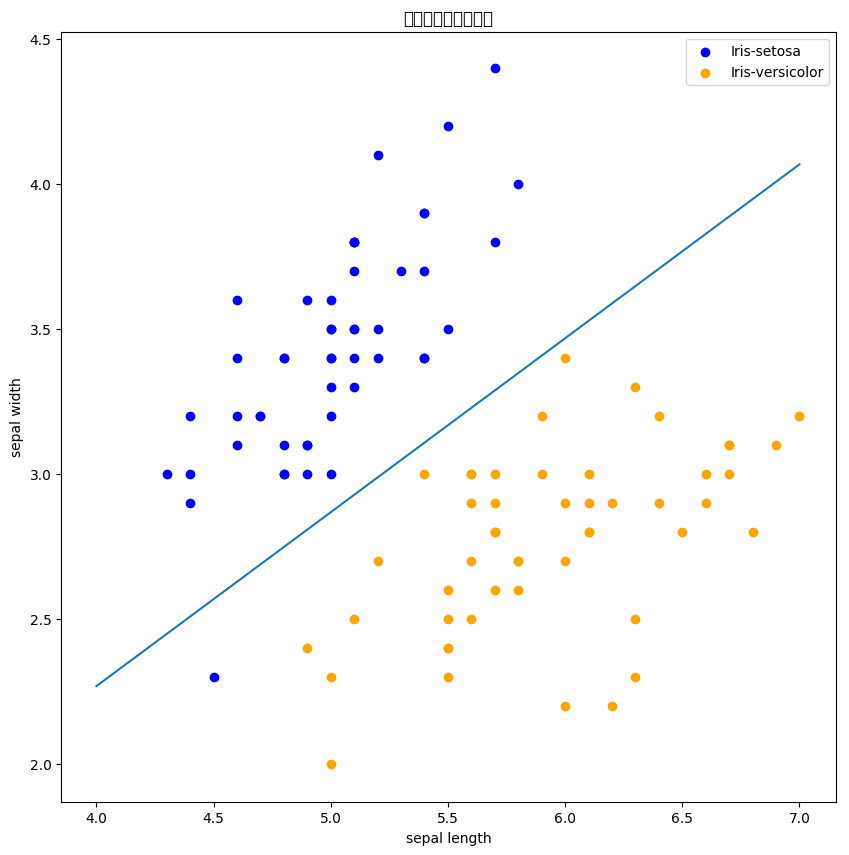
1 | import numpy as np |
特征权重 (w): [[0. 0.]]
截距 (b): [0.]
预测结果: [-1 -1 -1 -1]
真实标签: [ 1 1 -1 -1]
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/font_manager.py:1331: UserWarning: findfont: Font family ['sans-serif'] not found. Falling back to DejaVu Sans
(prop.get_family(), self.defaultFamily[fontext]))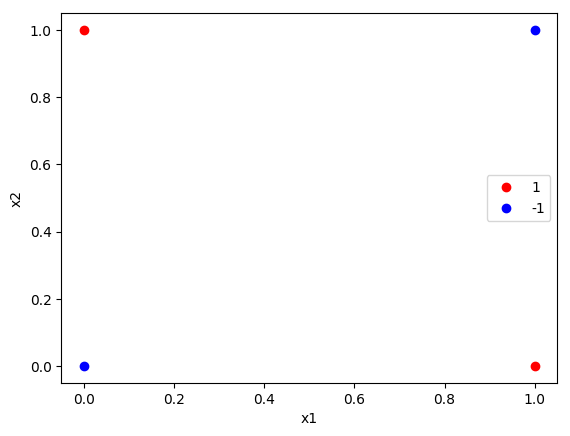
类别不均衡(Class Imbalance)
是指分类任务中不同类别样本的数量差异显著,例如:
- 多数类(Majority
Class):样本数量多(如正常交易占99%)。
- 少数类(Minority
Class):样本数量极少(如欺诈交易仅占1%)。
这种问题会导致模型倾向于预测多数类,严重降低少数类的预测性能(如漏检欺诈行为)。以下是详细解释和解决方案:
1. 类别不均衡的影响
2. 解决方案
2.1 数据层面调整
2.2 算法层面调整
class_weight='balanced'),让模型更关注少数类。2.3 评估指标调整
2.4 高级技术
异常检测(Anomaly Detection)
将少数类视为异常,使用 One-Class SVM 或孤立森林(Isolation
Forest)检测。
生成对抗网络(GAN)
使用 GAN 生成高质量的少数类样本(如医疗数据中的罕见病样本)。
阈值调整
根据业务需求调整分类阈值(如将欺诈检测的阈值从 0.5 降低到
0.3)。
3. 实际应用建议
imbalanced-learn(提供 SMOTE、EasyEnsemble
等)。class_weight 参数。总结
类别不均衡的核心是让模型“看到”足够的少数类信息,同时选择合适的评估指标。根据数据特点和业务需求,灵活组合数据采样、算法改进和评估方法,才能有效提升模型对少数类的识别能力。
以下是误差逆传播(Backpropagation, BP)算法中误差 ( E_k ) 对权重 ( w_{hj} )(输出层权重)和 ( v_{ih} )(隐藏层权重)的详细导数推导过程:
符号定义
1. 计算 ( $ $)(输出层权重的梯度)
步骤分解:
输出层输入:
[ $net_j = \sum_{h=1}^q w_{hj} b_h$ ]
输出层节点的激活值为 ( yj = f(netj)
)。
损失函数对 ( net_j ) 的导数:
[ $\frac{\partial E_k}{\partial net_j} =
\frac{\partial E_k}{\partial y_j} \cdot \frac{\partial y_j}{\partial
net_j}$ ]
损失函数对 ( w_{hj} ) 的导数:
[ $\frac{\partial E_k}{\partial w_{hj}} =
\frac{\partial E_k}{\partial net_j} \cdot \frac{\partial net_j}{\partial
w_{hj}}$ ]
2. 计算 ( $ $)(隐藏层权重的梯度)
步骤分解:
1. 隐藏层输入:
[ $net_h = \sum_{i=1}^n v_{ih} x_i$ ]
隐藏层节点的激活值为 ($ b_h = f(net_h) $)。
3. 最终梯度公式
输出层权重梯度:
[ $\frac{\partial E_k}{\partial w_{hj}} =
\delta_j \cdot b_h, \quad \text{其中 } \delta_j = (y_j - \hat{y}_j)
\cdot y_j (1 - y_j)$ ]
隐藏层权重梯度:
[ $\frac{\partial E_k}{\partial v_{ih}} =
\delta_h \cdot x_i, \quad \text{其中 } \delta_h = \left( \sum_{j=1}^l
\delta_j \cdot w_{hj} \right) \cdot b_h (1 - b_h)$ ]
4. 参数更新规则
使用梯度下降法更新权重:
1. 输出层权重更新:
[ $w_{hj} \leftarrow w_{hj} - \eta \cdot
\frac{\partial E_k}{\partial w_{hj}}$ ]
关键点总结
如果需要进一步解释具体步骤或示例,请随时告诉我! 😊
现有一个数据集 weekend.txt,目标是根据一个人的特征来预测其周末是否出行。
所有特征均为二元特征,取值为 0 或 1,其中“status”(目标特征也是类别)表示用户的周末是否出行,1 表示出行,0 表示不出行,“marriageStatus”表示申请人是否已婚、“hasChild”表示申请人是否有小孩、“hasAppointment”表示申请人是否有约、“weather”表示天气是否晴朗。
已知信息熵和信息增益的公式为:
$$\text{Entropy}(D)=-\sum_{k=1}^{C}p_k \cdot log_2(p_k)$$
$$\text{InfoGain}(D, a)=\text{Entropy}(D)-\sum_{v=1}^{V}\frac{|D^v|}{|D|} \cdot\text{Entropy}(D^v)$$
请完成以下三个内容:
请自定义函数 cal_entropy(data, feature_name)计算数据集data关于feature_name的信息熵。输入参数 data 为 DataFrame,feature_name 为目标特征(或类别)的名称;
请调用 cal_entropy() 函数计算决策树分支之前的信息熵,保存为 data_entropy;
请自定义函数 cal_infoGain(data, base_entropy) 计算 weekend.txt 中各个特征的信息增益,保存为列表 infogains,并选择信息增益最大的分支节点 best_feature。
补全代码
1 | # 导入必要库 |
各特征的信息增益: [0.0076, 0.0076, 0.0322, 0.0868]
信息增益最大的特征: weather期望输出:
现在有一份有关商品销量的数据集product.csv,数据集的离散型特征信息如下:
| 特征名称 | 取值说明 |
|---|---|
| 天气 | 1:天气好;0:天气坏 |
| 是否周末 | 1:是;0:不是 |
| 是否有促销 | 1:有促销;0:没有促销 |
| 销量 | 1:销量高;0:销量低 |
请完成以下三个内容: - 请根据提供的商品销量数据集 data,使用 sklearn 中的 DecisionTreeClassifier()函数构建决策树模型,模型选择分支结点的特征以Gini指数为判定准则; - 训练模型,并对测试集test_X进行预测,将预测结果存为 pred_y,进行模型评估; - 将构建的决策树模型进行可视化。
补全代码
1 | import pandas as pd |
模型分类报告:
precision recall f1-score support
0 1.00 0.50 0.67 2
1 0.67 1.00 0.80 2
accuracy 0.75 4
macro avg 0.83 0.75 0.73 4
weighted avg 0.83 0.75 0.73 4
期望输出:

1 | import numpy as np |
1 |