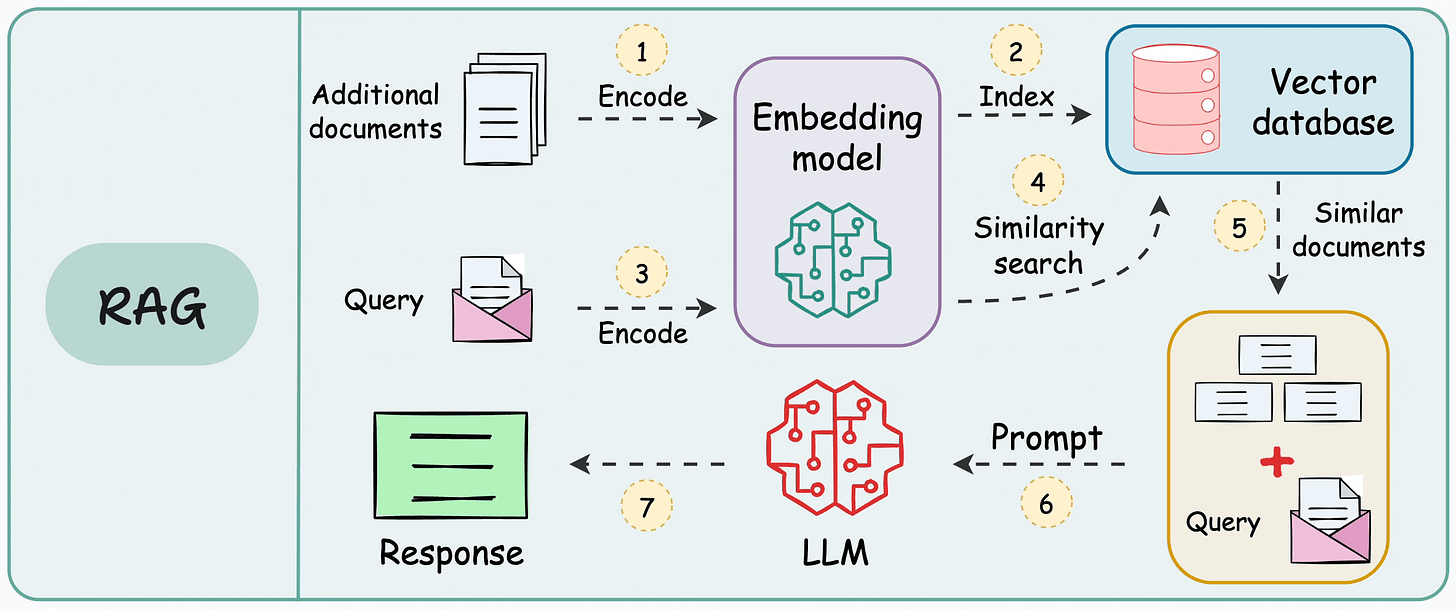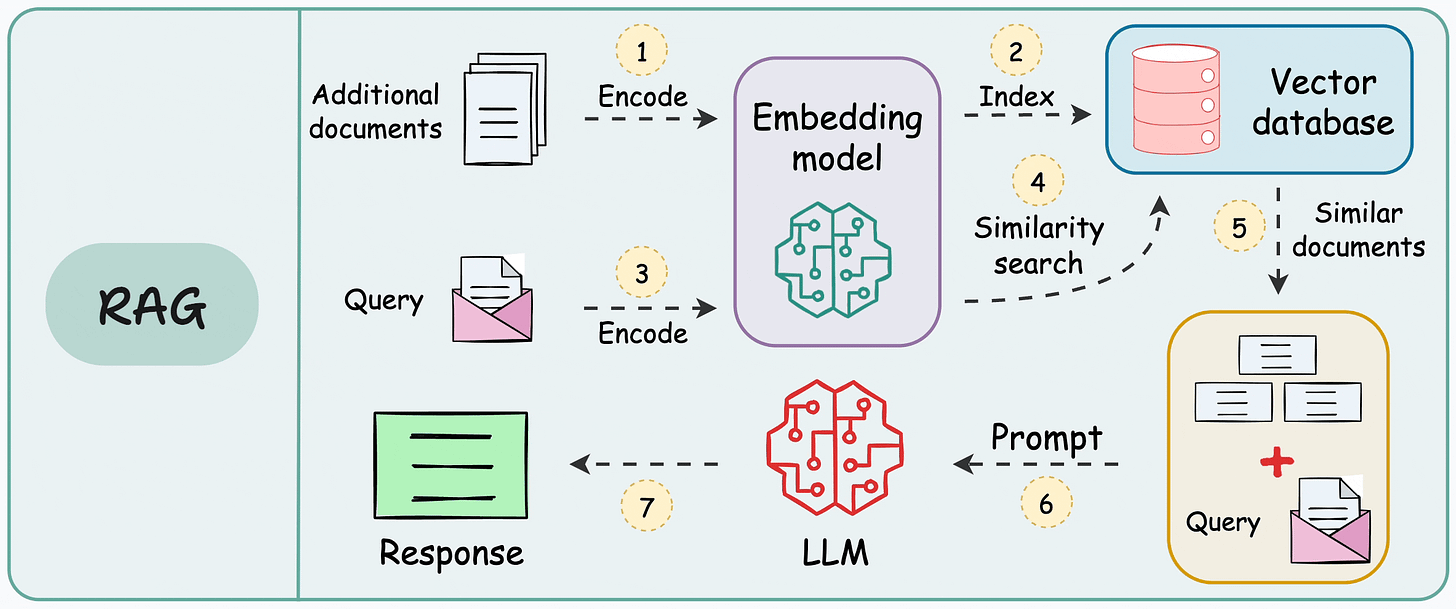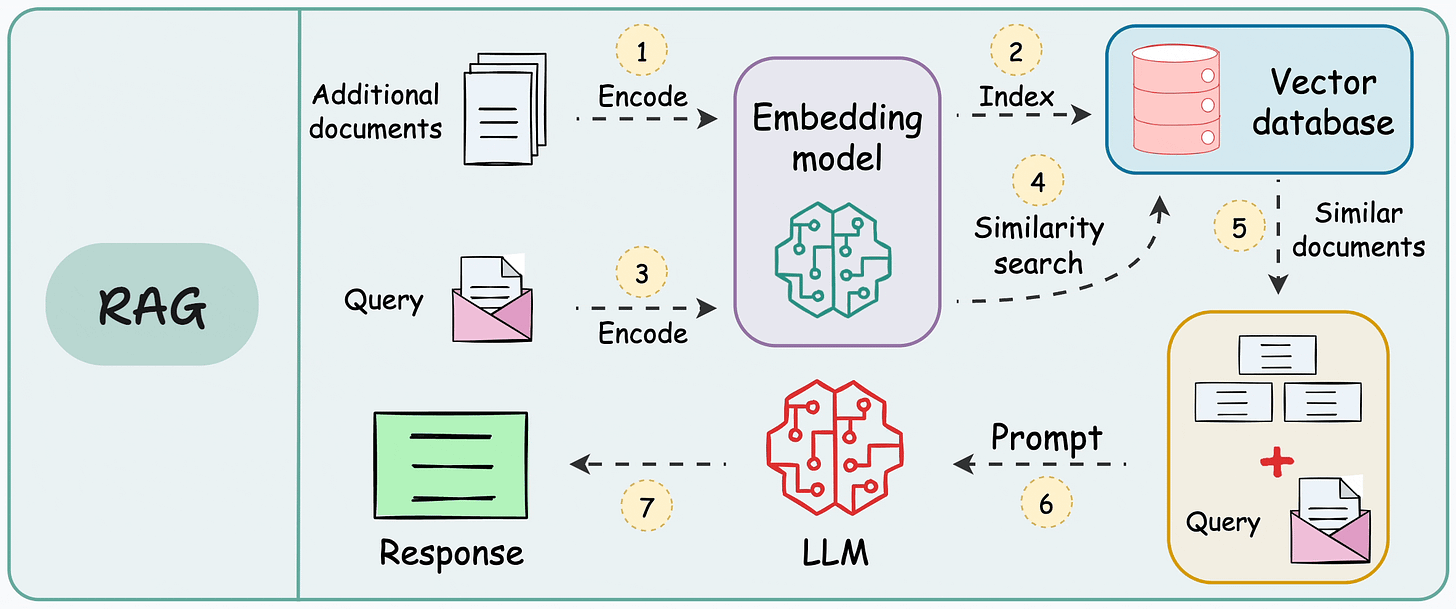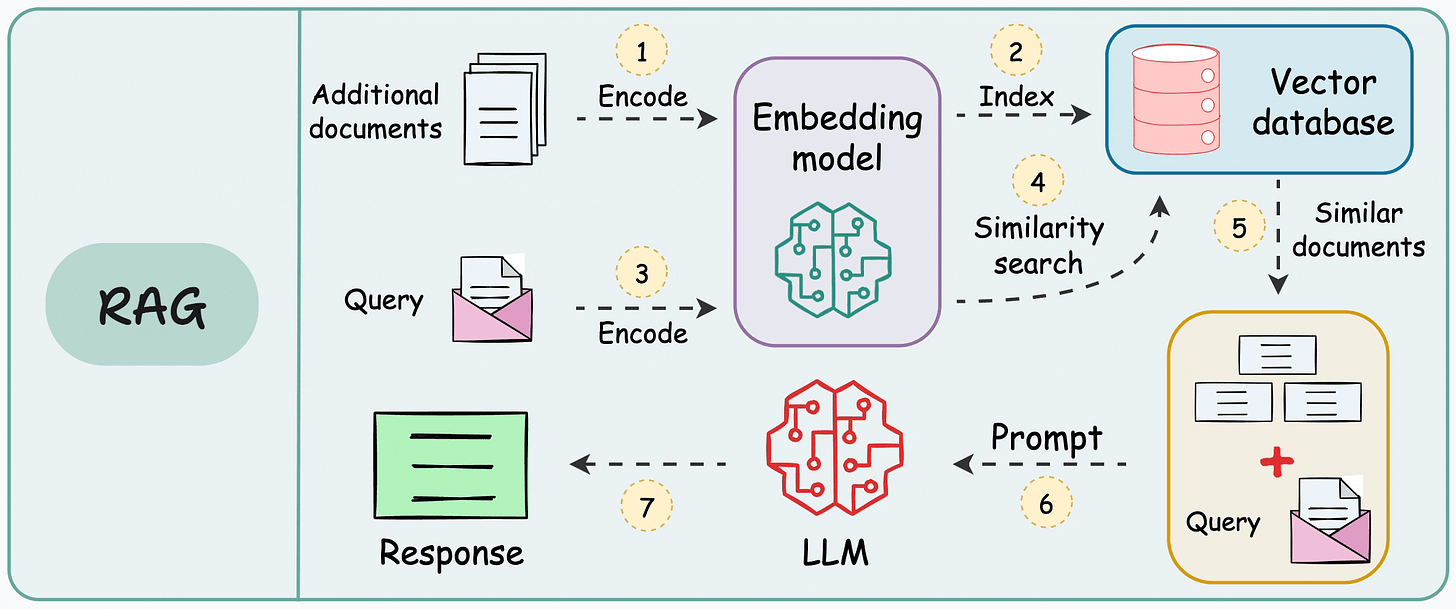
rag与检索评估
rag评估的指标
忠诚度Faithfulness
Faithfulness:衡量生成答案与给定上下文之间的事实一致性。忠实度得分是基于答案和检索到的上下文 计算出来的,答案的评分范围在0到1之间,分数越高越好。
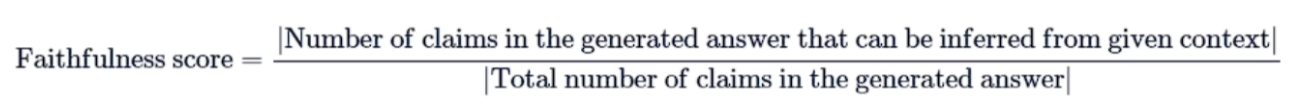
计算方式:将大模型给出的答案进行切片,检索给出的上下文,计算这些切片是否在上下文中

答案相关性Answerrelevance
Answerrelevance:答案相关性的评估指标旨在评估生成的答案与给定提示的相关程度。如果答案不完 整或包含冗余信息,则会被赋予较低的分数。这个指标使用问题和答案来计算,其值介于0到1之间,得 分越高表明答案的相关性越好

计算方式:根据答案生成多个问题,然后计算生成的答案与原答案的余弦相似度,再取平均

上下文精确度ContextPrecision
ContextPrecision:上下文精确度衡量上下文中所有相关的真实信息是否被排在了较高的位置。理想情 况下,所有相关的信息块都应该出现在排名的最前面。这个指标是根据问题和上下文来计算的,数值范 围在0到1之间,分数越高表示精确度越好。 $$ \text{Context Precision} = \frac{\sum_{k=1}^{K} (\text{rel}(k) \times \frac{\text{Precision@k}}{\text{Ideal Precision@k}})}{\text{Total Relevant Documents}} $$
K:检索返回的文档总数(如 top-5)rel(k):第k个文档是否相关(相关=1,无关=0)Precision@k:前k个文档的精确率(相关文档数 / k)Ideal Precision@k:理想情况下前k个文档的精确率(假设所有相关文档都排在最前面)
上下文召回率ContextRecall
ContextRecall:用来衡量检索到的上下文与被视为事实真相的标注答案的一致性程度。它根据事实真相 和检索到的上下文来计算,数值范围在0到1之间,数值越高表示性能越好。 为了从事实真相的答案中估计上下文召回率,需要分析答案中的每个句子是否可以归因于检索到的 上下文。在理想情况下,事实真相答案中的所有句子都应该能够对应到检索到的上下文中。 $$ \text{Context Recall} = \frac{|\{\text{返回的相关文档}\} \cap \{\text{标准相关文档}\}|}{|\{\text{标准相关文档}\}|} $$ 计算方式:上下文是否包括了标准答案的内容
检索性能的评估
平均倒数排名(Mean Reciprocal Rank, MRR)
平均倒数排名(Mean Reciprocal Rank, MRR) 是一种常用于评估信息检索系统、推荐系统或问答系统性能的评价指标。它特别适用于“每个查询只有一个正确答案”或“我们只关心第一个正确结果”的场景。
倒数排名(Reciprocal Rank, RR):对于一个查询,如果第一个正确答案出现在排序结果的第 $ k $ 位,那么它的倒数排名为: $$ RR = \frac{1}{k} $$ 如果没有正确答案,则 $ RR = 0 $。
平均倒数排名(MRR):对多个查询的倒数排名取平均值: $$ MRR = \frac{1}{|Q|} \sum_{i=1}^{|Q|} \frac{1}{\text{rank}_i} $$ 其中:
- $ |Q| $ 是查询的总数,
- $ _i $ 是第 $ i $ 个查询中第一个正确答案的排名(位置)。

平均精确率均值(Mean Average Precision, MAP)
MAP(Mean Average Precision) 是对多个查询或样本的 平均精确率(Average Precision, AP) 取平均,用来衡量排序结果的相关性质量。它综合考虑了:
- 排序中相关结果的数量(召回)
- 相关结果在排序中的位置(越靠前越好)
平均精确率(Average Precision, AP)
AP 是对一个查询而言的,衡量该查询下所有相关文档在排序中的整体表现。
直观理解:AP 是“在每个相关文档被检索到时”的精确率的平均值。
公式定义: $$ AP = \frac{\sum_{k=1}^{n} (P(k) \times \text{rel}(k))}{\text{总相关文档数}} $$
其中: - $ P(k) $:在第 $ k $ 个位置的精确率(即前 k 个结果中有多少是相关的) - $ (k) $:第 $ k $ 个文档是否相关(1 表示相关,0 表示不相关)
也就是说,只在相关文档出现的位置计算并累加精确率,最后除以总相关文档数。
平均精确率均值(MAP)
将所有查询的 AP 求平均:
$$ MAP = \frac{1}{|Q|} \sum_{i=1}^{|Q|} AP_i $$
其中: - $ |Q| $:查询总数 - $ AP_i $:第 $ i $ 个查询的平均精确率

归一化折损累积增益(Normalized Discounted Cumulative Gain, nDCG)
nDCG 的核心思想是: 1. 高相关性的文档更有价值 2. 排在前面的结果比排在后面的价值更高(位置越靠前,权重越大) 3. 将系统的得分与“理想排序”对比,进行归一化,便于跨查询比较
1.累积增益(Cumulative Gain, CG)
CG 是前 $ k $ 个结果的相关性评分之和,不考虑位置。
$$ CG@k = \sum_{i=1}^{k} rel_i $$
其中 $ rel_i $ 是第 $ i $ 个文档的相关性评分。
❌ 缺点:CG 不关心排序顺序。无论相关文档排第1还是第10,CG 都一样。
- 折损累积增益(Discounted Cumulative Gain, DCG)
DCG 引入“位置折损”:越靠后的结果,其贡献被“打折”。
常用公式(两种形式,第二种更常见):
$$ DCG@k = \sum_{i=1}^{k} \frac{rel_i}{\log_2(i+1)} \quad \text{或} $$
$$ DCG@k = rel_1 + \sum_{i=2}^{k} \frac{rel_i}{\log_2(i)} \quad \text{(更常用)} $$
💡 解释:第1个位置不打折,第2个位置除以 $ _2(2) = 1 $,第3个位置除以 $ _2(3) $,相当于打了约 63% 的折扣。
这样,相关文档越早出现,DCG 越高。
- 理想折损累积增益(Ideal DCG, IDCG)
IDCG 是在理想排序下(所有相关文档按相关性从高到低排列)的 DCG 值。
IDCG@k = 将前 k 个最相关文档按最优顺序排列时的 DCG
IDCG 是当前查询下 DCG 的理论最大值。
- 归一化折损累积增益(nDCG@k)
$$ nDCG@k = \frac{DCG@k}{IDCG@k} $$
✅ nDCG 的取值范围是 [0, 1]: - 1.0:排序完全理想 - 接近 1:排序质量高 - 接近 0:排序很差

利用RAGAS评估rag性能
learn-rag-langchain/RAGAS-langchian.ipynb at main · zxj-2023/learn-rag-langchain
检索器 1.Contextprecision(上下文精确度):评估检索质量。 2.Context Recall(上下文召回率):衡量检索的完整性。 生成器 1.Faithfulness(忠实度):衡量生成答案中的幻觉情况。 2.AnswerRelevance(答案相关性):衡量答案对问题的直接性(紧扣问题的核心)。
最终的RAGAS得分是以上各个指标得分的调和平均值。简而言之,这些指标用来综合评估 -个系统整体的性能。
RAG的构建
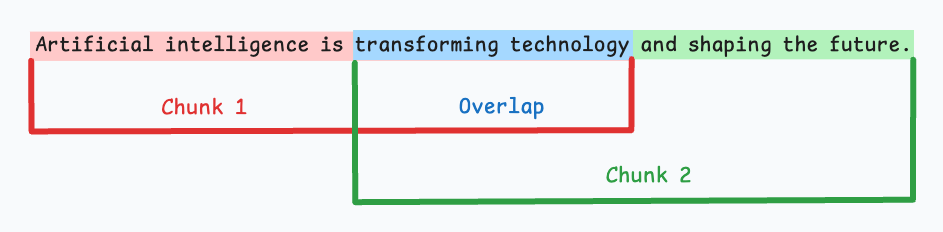
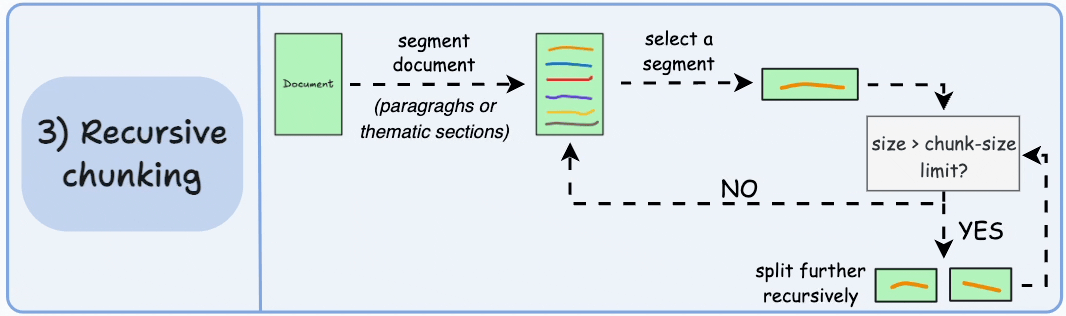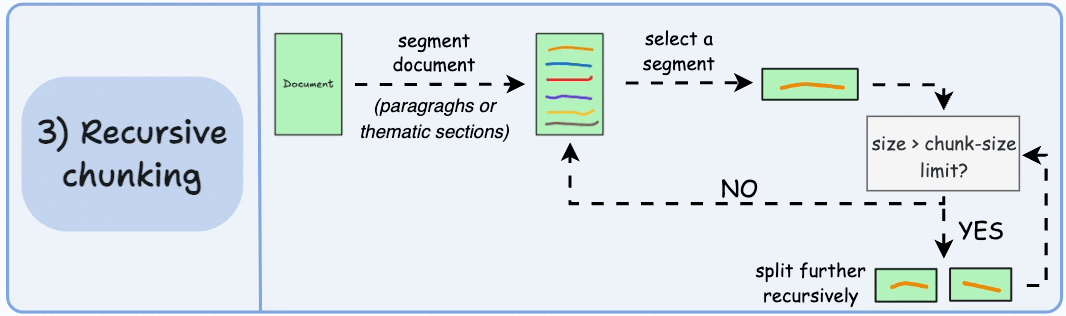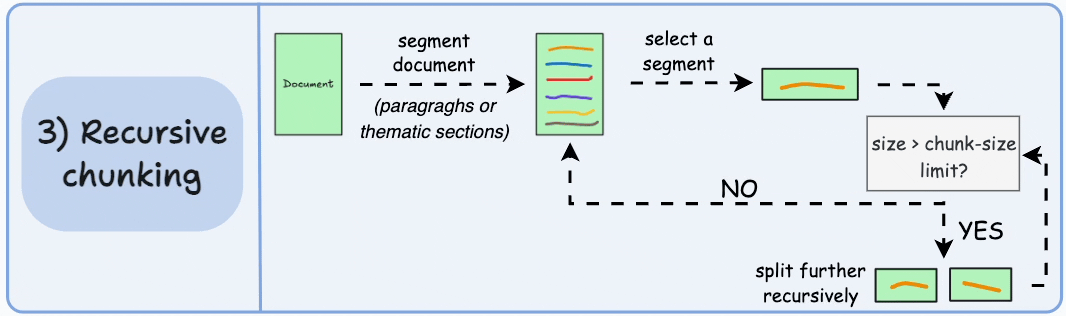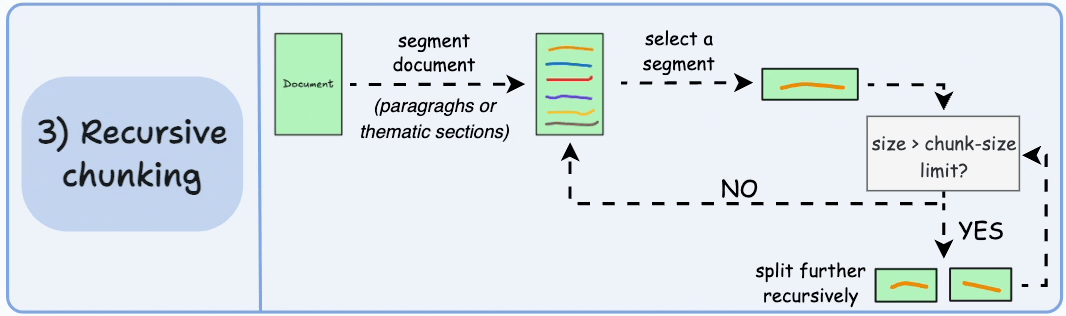
创建RAG文本分割、Embedding model 、 向量库存储Chroma
我们主要使用 RecursiveCharacterTextSplitter
切割文本,通过OpenAIEmbeddings()进行文本编码,存储到
VectorStore。
1 | from langchain.vectorstores import Chroma |
Chroma 向量数据库默认情况下是内存存储,这意味着数据在程序运行结束后不会保留。 但是,Chroma 也支持持久化存储,您可以指定一个路径将数据保存到磁盘上。这样,即使程序关闭,数据也会被保留,并在下次启动时自动加载。
检索器的构建
现在我们可以利用 Chroma 向量库的
.as_retriever() 方式进行检索,需要控制的主要参数为
k
1 | base_retriever = vectorstore.as_retriever(search_kwargs={"k" : 3}) |
- ectorstore.as_retriever() : 这个方法的作用是将一个向量数据库实例( vectorstore )转换为 LangChain 中的一个检索器( Retriever )对象。检索器是 LangChain 中负责根据用户查询从数据源中获取相关文档的核心组件。
- “k” : 这个键表示要检索的“最相似”文档的数量。在这里, “k” : 3 意味着当检索器接收到一个查询时,它将从向量存储中返回与该查询最相似的 3 个文档。这在 RAG(检索增强生成)系统中非常常见,用于限制传递给大型语言模型的上下文信息量,以提高效率和相关性。
检索器的作用 检索器(Retriever)是一个核心组件,其主要作用是从一个数据源(如向量数据库、文档加载器等)中根据给定的查询(query)检索出相关的文档或信息。
prompt的构建
我们需要利用LLM对Context
生成一系列的问题的answer
1 | from langchain import PromptTemplate |
生成answer,利用LLM
利用 Runnable 定义一个 chain
实现rag全流程。
1 | from langchain.schema.runnable import RunnablePassthrough |
创建 RAGAs 所需的数据
question Answer contexts ground_truths
1 | # Ragas 数据集格式要求 ['question', 'answer', 'contexts', 'ground_truths'] |
使用RAGAs 进行评估
1 | #将评估数据转换成 Ragas 框架专用的格式 。 |
我们可以使用一组常用的RAG评估指标,在收集的数据集上评估我们的RAG系统。您可以选择任何模型作为评估用LLM来进行评估。 ragas默认使用openai的api
1 | from ragas.llms import LangchainLLMWrapper |
调用
1 | from ragas.metrics import LLMContextRecall, Faithfulness, FactualCorrectness |

查看结果
1 | import pandas as pd |
参考资料
RAG系统效果难评?2025年必备的RAG评估框架与工具详解 - 知乎
如何利用RAGAs评估RAG系统的好坏_哔哩哔哩_bilibili
ragas中文文档Evaluate a simple RAG - Ragas
人工智能 - RAG系统的7个检索指标:信息检索任务准确性评估指南 - deephub - SegmentFault 思否